原子スペクトル（読み）ゲンシスペクトル

デジタル大辞泉

げんし‐スペクトル【原子スペクトル】

原子状態にある気体を高温に熱したときに、原子が放出または吸収するスペクトル。多くは線スペクトル。

出典　小学館

精選版 日本国語大辞典

げんし‐スペクトル【原子スペクトル】

1. 〘 名詞 〙 ( スペクトルは[フランス語] spectre ) 原子のもつ電子のエネルギー状態の変化にともなう光の吸収や発光。主として気体状の中性原子の与えるものをさし、波長幅が狭い。元素の同定や定量に利用する。〔自然科学的世界像（1938）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

原子スペクトル (げんしスペクトル)
atomic spectrum

原子の発する光および原子の吸収する光のスペクトル。線スペクトルと連続スペクトルとからなるが，ふつう原子スペクトルというと線スペクトルの部分を指す。

　気体に光をあてると，気体中の原子によって特定の波長の光が吸収され，スペクトルに暗線が現れる。1813年ごろJ.フラウンホーファーは太陽光スペクトルの中にある暗線を観察し，おのおのの色の中で代表的なものを選んで，A，B，C，D，E，F，G，Hと名づけた。この太陽光スペクトルの暗線はその後フラウンホーファー線と呼ばれるようになり，今日の知識によれば，これらの暗線は太陽内部から発せられる光が，太陽周辺部および地球の大気を通過する際に，気体中の原子によって特定の波長の光が吸収されることによって生ずるものである。原子が発する光と原子が吸収する光とは，一般に波長が等しい。

水素原子のスペクトル

85年に，J.J.バルマーは水素原子の発する光のスペクトルの中のH_α（波長6563Å，赤），H_β（4861Å，青），H_γ（4340Å，青紫），H_δ（4102Å，紫）の4本の線スペクトルの示す波長λがλ＝Am²/（m²－4）（m＝3，4，5，6，Aは定数）で表されることを発見した。これらの線スペクトルの系列はバルマー系列と呼ばれるが，その後，T.ライマンによって紫外部に，また，L.C.H.F.パッシェンによって赤外部に，それぞれラインマン系列，パッシェン系列と呼ばれる線スペクトルの系列が発見され，バルマー系列を含めて，これらの系列の線スペクトルの波長λは，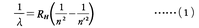

で表されることが明らかとなった。ただし，R_hは定数，n，n′は整数である。

その他の原子のスペクトル

J.R.リュードベリはアルカリ金属原子の線スペクトルのデータを整理して，線スペクトルの波長λが，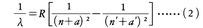

という式で表されることを示した。ただし，R，a，a′は定数，n，n′は整数で，a，a′には何通りかの値がある。Rと前出のR_hとはほぼ等しく，これらはリュードベリ定数と呼ばれる。スイスのW.リッツは，一般に原子スペクトルの光の振動数νが二つの項T_n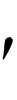，T_nの差としてν＝T_n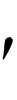－T_nの形に表されることを発見した。これはリッツの結合則と呼ばれる。光速度をcとすると，光の振動数νと波長λとの間にはν＝c/λの関係があるので，上に示した（1），（2）の二つの式はリッツの結合則の例となっている。

原子スペクトルと原子構造

バルマー，リュードベリ，リッツらによって得られた式が，原子の構造について何を意味するのかは長い間解明されなかったが，1913年にN.H.D.ボーアは画期的な水素原子模型を提案し，この問題を解決に導いた。ボーアの理論によると，水素原子内の電子は陽子（水素原子核）のまわりに等速円運動を行い，その角運動量がħ（ħ＝h/2π。hはプランク定数）の整数倍でなければならない。角運動量がnħの状態のエネルギーは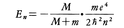，となる。ただし，mは電子の質量，Mは陽子の質量，eは陽子の電荷（電子の電荷は－e）で，nは主量子数と呼ばれ，n＝1，2，3，……のとびとびの値をとる。主量子数n′の状態からnの状態（ただしn′＞nとする）に移るときに放出される光の振動数νは，hν＝E_n－E_nによって定まるので，波長λを与える式は，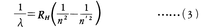

となり，定数R_hは，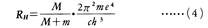

と表される。（3）式は実験的に知られていたものと一致している。すなわち，実験によるとR_h＝10967759m⁻¹であるが，これは（4）式から計算される値と一致する。

　ボーアの理論が成功を収めた後に，水素原子のスペクトル系列にブラケット系列，プント系列の2系列が発見され，これらもボーアの理論とあうことが確かめられた。まとめると，水素原子のスペクトルは次のようになる。ラインマン系列（紫外部）n＝1，n′＝2，3，4，……，バルマー系列（可視部～紫外部）n＝2，n′＝3，4，5，……，パッシェン系列（赤外部）n＝3，n′＝4，5，6，……，ブラケット系列（赤外部）n＝4，n′＝5，6，7，……，プント系列（赤外部）n＝5，n′＝6，7，8，……で，ただし，n′，nは光の放出の前後の主量子数である。

　アルカリ金属原子は閉殻の外に1個の電子が存在しているので，水素原子と類似しているが，主量子数nのほかにもう一つの量子数lを考えないとそのスペクトルは説明できない。換言すると，円軌道のほかに楕円軌道を考えることが必要である。ここで，nは軌道の円あるいは楕円の大きさを表す量子数であり，lは角運動量量子数である。おのおののn，lの組に対して一つのエネルギー準位が存在し，nl準位のエネルギーは－Rch/（n＋a）²という式で近似的に表され，aはlによって定まる。線スペクトルの波長は前出の（2）式で表される。アルカリ金属原子などのスペクトル系列については，鋭系列sharp series，主系列principal series，鈍系列diffuse seriesなどへの分類が行われたことがあり，このsharp，principal，diffuseの頭文字s，p，dが，l＝0，1，2を表す記号として用いられるようになった。その後この分類は適切でないことがわかったが，s，p，d，……でl＝0，1，2，……を表す慣行はそのまま残った。

　ボーアの理論によりリッツの結合則の意味も明らかになった。すなわち，リッツの結合則におけるT_nは原子のエネルギー準位のエネルギーE_nの1/hを意味する。

　なお，原子が電子を放出してイオンになる過程およびその逆の過程においては，外の電子のエネルギーは任意の値をとり得るから，吸収，放出される光は連続スペクトルになる。
→原子
執筆者：伊藤 敬

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

原子スペクトル
げんしすぺくとる

原子が放射または吸収する光のスペクトル。太陽の光をガラスのプリズムを通して白い紙に当てると、虹(にじ)のような七色が見える。ニュートンはこれにスペクトルという名を与え、太陽の光は種々の色の光が混じったものであることを初めて明らかにした（1670ころ）。高温の気体から放射される光はとびとびの波長をもった単色光からなり、これを分光器を使って波長に対して分散させると、元素の種類に特有の輝線スペクトルが観察される。これと逆に、連続スペクトルをもつ光を試料元素中に通すと、その元素に固有の波長の光だけが吸収されて暗線を生じ、吸収線スペクトルを示す。これらの線スペクトルは、元素の種類に応じ、その線間隔と強度が完全な規則性をもって並んでおり、スペクトル系列を形づくる。スペクトル系列の研究は19世紀の終わりから20世紀の初めにかけて盛んに行われ、原子構造の解明と量子物理学の発展に重要な役割を果たした。

　バルマーは、水素原子の可視部に現れる4本の輝線の波長λ(ラムダ)が、定数Gと正の整数mのみで表される簡単な式で精度よく再現できることをみいだした（1885）。

　　λ＝G・m²/(m²－4)
ここでGは3645.6×10^-8センチメートル、mは4本の輝線に対して3、4、5、6を代入する。後にリュードベリは、波長の逆数（波数）をとると、この式がより一般的な形で表されることを示した（1889）。

　　1/λ＝R(1/n²－1/m²)，（n＜m）
ただし、nは正の整数、Rはリュードベリ定数を表し、R＝4/Gである。これは今日バルマーの公式とよばれるものである。バルマーが最初にみいだした式は、このバルマーの公式においてn＝2とした特別な場合である。n＝2の系列はバルマー系列とよばれるが、m＞7に相当する輝線もその後の観測により発見され、バルマーの公式と高い精度で一致することが確認された。また、n＝1に相当する極紫外部の系列（ライマン系列）やn＝3に相当する赤外部の系列（パッシェン系列）の存在も後の観測により確かめられた。バルマーの公式は水素原子のスペクトル線の波数が項R/n²の差で表されることを示しているが、水素原子に限らずスペクトル線の波数は二つのスペクトル項Tの差で与えられる（リッツの結合原理）。

　　1/λ＝T_n－T_m
　水素原子の場合にはT_n＝R/n²であり、nは正の整数（主量子数）である。多電子原子の場合にはT_n＝R/n_e²でn_e（有効量子数）は整数からすこし外れてくる。主量子数と有効量子数との差は量子欠損とよばれる。バルマーの公式に量子欠損を取り入れ、多電子原子にも適用できる形にしたものをリュードベリの公式とよぶ。

　スペクトル項が実は原子のエネルギー準位を表すものであることを初めて明らかにしたのはボーアである（1913）。ボーアは古典量子論を用いてエネルギー準位を計算し、エネルギー準位間の遷移という考えを適用して、水素原子に関するスペクトルを説明した。その後、量子力学が確立して以後は、複雑な原子のスペクトルに関する解釈も完全に行われるようになった。スペクトル項に名前をつけるため、普通4通りの量子数の組を使い、これを一つの記号で表す。すなわち、主量子数nでだいたいのエネルギーが決まり、軌道角運動量を表す方位量子数L、スピン角運動量の量子数S、軌道とスピンを合成した内部量子数Jなどで準位の微細構造が決まる。L＝0, 1, 2,……の項を表すのにそれぞれS、P、Dなどの記号を使う。また2S＋1を多重度とよぶ。S＝0, 1/2, 1,……の項はそれぞれ一重項、二重項、三重項である。項の記号は、以上をまとめて、n^2s＋1L_Jの形に書く。たとえばn＝2, L＝0, S＝1/2, J＝1/2なら2²S_1/2となり、n＝3, L＝1, S＝1, J＝2なら3³P₂となる。

　光の吸収または放射によってどの項の間にも遷移がおこりうるかというと、そうではない。光学的遷移には選択則があって、選択則を満たす遷移（許容遷移）だけがおこりうる。方位量子数に関しては量子数Lの変化が±1だけの遷移が許される。またスピンSの変化を伴う遷移は禁じられている。

　スペクトル項はまた原子核の磁気モーメントの影響でいくつかの副項に分岐することがある。これを超微細構造とよぶ。水素原子メーザーは、水素原子の基底状態の超微細構造準位の間の遷移を利用してマイクロ波を発振する装置である。原子スペクトルは今日では、元素分析やレーザーに応用されるほか、太陽や星の研究に重要な役割を果たしている。

　プリズムや回折格子をレンズや球面鏡と組み合わせた通常の分光実験法を用いて観測された原子スペクトルの実験結果は、1940年代のなかばごろまでにすべて量子力学によって説明されるようになったが、その後開発された精密分光技術によって、原子スペクトルの研究は量子電磁力学や場の量子理論の対象となる物理学の基本問題の研究に適用されるようになった。1947年ラムとレザフォードRobert Curtis Retherford（1912―1981）は2S_1/2状態に励起(れいき)された水素原子の原子ビームを使いマイクロ波磁気共鳴法に基づいて2P_1/2状態との間にエネルギー差があることを発見し、その値を測定した。このエネルギー差はラム・シフトとよばれ、その値は2S_1/2状態の励起エネルギーの100万分の1程度にすぎないが、場の量子論の解明のためには重要な知見であり（1955年ラムはノーベル物理学賞を受賞）、まもなく朝永振一郎(ともながしんいちろう)、シュウィンガー、ファインマンらによって理論的に説明され（1965年3人は共同でノーベル物理学賞を受賞）、量子電磁力学の進歩に大きな貢献を果たした。その後、ラムゼー、デーメルト、パウルらは原子ビーム法、イオン・トラップ法と各種の共鳴法を組み合わせた分光技術を開発して、精密原子分光学の進歩に貢献した（1989年3人同時にノーベル物理学賞を受賞）。今日ではレーザー技術の発展とともに、光コム、光格子などの新しい技術が精密分光に導入され、極限的な精密測定が行われるようになった。そのような精密原子分光技術は、基礎物理実験のほか、原子時計の安定性向上などにも応用されている。

［鈴木　洋・中村信行　2015年9月15日］

[参照項目] | エネルギー準位 | 原子 | スペクトル | バルマー | ボーア | リッツの結合原理 | リュードベリ定数 | 量子電磁力学

出典　小学館　日本大百科全書(ニッポニカ)

化学辞典 第2版

原子スペクトル
ゲンシスペクトル
atomic spectrum

原子内の電子がその定常状態間に遷移を起こすことによって放出，または吸収する光のスペクトル．通常は線スペクトルであるが，連続スペクトルを生じる場合もある．スペクトル線の波数は，その遷移にかかわる二つのエネルギー準位に対応する二つのスペクトル項の差として与えられ，各スペクトル項は電子系内での相互作用の状態によって，適当な量子数により指定される．もっとも一般的に起こるラッセル-ソーンダーズ結合の場合には，全軌道角運動量量子数Lを表すS，P，D，Fなどの記号の左肩にスピン多重度 2S ＋ 1の値をつけて ²P，³S のように表す．また一重項以外では，内量子数Jの異なる微細構造を伴い，Jの値を右下につけて ²P_3/2，³S₁ のように表すこともある．これらの項(準位)間の双極子遷移の選択律は

ΔL ＝ 0，±1；ΔS ＝ 0；ΔJ ＝ 0，±1
およびラポルテの規則で与えられる．重い原子などでラッセル-ソーンダーズ結合が成立せず，j-j結合が適用される場合には，選択律は

ΔJ ＝ 0，±1；Δ j_i ＝ 0，±1
となる( j_i は個々の電子の内量子数)．一般に観測されるのは外殻電子1個の遷移によるもので，それらのスペクトル線の波数は，遷移電子が占める軌道の主量子数nがとりうる種々の値に対応した系列をつくっている．それらの系列は，J.R. Rydbergが与えた次の近似式により統一的に表されることが知られている．

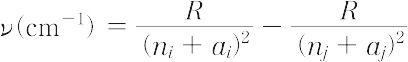
ここで，Rはリュードベリ定数，n_i，n_j は主量子数，a_i，a_j( ＜ 1)は各項に固有のリュードベリ補正項である．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

原子スペクトル
げんしスペクトル
atomic spectrum

自由な状態にある原子が放射または吸収する光のスペクトル。原子スペクトルは特殊な場合を除いてはスペクトル写真の上で線状のスペクトルを示すので線スペクトルともいう。原子が光を放射，吸収するのは原子核のまわりを周回運動している電子のエネルギー状態が変化することに対応している (→リッツの結合原理 ) 。そのような電子のエネルギー状態は各元素に固有であるので，原子スペクトルを調べることで，どの元素の，どのようなエネルギー状態の変化が起きたかを知ることができる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

原子スペクトル【げんしスペクトル】

→線スペクトル

出典　株式会社平凡社

世界大百科事典（旧版）内の原子スペクトルの言及

【光スペクトル】より

…また連続スペクトルをもつ光が物質を通過したとき，その物質に特有な波長領域が吸収されて欠けるか弱められたものを吸収スペクトルといい，これに対して，物質から放出される光のスペクトルを発光スペクトルまたは放射スペクトルという。　原子が放出または吸収する光のスペクトルを原子スペクトルといい，一般には線スペクトルである。原子や固体中のイオンの電子状態の間の遷移に対応するスペクトル線はおもに可視から紫外の領域に現れ，励起状態の間の遷移は赤外領域にも現れる。…

※「原子スペクトル」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」