構造力学（読み）コウゾウリキガク（英語表記）structural mechanics

デジタル大辞泉

こうぞう‐りきがく〔コウザウ‐〕【構造力学】

機械や建造物などを構成する各部材に生ずる応力や変形を計算し、適切な材質や形状、寸法の決定法を研究する学問。

出典　小学館

精選版 日本国語大辞典

こうぞう‐りきがくコウザウ‥【構造力学】

1. 〘 名詞 〙 応用力学の分野の一つ。建築物、橋梁、高架道路、船舶、機械などの構造物に加わる外力や荷重が、構造物の各部または全体にどのように作用するかを調査し、それに対する応力や変形を計算して、構造物の総合的な安全度を算定する学問。構造解析学。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

構造力学
こうぞうりきがく
structural mechanics

建物、橋、ダム、航空機、船舶、機械など、種々の形状の要素で構成され、全体として所要の力学的機能を果たすようにつくられた物体を構造物といい、構造物が地震、風、雪、波浪などの外的攪乱(かくらん)や、機能に応じた外力の作用を受けたときに示す挙動を予測する力学理論を構造力学という。

［中村恒善］

梁の理論

構造物はその目的に適合する形状と大きさでつくられる。たとえば、川や谷を横切って、人や車両に平坦(へいたん)な通行路を提供するために橋がつくられる。橋の原始的な形状は1本の丸木橋であり、橋として川や谷を横切るのに必要な長さをもち、材軸線がほぼ直線で、その上を移動する物体の重量を支持できるような太さをもつ棒材が選ばれる。このような棒材を梁(はり)といい、梁の理論は材料力学や構造力学の基礎理論である。梁の理論は、まず変形前の材軸線に垂直な1対の仮想切断面で切り出される梁の要素が、変形後には、変形後の材軸線に垂直な1対の平面をもつ扇型要素に移行するという第一近似（平面保持の仮定という）に基づいて構成される。梁要素の曲げ変形は扇形要素の角θで代表される。このような各梁要素の仮想切断面には隣接要素との間の力学的相互作用が働いている。切断面に垂直な方向の成分を垂直応力、切断面に沿う方向の成分を剪断(せんだん)応力という。このように分布する相互作用の合力および合モーメントを総称して合応力または断面力という。梁の支配式は、材軸線上の点に属する断面力と要素変形量（θ）の間の関係式（材料法則）、断面力と要素に作用する外力との間のつり合い式、および材軸線上の点の変位と要素変形量の間の関係式の3種類の式で構成される連立常微分方程式の系となる。このように、支配式のすべての変量が材軸線上の点に属する量のみに帰せられるので、梁は理論上は、あたかも線材のようにみなされたことになる。

［中村恒善］

骨組の理論

多種多数の棒材を組み合わせ、接合することによって構成される構造物を骨組という。後述の平板要素と組み合わせられた骨組を有壁骨組、または単に骨組という。構成要素の梁があたかも線材として取り扱われるのに対応して、骨組もまた第一近似としては、線材と線材とが力学的性能を有する点（節点という）で理想的に接合されたものとして扱われる。

　骨組の力学は、その要素棒材（部材という）の挙動を記述する式に基づいて構成される。部材の挙動は、その線材としての材端に作用する材端力、材端モーメントと、材端変位、材端回転角の間の関係式で記述される。これを部材剛性関係式という。1個の骨組の各部材の部材剛性関係式に、節点での接合条件と、節点まわりの自由体についての材端力と外力の間のつり合い式とを用いると、その骨組全体についての剛性関係式が導かれ、それにその骨組の支持条件を課すると、与えられた外力の下でのその骨組の挙動を記述する連立方程式が導かれる
　構造物の挙動解析は、その構造設計の基礎となる。1個の骨組の構造設計に際しては、その完成後の所定年限に作用すると想定される最悪のまたは最大レベルの外的攪乱を評価し、そのような外的攪乱が骨組に作用した場合の力学的挙動を解析することによって、その骨組が所要の力学的性能を保有することを検定、照査する。たとえば建築骨組の場合、設計用荷重を法令の規定に従って算出し、その作用の下における骨組の力学的挙動を解析し、その結果が安全性に関する規定を満たすかどうか検定することになる。

［中村恒善］

板構造の理論

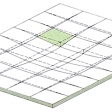
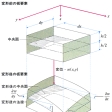
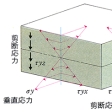
建築骨組は、一般に骨組のみならず壁や床板のような平板状の要素も含んでいる。壁や床板は、建築計画上の機能を果たすのみならず、力学的機能も果たす。1枚の平板や、その組合せでつくられる箱状構造物の力学もまた構造力学の一分野である。平板の力学的機能は2種類ある。平板はその板面に沿う方向の外力に対して高い剛性を示す。建築骨組の中の壁は、水平力による骨組の変形と床の水平変位を抑制するのに役だてられる。これに対して、床板は、第一に板面に垂直な方向の自重や積載荷重を支持し、第二にその高い面内剛性に応じて多数の並列平面骨組を連結し、それらの外力に対する抵抗作用を一体化する、という2種類の役割を果たす。図Aには、長方形平板が板面に垂直な荷重の作用を受けて曲げられる場合の変形曲面の略図を示した。図Bの上図のように、変形前の平板中に、板面に垂直でかつ互いに垂直な2対の平行平面で想像上切り出される板要素を考えることができる。その変形後の形（図Bの下図）は、2方向に扇型であるような曲げ変形と、ねじれ変形との重ね合わせとして記述できる。また、図Cのように、2対の相対する断面には垂直応力や剪断応力が作用していて、合力と合モーメントをもっている。平板要素の力学的および幾何学的状態は、図B上図の平板中央面上の点に属する変位量、変形量および断面力によって記述される。平板の支配式は、板要素の断面力‐変形量関係式、変位‐変形量関係式およびつり合い式で構成され、一般には偏微分方程式の系となる。

　シェル構造の力学も平板の力学と類似の考え方で構成される。ドーム型シェル構造では、アーチ作用とたが作用の複合効果によって作用荷重が支持される。これに対して、縁梁をもつくら型シェル構造では、吊(つ)りケーブル作用と押さえケーブル作用の複合によって荷重が支持される。シェル構造の挙動解析、崩壊過程解析も構造力学の一分野である。

［中村恒善］

『中村恒善著『建築骨組の最適設計』（1980・丸善）』▽『中村恒善編著『建築構造力学図説・演習Ⅰ・Ⅱ』（1982・丸善）』▽『佐藤稔夫・中村恒善著『新建築学大系36　骨組構造の解析』（1982・彰国社）』▽『日置興一郎著『構造力学Ⅱ』（1977・朝倉書店）』

[参照項目] | シェル構造 | 梁

変形曲面の略図〔図A〕

変形前後の板要素〔図B〕

板要素の断面に作用する応力〔図C〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

構造力学 (こうぞうりきがく)
structural mechanics

建物，橋，高架道路，あるいは船や飛行機などの構造物に外力が作用するとき，構造物の各部分に生ずる応力と変形を解析する学問。応用力学の一部門であり，構造解析学と呼ばれることもある。単一部材に生ずる応力と変形を対象とする材料力学を基本として成立しており，両者はいちおう区別されているが密接な関係にある。構造力学で取り扱う構造物は，主としてラーメン，トラスなどの骨組構造で，平面板や曲面板で構成される構造物や地盤のように三次元的に連続した物体は，ふつう弾性学（弾性論）の対象とされている。

　構造力学の直接の対象物は，構造物を理想化したモデルである。モデルは構造物の実際の力学的挙動を工学的に反映し，かつできるかぎり単純化し理想化することが望ましい。建物などの構造体は表面から見えないことが多いので，そのモデル化にはある程度の経験が必要である。構造物のモデルに作用させる外力は，設計荷重または設計外力と呼ばれ，法規や規準類に必要最低限の値が決められていることが多い。構造解析で求まった応力に対し構造物の各部材の設計をし，また変形が許容限度以内におさまっているか検討する。このような部材の設計までも構造力学に含めることもあるが，ふつうこの部分は材料力学の分野とされ，木構造，鉄筋コンクリート構造，鉄骨構造など構造材料の種別ごとに固有の学問体系があって，設計規準類も整備されている。

　構造力学の発達は，その対象物である構造物の発達の歴史と不可分の関係にある。例えば，トラスの理論は19世紀中ごろ，S.ホイップル，D.J.ジュロースキー，K.クルマンらによって発展し，錬鉄や鋼による大スパンのトラス橋の建設を可能にした。またラーメンの理論は20世紀初頭にA.ベンディクセン，W.M.ウィルソン，H.クロスらによって開発され，鉄筋コンクリートによる連続一体化した構造体の発達と普及を促進した。構造力学では，ふつう構造物が線形挙動をすると仮定する。線形挙動とは，すべての応力と変形が外力の一次関数で表されるということである。実際の構造物では，線形性は次の三つの原因によって近似的にしか成立しない。第1は材料の非線形挙動であり，線形構造解析では材料の応力が小さい範囲にあると仮定しているが，構造物の破壊を対象とする終局強度理論では材料の非線形性は無視できない。第2は幾何学的非線形といわれるもので，構造物の変形が部材の寸法に比べて大きくなると，変形を考慮してつり合い条件を立てなければならないが，線形解析では変形が微小であるとして変形前の構造物の幾何学的形状に基づいてつり合い式を書いている。第3は軸方向力と曲げ変形との相関で，理論的には第2の原因の特別の場合であるが，実際問題としてはきわめて重要である。軸方向圧縮力が大きくなると，部材の変形様式がそれ以前とは急激に変化する座屈（曲げ座屈）と呼ばれる現象が発生するが，線形解析では軸方向力による曲げ変形の増減を無視している。線形性を仮定するのは，構造解析を連立一次方程式によって行うことができ，また解の重ね合せが可能になるという実用上きわめて大きな利点が生ずるためで，非線形挙動を扱う構造力学では，反復計算による逐次近似法を用いるか，あるいは微小増分について線形性を仮定する増分解析法を用いて解析を行う。
→骨組構造
執筆者：青山 博之

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

構造力学【こうぞうりきがく】

構造解析学。工学の基礎部門の一つ。建物，橋，機体，船体などの構造物について，構造の強さや安定，各部材の受ける力，変形，破壊などを解析する学問。立体構造を形成する構造要素としての梁(はり)，柱，トラス，ラーメン，アーチなども重要な対象。材料力学，弾性論，振動論などと密接に関連している。
→関連項目材料力学｜土木工学

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

構造力学
こうぞうりきがく
structural mechanics; theory of structures

力学を応用して，建築物，橋梁，高架道路，船舶，航空機など構造物の構造的な安全性を評価したり，あるいは，これらを設計するにあたり必要な解析を研究する工学の一部門。一般的には，構造物の形状を研究したり，構造物に作用する種々の荷重を与えて構造物の変形や応力状態を決定する学問で，近年コンピュータの発展により，種々の汎用解析プログラムが開発されている。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の構造力学の言及

【材料力学】より

…これは，固体の運動方程式，変形の幾何学的性質を示すひずみと変位の式などを，与えられた力学的･幾何学的境界条件の下で解くことにより，物体内の応力とひずみを求めるものであって，固体力学とも呼ばれている。取り扱う材料の力学的性質によって弾性学，塑性学，粘弾性学，クリープ力学などに分けられ，また形状や力の加わり方の特徴に着目して，物体を棒，はり，板，殻などのモデルに近似し応力を求める構造力学は実用上重要であり，歴史的にみた場合材料力学はこれから出発したといえる。近年ではコンピューターの発達に伴って有限要素法などによる数値応力解析法が実用上有力な方法となっているが，理論的･数値的解法以外にも，ひずみゲージ法，光弾性法，モワレ法，応力塗料，X線回折法などによる実験応力解析法も用いられる。…

※「構造力学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」