SU対称性（読み）エスユーさんたいしょうせい（英語表記）SU（3）symmetry

改訂新版　世界大百科事典

SU（3）対称性 (エスユーさんたいしょうせい)
SU（3）symmetry

SU（3）対称性とは，一般に3種類の複素数量があったとき（物理学の場合は3種類の波動関数），その三つの量の間の一次変換の中でとくに行列式の価が＋1になるようなユニタリ変換を考え，その変換のもとで理論の中にでてくる方程式がすべて不変であるような性質をいう。素粒子論では強い相互作用をするあらゆる素粒子は陽子（P），中性子（N），ラムダ粒子（Λ）の三つの素粒子からできているとする坂田模型を数学的な理論体系に築きあげる過程で，日本の池田峰夫，小川修三，大貫義郎およびアメリカのM.ゲル・マンらによって導入された。池田，小川，大貫の理論では坂田にならって基本粒子をP，N，Λの三つとし，理論はこの三つの粒子の波動関数の任意のユニタリな一次変換に関して不変になっているとするもので，これは正確には三次元ユニタリ群（U（3）群）の変換に対して対称な理論であった（U（3）対称性）。これに対してゲル・マンの理論ではP，N，Λおよび同じくスピン1/2のシグマ粒子（Σ⁺，Σ⁻，Σ⁰），グザイ粒子（Ξ⁰，Ξ⁻）の八つが三次元特殊ユニタリ群（SU（3）群）の八次元表現になっているとした（八道説eightfold way）点で多少相違する。SU（3）対称性の破れ方の規則性からゲル・マン=大久保の質量公式が導かれたが，この式はSU（3）の十次元表現に属するスピン3/2の粒子で，当時は未発見であったオメガ粒子（Ω⁻）の質量を予見し，1964年に予見どおりの質量のところにこの粒子が発見されたことによってSU（3）対称性の理論の正しさが証明された。スピン1/2の粒子を八次元表現にあてはめるゲル・マン流の考え方は，さらにSU（3）群の基本表現の三次元表現にあてはめるべき粒子としてu，d，sの三つのクォークの存在の仮定に導き，すべての強い相互作用をする素粒子はいくつかのクォークからできていると考えられるようになった。その後クォークの存在が確定的なものとなり，現在ではゲル・マンの考え方のほうが，P，N，Λを基本粒子とする坂田らの考え方に比べ，現在までに知られているどのような実験事実とも矛盾を起こしていないという点でより有益であると信じられている。この考え方に従えば，SU（3）対称性は，強い相互作用を記述する理論が三つのクォークの波動関数の任意のユニタリな変換に関して不変であることを意味する。SU（3）対称性の実際的応用は，散乱振幅や崩壊振幅の間の関係式の導出や新しい共鳴状態の分類など非常に有力かつ広範囲である。ただし現在ではこのSU（3）対称性が近似的なゲージ対称性になっていないという意味で強い相互作用の基本的対称性であるとは考えられていない。
執筆者：菅原 寛孝

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

SU(3)対称性
エスユースリーたいしょうせい
SU(3) symmetry

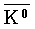アイソスピンとストレンジネスを同等に含む変換群 SU(3)に関する不変性。ユニタリ対称性の1種である。 SU(3)群は荷電空間を部分空間とする三次元複素空間（ユニタリ空間）内の変換群であり，強い相互作用は SU(3)群に関して近似的に不変である。これは u，d，s のクォークの質量差があまり大きくないことによる。ハドロンは SU(3)群の既約表現であるアイソスピン-ストレンジネス多重項によって分類される。各多重項は同一のスピン，パリティをもつ。たとえば，擬スカラー中間子の八重項（ π⁺ , π⁰ , π^- , K⁺ , K⁰ , , K^- , η ）および一重項（ η' ），ベクトル中間子の九重項（ K^*+，K^*0，ρ⁺，ρ⁰，ρ^-，K^*0，K^*-，ω，φ ），バリオン八重項（ p，n，Λ，Σ⁺，Σ⁰，Σ^-，Ξ⁰，Ξ^- ），バリオン十重項（ Δ⁺⁺，Δ⁺，Δ⁰，Δ^-，Σ^*+，Σ^*0，Σ^*-，Ξ^*0，Ξ^*-，Ω^- ）などの多重項が知られている。多重項に属する粒子の質量間には簡単な公式（ゲルマン＝大久保の質量公式）が成り立ち，ハドロン間の相互作用の強さの比も決定される。なおアイソスピンとストレンジネスに加えてチャームをも同等に含む変換群 SU(4)に関しても，強い相互作用は近似的に不変である。

SU(4)対称性
エスユーフォーたいしょうせい

「SU(3)対称性」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典