多様体（読み）タヨウタイ（英語表記）manifold

デジタル大辞泉

たよう‐たい〔タヤウ‐〕【多様体】

１ 《manifold》局所的にユークリッド空間とみなせる空間や図形を含む位相空間。多様体上では、いたる所に局所的な座標系を設けることができ、座標系が示す自由度がnである場合、n次元多様体という。
２ ⇒バリアント3

出典　小学館

改訂新版　世界大百科事典

多様体 (たようたい)
manifold

位相空間Mの各点pがn次元ユークリッド空間Rⁿと同相な近傍U（p）をもつとき，Mをn次元（位相）多様体という。U（p）からRⁿへの同相写像をf_pとするとき，U（p）とf_pの組（U（p），f_p）をpの局所座標系と呼ぶ。Mの異なる2点p，qの局所座標系を（U（p），f_p），（U（q），f_q）とするとき，U（p）とU（q）に共通部分U（p）∩U（q）が存在すれば，U（p）∩U（q）には二つの座標関数f_pとf_qが存在する。f_pの逆写像f_p⁻¹とf_qの合成写像f_q◦f_p⁻¹はRⁿの開集合f_p（U_p∩U_q）からRⁿの開集合f_q（U_p∩U_q）への写像であり，n個のn変数関数の組であるが，U_p∩U_qにおける二つの座標系f_pとf_qの間の座標変換を与えている。この座標変換が，U（p）とU（q）が交わる場合には，いつでもr回微分可能（0≦r≦∞）な関数であるとき，Mはr回微分可能多様体と呼ばれる。r＝0の場合には，座標変換は連続性のみしか要求されずつねに成立しており，この場合が位相多様体であり，座標変換に対する微分可能性の要求は位相多様体に一つの構造を与えるものと考えられ，微分可能構造ともいわれる。微分可能性のほかにも座標変換に種々の条件をつけることにより，一つの多様体に異なる構造が考えられるが，複素解析的多様体もその一例である。局所座標系を用いて種々の構造を多様体に定義するとき，座標変換で不変な構造であることが要求される。

　ユークリッド空間それ自身は多様体であるが，多様体の特徴は，空間全体を独立なn個の実数の組で1対1連続的に表示できない場合でも，いくつかの座標系を適当に組み合わせて空間全体を表示することができることである。例えば地球の表面は二次元球面Sと同相であるが，Sを1対1連続的に平面上に写像することはできない。しかし北極を除いた部分Uは北極から南極に接する平面に射影することにより平面上に1対1連続に写像できる。同様に南極を除いた部分Vにも座標系を入れることができる。Sは座標系をもつ部分UとVとでおおわれ，Sは二次元多様体と考えられる。二次元球面は3個の実数x，y，zの組の全体であるR³の中でx²＋y²＋z²－1＝0で定義される図形であるが，Rⁿの中でm個の独立な微分可能関数の零点からなる図形は（n－m）次元多様体になる。このような意味の多様体は，解析学の発展とともに18世紀以来考えられていたが，いくつかの座標系を組み合わせて抽象的に多様体を構成したのはB.リーマンである（1854）。多様体は幾何学の基本的研究対象であるのみならず，現代数学における一つの基本的概念と考えられている。
→位相幾何学
執筆者：田尾 鶉三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

多様体
たようたい

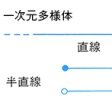
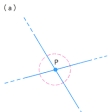
ユークリッド空間をモデルとした位相空間を多様体という。いちばん単純な図形は点であり、これは〇(れい)次元多様体という。線の図形のうち、左右無限に延びている直線、半直線、円周、線分が一次元多様体である（図A）。これに対して図Bのような線の図形は多様体ではない。すなわち、図Bで点Pの近傍、つまり点Pの近くにある点の集合が、(a)では十字形であり、(b)ではT字形であり、どちらにしろ線分ではないからである。

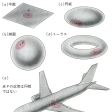
　面の図形は、その各点で、その近傍が円板と同位相になるものを二次元多様体という。図Cのような、平面や球面や円板やトーラス（輪環面）は様体であるが、球面に矩形(くけい)などを取り付けた(e)のような図形は、取り付けた点Pの近傍が円板でないので多様体ではない。各点の近傍が球体（つまり三次元球体）となるような三次元的図形が三次元多様体で、普通の三次元空間や三次元球体自身はそれぞれ三次元多様体である。同様に、各点の近傍がn次元球体となるようなn次元的図形をn次元多様体という。n次元空間やn次元球体はn次元多様体である。多様体は、平面や球面やトーラスのように境界のないものと、円板のように境界（円板はその円周が境界となる）をもつものとに分かれる。境界のない多様体の各点の近傍は球体からその境界を除いた開球体となる。よって境界のない二次元多様体上に近眼の虫がいると仮定すると、虫はどこにいても同じ開円板（境界の円周を省いた円板）、つまりいつも同じ景色を眺めていることになる。さらに球面やトーラスは空間の中で有限の大きさをもつ閉集合であり、閉じた多様体（二次元の場合、閉曲面）という。

　多様体が三角形分割できて多面体とみなせるとき、組合せ多様体といい、さらに多様体に微分構造が導入できるとき微分（可能）多様体という。

［野口　廣］

[参照項目] | 微分トポロジー

〇次元多様体と一次元多様体〔図A〕

多様体ではない線の図形〔図B〕

多様体の図形と多様体ではない図形〔図C…

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

多様体
たようたい
manifold

マニフォルド，集合体ともいう。幾何学的な類比を通じて，4次元以上の空間を研究するために導入された概念。点，直線，平面，円，三角形，立体，球などのような幾何学的図形の集合を一つの空間とみなしたときの，その空間のことをいう。たとえば平面上のすべての円から成る集合は，3次元多様体をつくるとか，現実の空間内のすべての球から成る集合は，4次元多様体をつくるとかいわれる。ここでいう多様体の次元は，それがいくつの数の組で定義されるかによって決る。円の全体が3次元多様体といわれるのは，円が，その中心の座標 (x，y) と半径 t との組，すなわち座標 (x，y，t) をもつ点としても表現されうるからである。空間・時間によって考えられた空間は，その対象を座標 (x，y，z，t) の点と考えれば4次元多様体ということになる。相対性理論が大きく進歩したのは，この4次元の時空多様体の概念が導入されてからである。現在では，微分可能な多様体を略して多様体と呼ぶことが多い。

出典　ブリタニカ国際大百科事典 小項目事典

知恵蔵

多様体

局所座標系を関数で貼り合わせてできる図形を、多様体という。例えば、提灯を作る時、竹などでできた枠に紙を貼って作る。紙の上に座標系を書いておけば、2枚の紙が重なる点は提灯の上では同じ点になり、2枚の紙の上の2点が貼り合わされる。この時、紙の上の座標系が局所座標系であり、できた提灯が多様体である。数学では、この貼り合わせを関数で行う。貼り合わせの関数が、連続関数の時は位相多様体、無限回微分可能の時は微分可能多様体、正則関数の時は複素多様体と呼ぶ。またいくつかのn変数多項式の共通零点を多項式関数で貼り合わせてできる多様体を、代数多様体という。19世紀中頃、リーマン(G.F.B.Riemann)がリーマン面を概念化したのが多様体の始まり。

(桂利行 東京大学大学院教授 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」

世界大百科事典（旧版）内の多様体の言及

【位相幾何学】より

…
［多様体］
　高次元の概念は19世紀中ごろすでに確立されていたが，高次元曲面の概念はリーマンによる。リーマンによる高次元曲面は20世紀前半において多様体manifoldとして定式化され，多様体は数学における一つの基本的図形とみなされ，その位相幾何学的研究は位相幾何学の一つの中心となっている。高次元多様体の位相構造はホモトピー論を通して代数的位相幾何学の研究に帰着する場合が多いが，三次元および四次元多様体の位相構造の研究は固有の困難さを伴っている。…

【位相幾何学】より

…基本群，一次元ホモロジー群は高次のホモトピー群，ホモロジー群に拡張されるが，さらに20世紀後半には，空間に対応させる代数的構造はますます多様化し精密化され，代数的位相幾何学は位相幾何学における基本的分野と考えられている。
［多様体］
　高次元の概念は19世紀中ごろすでに確立されていたが，高次元曲面の概念はリーマンによる。リーマンによる高次元曲面は20世紀前半において多様体manifoldとして定式化され，多様体は数学における一つの基本的図形とみなされ，その位相幾何学的研究は位相幾何学の一つの中心となっている。…

【広中平祐】より

…60年ハーバード大学大学院数学科を修了後，フランス高級科学研究所研究員，アメリカ･ブランダイス大学準教授，コロンビア大学教授を経て，68年ハーバード大学教授，76年京都大学教授となる。数学における業績は幅広いが，そのもっとも著しいものは多様体variety(代数的多様体，実および複素解析的多様体)の特異点解消問題の解決である。1967年朝日賞，70年日本学士院賞，フィールズ賞を受賞，75年文化勲章受章。…

※「多様体」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」