化学辞典 第2版 の解説
シュレーディンガーの波動方程式
シュレーディンガーノハドウホウテイシキ
Schrödinger wave equation
粒子運動に対する量子力学的な基本方程式.簡単のため1粒子系で説明すると,量子力学の公理によって粒子の全エネルギーに対応するハミルトニアンの固有値問題は,
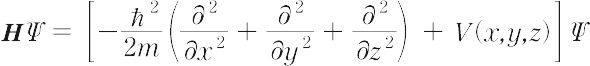
= EΨ
という二次の偏微分方程式となる.これをシュレーディンガー(1926年)の波動方程式といい,もっとも基本的な系のエネルギーに対して状態関数Ψを解くものである.Ψがx,y,zのほかに時間tを含んでいるとき,定常的な問題では,
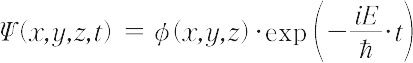
と書けて,エネルギー演算子を作用させると,
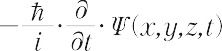
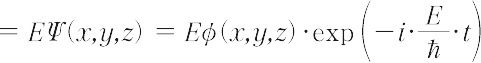
となるから,
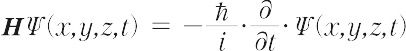
という時間を含んだシュレーディンガーの方程式も,結局,Ψをφ(x,y,z)に書き換えた波動方程式になる.別項の量子力学で述べたことを示すため,一次元の振動子の場合を扱ってみる.振動数をνとするとき,V(x)は2π 2 ν 2mx 2であるから,シュレーディンガーの波動方程式は,
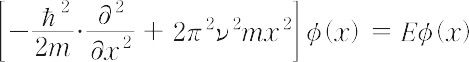
である.いま,
β = 2πνm/ℏ,ε = 2mE/ℏ2
として
ξ = 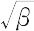 x
x
に変数を変換すると,
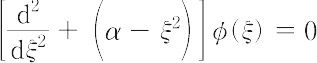
という方程式になる.ただし,α = ε/β.別項の固有値で示すように,φ(x)が2乗積分可能という条件,
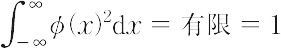
は,
α = 2λ + 1(λ = 0,1,2,…)
であればよい.この固有値条件は,
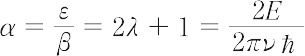
であるから,

であることになる.つまり,粒子が1個あるという条件のもとにシュレーディンガーの波動方程式を固有値問題として解くと,系のエネルギーEは,定数1/2を除いてプランクの量子条件と同じhνの正整数λ倍のみが可能であることがいえる.λの値に対して定まる関数 φ0(x),φ1(x),φ2(x),…を固有関数といい振動子の状態を表す.振動子に対する過渡的な前期量子論と量子力学の結果の相違は,零点エネルギーhν/2の有無にある.しかし,いろいろな点からみて,零点エネルギーが存在するほうが合理的であることがわかっている.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
日本大百科全書(ニッポニカ) の解説
シュレーディンガーの波動方程式
しゅれーでぃんがーのはどうほうていしき
シュレーディンガーが1926年に提出した、水素原子内電子の波動を記述する方程式。
電子のエネルギーはその位置座標xなど、運動量pxなどを用いて(px2+py2+pz2)/2m-e2/rで与えられる。ここでmは電子の質量、eは単位電荷、rは陽子からの距離である。シュレーディンガーの波動方程式は、pxなどを演算子-iħ∂/∂x(ħはプランク定数hの2π分の1)で置き換えたエネルギー演算子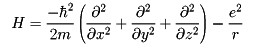
の固有方程式Hφ=Eφあるいは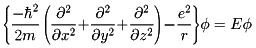
である。この場合、電子の波動の時間的変化もこのHを用いてiħ∂φ/∂t=Hφで与えられる。前者が時間に依存しないシュレーディンガー方程式、後者が時間に依存するシュレーディンガー方程式である。水素原子内電子の場合に限らず、一般に場や粒子のHの固有方程式、あるいはHを用いた波動関数の時間的変化を与える方程式をもシュレーディンガー方程式とよぶ。
シュレーディンガー方程式は、シュレーディンガーがド・ブローイの提唱した電子に伴う波動を、幾何光学の類推を用いてポテンシャルのある場合に拡張したものであるが、量子的状態を正しく与えるものであって、形式の相違はあってもハイゼンベルクの行列力学と同等であることが示されている。
また、座標に対する運動量は座標xの微分に-iħをかけて得られるが、これは運動量という物理量が座標系をx方向にずらしても不変であることから与えられる。エネルギー量に関しても、時間をずらしても不変であることから得られる。この方程式は量子的状態を記述する量子力学の基本的な式である。
[田中 一・加藤幾芳]
ブリタニカ国際大百科事典 小項目事典 の解説
シュレーディンガーの波動方程式
シュレーディンガーのはどうほうていしき
Schrödinger's wave equation
iℏ∂Ψ/∂t=HΨ
これをシュレーディンガーの波動方程式,またはシュレーディンガー方程式という。 ℏはディラック定数(h/2π,h はプランク定数)である。H はハミルトニアンと呼ばれ,系のエネルギーを表す演算子である。特に質量m の粒子がポテンシャルV(r)をもつ外力を受けている場合,古典力学における力学的エネルギーに対応して,H=-(ℏ2/2m)V2+V となる。なお,電子などを相対論的に扱わなければならないときは,ディラック方程式を用いなければならず,この方程式から導かれるスピンは重要な量である。したがって,非相対論的に扱う場合でも,スピンを考慮した波動方程式を用いなければならないことが多い。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
法則の辞典 の解説
シュレーディンガーの波動方程式【Schrödinger's wave equation】
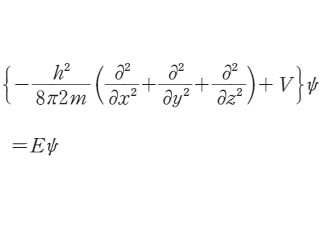
の解となる.よく略して Hψ=Eψの形で書かれる.
改訂新版 世界大百科事典 の解説
シュレーディンガーの波動方程式 (シュレーディンガーのはどうほうていしき)
→波動力学
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

