量子条件（読み）リョウシジョウケン

デジタル大辞泉

りょうし‐じょうけん〔リヤウシデウケン〕【量子条件】

古典量子論において、水素原子内の電子が安定的な軌道をとりうる条件。電子は特定の軌道しかとることができず、別の軌道に移るときには、エネルギー準位の差に相当するエネルギーの電磁波を吸収または放出しなければならない。ボーアが提唱し、のちにゾンマーフェルトが一般化した。ボーアの量子条件。ボーア・ゾンマーフェルトの量子条件。

出典　小学館

化学辞典 第2版

量子条件
リョウシジョウケン
quantum condition

量子論とくに前期量子論において，ある物理量の量子性とプランク定数hとの結びつきを表す式．たとえば，M. Planck(プランク)は振動数νの荷電振動子のとりうる力学的エネルギーを

ε ＝ nhν　(n ＝ 0，1，2，…)

とし，N. Bohr(ボーア)は水素原子内電子の角運動量のとりうる値は

2π p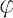 ＝ nh　(n ＝ 1，2，3，…)

で定まると考えた．これらが量子条件である．このように，いろいろな問題のなかでいろいろな量に与えられる量子条件にある統一的表現を与えることはA.J.W. Sommerfeld(1913年)によってなされた．かれの表現では，f個の自由度をもつ系の量子条件は一般化座標 q_i および共役な一般化運動量 p_i により，作用積分，

∫ p_idq_i ＝ nh　(n ＝ 1，2，3，…；i ＝ 1，2，…，f )

で与えられる．これをとくにゾンマーフェルトの量子条件という．周期運動のときは q_i に関する積分はその1サイクルにつき行うものとする．等速円運動のときは

r ＝ 一定，p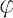 ＝ 一定
で上の表現がただちにボーアの量子条件を与える．次に，質量mの粒子が振動数ν，変位が

x ＝ a sin(2πνt)

の振動をしているとする．このとき，

速度 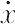＝ a(2πν)cos(2πνt)

運動量m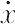 ＝ ma(2πν)cos(2πνt)

である．したがって，ゾンマーフェルトの量子条件は，

　　∫m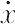dx ＝ ma² (2πν)² ∫ cos²(2πνt)dt

　　　　　　 ＝ ma²(2πν)∫₀^2π cos²ydy

　　　　　　 ＝ ma²(2πν)π ＝ nh

である．一方，この系の力学的エネルギーはx ＝ 0における運動のエネルギーに等しいから，

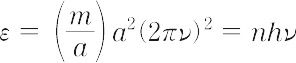
となる．これはPlanckが最初振動子エネルギーに与えた量子条件に等しい．このように，量子条件において，ある物理量の量子性を表しておくと，それらの量を含んだ系のエネルギーが連続でなくとびとびの値になる．Sommerfeldはこのような理論を原子のエネルギー準位について展開した．

出典　森北出版「化学辞典（第2版）」

日本大百科全書(ニッポニカ)

量子条件
りょうしじょうけん
quantum condition

古典論に基づいた力学系の取扱いから量子力学による取扱いに移っていく場合の条件。

　量子力学の発見以前にも量子を導入して力学系に対するさまざまな試みが行われた。古典論に基づいた水素原子内電子の軌道には連続的に変化する無数のものがあるが、ボーアは、このなかから実際に定常状態の電子の軌道を決定する条件として、軌道に対して求めた作用（運動量pを座標qで運動の一周期に対して積分した量）をプランク定数hの整数倍に等しくするという条件を課した。すなわち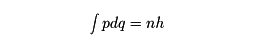

であり、量子条件の狭義としてこのボーアの量子条件をさすこともある。

　量子力学においては座標と運動量がqp-pq=iħ（ħはプランク定数hを2πで割ったもの）という条件を満たさねばならない。この条件は、二組の物理量q、pの積の順をかえたときの差すなわち交換関数を与えているものであって、古典論に基づいて座標qと運動量pにより記述されている力学系を量子力学的に扱う場合に必要な条件である。一般に二つの特別な物理量の組み、すなわち正準共役(きょうやく)は、物理量に交換関係を用いた条件を課することによって、量子力学的な取扱いが可能になる。この場合、量子条件は交換関係によって与えられている。ハイゼンベルクはボーアの量子条件から交換関係の形の量子条件をみいだし、量子力学の確立に導いた。

［田中　一］

[参照項目] | ハイゼンベルク | プランク定数 | ボーア | 量子力学

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

量子条件
りょうしじょうけん
quantum condition

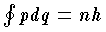ボーアの原子理論における根本的な仮定の1つ。水素原子の中の電子は原子核を中心とする円運動をしているとすると，古典力学では，軌道の半径はゼロから無限大までのどの値もとることができる。しかし N.ボーアはこの無限の軌道のうち，角運動量が h/2π ( h はプランク定数 ) の整数倍になる軌道だけが実現されると考えた。座標 q とそれに共役な運動量 p を用いて書くと，この条件は作用量 となる。これをボーアの量子条件という。 n は 1，2，3，… というようにとびとびの値しかとれず，量子数と呼ばれる。量子条件によると，円運動の半径もとびとびの値しかとれず，量子数 n が大きくなるほど，円の半径は大きくなる。最小の半径は 5.3×10^-11m で，水素原子のボーア半径と呼ばれる。量子力学では，座標と運動量を演算子と考えて交換関係をつくると，同じ結果が得られるから，交換関係を量子条件ということもある。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

量子条件【りょうしじょうけん】

連続的な値をとる古典的な量を，とびとびの値をとる量子論的な量へおきかえる操作を量子化といい，その際量に課せられる条件を量子条件という。前期量子論のボーアの理論（1913年）では，〈原子核のまわりを円運動する電子の運動量と円周の長さとの積が作用量子（プランク定数）の整数倍に等しい〉という量子条件により，古典的には無数に可能な電子の運動状態から特定の定常な運動状態を選び出す。さらに，電子がエネルギーE₁の定常状態からE₂の定常状態に移るとき，E₁＞E₂ならエネルギーの放出（誘導放出），逆なら吸収が起こり，その振動数νはν＝（E₁−E₂）/hで与えられる。これを振動数条件という。→量子／量子論
→関連項目ゼーマン効果

出典　株式会社平凡社

改訂新版　世界大百科事典

量子条件 (りょうしじょうけん)
quantum condition

古典力学から量子力学への過渡期の理論であった古典量子論においては，運動は古典力学の運動方程式に従うが，その解のすべてが現実に実現されるのではなく，ある条件にかなうもののみが実現されるとした。その条件を量子条件という。N.ボーアは，原子核のまわりをまわる電子について〈角運動量はプランク定数hの整数倍になる〉を量子条件として原子構造論をたて，原子の線スペクトルを導きだした（1913）。量子条件には種々の形が提案され，日本の石原純の案（1915）もあったが，もっとも成功したのは作用量積分をhの整数倍とするA.ゾンマーフェルトのもので（1915），これは量子力学においてもWKB近似の範囲で成り立つ。
→量子力学
執筆者：江沢 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の量子条件の言及

【量子力学】より

…(2)電子はエネルギーE_nの定常状態から，より低いE_n′のそれに遷移することがあり，そのとき，で決まる振動数νの光を放出する。(3)電子の運動はニュートンの運動方程式に従うが，しかし初期条件に応じて運動はさまざまになるという古典力学の特徴は失われ，量子条件をみたす運動だけが定常状態として実現する。　ボーアは，電子が核を中心として円運動するものとして，運動方程式から単位時間当りの公転数νとエネルギーEの間に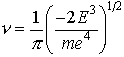，の関係があることを導き，定常状態のE＝E_n,ν＝ν_nは量子条件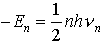，で選ばれるものとして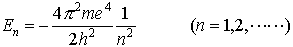，を得た。…

※「量子条件」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」