精選版 日本国語大辞典 「ユークリッド幾何学」の意味・読み・例文・類語
ユークリッド‐きかがく【ユークリッド幾何学】
日本大百科全書(ニッポニカ) 「ユークリッド幾何学」の意味・わかりやすい解説
ユークリッド幾何学
ゆーくりっどきかがく
Euclid geometry
ユークリッドがその著『原論』(『ストイケイア』Stoikheia)で展開した幾何学。『原論』はその時代までのギリシア数学を集大成した13巻の書で、平面幾何(第1巻~第6巻)、整数論、実数論(第7巻~第10巻)、立体幾何(第11巻~第13巻)からなる。整数、実数に関する部分も幾何学の用語を使っているうえに、『原論』の大部分が幾何学なので『幾何学原論』ともよばれる。『原論』で扱われている幾何学は現在n次元まで拡張されているが、19世紀以後続々と出現した他の幾何学と区別して、これをユークリッド幾何学といい、『原論』におけるように論証を主体とする方法によって行う二、三次元のユークリッド幾何学をとくに初等幾何学とよぶ。『原論』は23個の定義、5個の公準、5個の公理から始まる。定義によって用語の説明をしたのち、次の5個の公準(今日のことばでは幾何学の公理)をあげている。
(1)2点を線分で結ぶことができる。
(2)線分は直線にいくらでも延長できる。
(3)任意の点を中心とした任意の半径の円を描くことができる。
(4)直角はすべて互いに相等しい。
(4)二つの直線l、l′が他の直線l″と交わってできる交角α、βがα+β<180゜を満たすならば、lとl′とは交角α、βのある側に延長するとかならず交わる。
5個の公理は「全体は部分より大きい」「同じものに等しいものはまた互いに等しい」のように数学一般について成り立つ命題を述べている。ユークリッドは、幾何学のそれまで知られている数多くの定理を、どの定理もそれ以前の定理と論証だけから証明するという論証体系にまとめ上げ、この体系の大前提として先に述べた5個の公準を採用した。土地測量術や天体観測術への応用から出発した幾何学はこの『原論』によって初めて壮大な論理的体系をもつ学問に発展することとなった。
第五公準は他の5個の公準ほど簡明でなく、また不自然な感じがあるために、他の公準から証明できるのではないかという疑いがもたれた。この公準は、その後「1直線外の1点を通ってちょうど1本の平行線が存在する」(平行線公理)と同値であることがわかったが、他の公準から証明されるに違いない(と信じられる)命題を公準として残しておくことは、完璧(かんぺき)な論証体系としての幾何学にとって大きな汚点と考えられた。そのため平行線公理の証明に多くの優れた学者が立ち向かったが、時間と労力を飲み尽くす泥沼であった。『原論』から2000年もたった1830年前後になって、ロシアのロバチェフスキーとハンガリーのボヤイは独立に、第五公準を「1直線外の1点を通って2本の平行線が存在する」という別の公準で置き換えても矛盾のない幾何学が建設されることを示した。これがのちに双曲幾何学とよばれる非ユークリッド幾何学である。この発見はユークリッド幾何学の唯一性を否定し、幾何学の新時代の幕開きとなったものである。実際、リーマン、クラインなどの研究によって新しい、より一般的な幾何学が続々誕生していった。
一方、16世紀におけるデカルト、フェルマーによる座標系の考案は、ユークリッド幾何学に計算を利用して研究する道を開いた。のちに解析幾何学とよばれるこの方法は、ユークリッド幾何学の内容をさらに豊かにし、かつ三次元から一般のn次元への拡張を可能にした。すなわち、n次元数空間の2点(x1,x2,……,xn),(y1,y2,……,yn)の間の距離を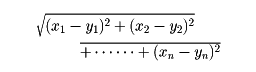
と約束したとき、この空間をn次元ユークリッド空間といい、合同変換(長さを変えない1対1点対応)によって不変な図形の性質を研究する学問がn次元ユークリッド幾何学である。幾何学はユークリッド幾何学以外にもたくさんあるが、『原論』における論証の進め方は現在でも模範とすべきものであり、ユークリッド幾何学は他の諸幾何学の基礎である。また、抽象数学の多くはユークリッド幾何学で成り立つ図形の諸性質を抽象化することから出発している、という意味で、ユークリッド幾何学は現代数学の土壌ともいうことができる。実用面でも、宇宙規模の測量はともかく、地上の小範囲においては依然としてユークリッド幾何学が使われていることには変わりはない。
[立花俊一]
『ユークリッド著、中村幸四郎他訳『ユークリッド原論』(1972・共立出版)』
改訂新版 世界大百科事典 「ユークリッド幾何学」の意味・わかりやすい解説
ユークリッド幾何学 (ユークリッドきかがく)
Euclidean geometry
古代エジプトにおいて測量の技術より得られた図形に関する経験的知識はギリシアにもたらされて,論理的に整理されて体系化され,幾何学となった。ユークリッド(前300ころ)はこれを集大成して《ストイケイア(原論)》全13巻を編んだ。ユークリッド幾何学とは本質的にこの著作に述べられている幾何学のことである。これは中学校や高校で学習する図形に関する性質をおもな内容としていて,初等幾何学とも呼ばれている。《ストイケイア》は若干の命題を公理として仮定し,これらより論理的に正しい推論だけによって得られる命題を定理とする。これらの公理のなかに,第5公準と呼ばれる次のものがある。〈一つの直線が二つの直線と交わり,その一方の側にできる二つの角を合わせて2直角より小さくなるときは,それらの二つの直線をどこまでも延長すれば,合わせて2直角より小さい角の側で交わる〉(図)。これは重要な公理で,〈三角形の内角の和は2直角である〉という命題や,平行線の公理と呼ばれる〈直線外の1点を通ってこの直線に平行な直線はただ一つに限る〉という命題と同値であり,三平方の定理もこの公理なしでは証明できない。ところで第5公準は,その陳述,内容よりして,公理よりはむしろ定理のように感じられるので,この公準は後世にいろいろの批判をうみ,長い間の苦闘の末,19世紀前半にはこの公準を否定する幾何学が生まれた。すなわち,〈平面上で,直線外の1点を通ってこの直線に交わらない直線は無数にある〉と仮定してもなお矛盾のない幾何学がりっぱに組み立てられることがN.I.ロバチェフスキー,ボーヤイJ.によって発見された。ユークリッド幾何学は,非ユークリッド幾何学と呼ばれるこの新幾何学に対することばとして,それは平行線公理をみたす幾何学という意味をもつ。19世紀後半になると,射影幾何学をはじめいろいろの幾何学が発見され,幾何学とは何かということが問題となった。F.クラインは有名なエルランゲン・プログラムでこれに答えて,〈一つの空間Sとその上の一つの変換群Gを与えたとき,Sの図形の性質のうちGのすべての変換で不変なものを研究することにより一つの幾何学が定まる〉とした。この考えを採るとき,ユークリッド幾何学は三次元空間R3とその上の合同変換群(広義には相似変換群)によって定まる幾何学であるといえる。19世紀後半には,また,《ストイケイア》も細かく検討すると完全無欠な論理体系といえないことが気づかれ,ついにD.ヒルベルトの《幾何学基礎論》(1899)において《ストイケイア》の完ぺきな再構成がなされた。そこでは点,直線,平面に関し,結合公理,順序公理,合同公理,平行線公理,連続性公理と呼ばれる5群の公理が設定されている。これによりユークリッド幾何学とはこれらの公理系から導き出される論理体系であると規定できることとなった。現今ではユークリッド幾何学は,平面R2や三次元空間R3に限らず,n次元ユークリッド空間Rnにおいて展開されている。
→幾何学
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「ユークリッド幾何学」の意味・わかりやすい解説
ユークリッド幾何学【ユークリッドきかがく】
→関連項目幾何学|射影幾何学
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「ユークリッド幾何学」の意味・わかりやすい解説
ユークリッド幾何学
ユークリッドきかがく
Euclidean geometry
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内のユークリッド幾何学の言及
【数学】より
…上の仮定のもとでは三角形の内角の和は2直角より小さくなるが,球面幾何学と多くの類似点をもつ幾何学が構成されることが示されたのである。このように平行線の公理を否定した命題を仮定した幾何学を非ユークリッド幾何学といい,それに対して《ストイケイア》に見られるような幾何学をユークリッド幾何学という。ガウス自身大きな三角形について実測し,その内角の和と2直角との差を調べたが,それは誤差の範囲内にあって,現象空間でどちらの幾何学が成り立つかについての結論は得られなかった。…
※「ユークリッド幾何学」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...