乱流（読み）ランリュウ（その他表記）turbulent flow

デジタル大辞泉

らん‐りゅう〔‐リウ〕【乱流】

流体の各部分が不規則に混合しながら流れる流れ。大気や河川の流れが障害物に当たって生じる流れの多くはこれである。→層流

出典　小学館

精選版 日本国語大辞典

らん‐りゅう‥リウ【乱流】

1. 〘 名詞 〙
2. ① 激しく乱れて流れること。また、その流れ。
   1. [初出の実例]「洲及島嶼位置の便宜に従ひ、之を一方の岸に結んで、乱流を防ぐ事」(出典：地方官会議日誌‐九・明治八年（1875）七月二日)
3. ② 各部分が不規則に混合しながら流れること。また、その流れ。
   1. [初出の実例]「白い靄の柱がひとすじすうっと立って〈略〉蚕糸の乱流のような先端を高空の澄んだ青の中へ徐々に融かしている」(出典：雪の下の蟹（1969）〈古井由吉〉)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

乱流 (らんりゅう)
turbulent flow

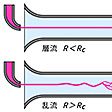
川の浅瀬におかれた小石の背後には，泡を含んだ美しい流れ模様がしばしば観察される。泡の挙動により，小石のまわりの流れは時々刻々不規則に変動する非常に複雑なものであることがわかる。このように規則性の乏しい流れを一般に乱流と呼ぶ。乱流に対比して，いわゆる流線形物体のまわりに実現される規則性の強い流れを層流laminar flowという。しかし，このような流れの分類は必ずしも確固たるものではなく，自然現象や各種の工学的機器内外で見られる流れにおいては，その不規則性の程度に大きな差異がある。そのため，ある流れを乱流的とみるかあるいは層流的とみるかは，そのような見方が流れの理解に好都合であるかどうかとも深く関係している。川の小石のまわりの流れでは，泡の存在によって乱れをみることができるが，われわれの日常生活では必ずしも乱れを直接みることができない。しかし，それらは程度の差こそあれ，ほとんど乱流といえる。

乱流はなぜ起こるか

層流から乱流への移り変りを見るために，管を流れる水の運動を考えてみよう。断面が円形の適当な長さの管の一端を貯水槽に連結し，圧力差を利用して他端から放水する（各家庭における水道の蛇口とそれにつけたホースを連想すればよい）。圧力差を小さくして水をゆっくり流す。このとき，貯水槽に近い管内の1点，例えば中心軸上の1点で色素を連続的に注入すると，色素は1本の直線的筋となって下流に流れていく。さらに，もう1点で色素を注入すると，これら2本の筋は互いに交わることなく流れていく。このように流体どうしが互いに層をなし，交差することなく流れる状態が層流である。次に，圧力差を上げ，水流を強くする。貯水槽に近い点で注入された色素は，下流に流されるに従ってその筋は波打ち始め，筋自体太くなり，ついには管壁まで色素が広がってしまう。このような状態が乱流である。

　管内での乱流の発生を最初に組織的に研究したのが，O.レーノルズである。彼はこの研究において，流量の目安となる中心軸上流速U，円管の半径a，流体のねばさを表す動粘性係数νの三つから作られる単位をもたない量，すなわち無次元量Ua/νの大きさが，乱流状態が出現するか否かを決定することを発見した。この無次元量は通常レーノルズ数と呼ばれ，R_eの記号を用いて表される。レーノルズの実験では，R_eが1000程度以上になると層流状態が維持できないことが示された。他の流れにおいても，流れの中の代表的速度U，代表的長さL，動粘性係数νを用いて作られるレーノルズ数UL/νが1000程度を超えると，流れは乱流状態へ移行し始めることがその後の多くの研究でわかっている。

　1000程度のレーノルズ数がどの程度のものであるかを見るために，二，三の具体例をあげる。各家庭での水道管においては，U≅100cm/s（管の平均速度），L≅1cm（管の半径），ν≅0.01cm²/s（常温での水の動粘性係数）であるので，R_e≅10000となる。人が歩くときは，U≅100cm/s（歩行速度），L≅30cm（肩幅の半分），ν≅0.1cm²/s（常温での空気の動粘性係数）であり，R_e≅30000となる。このような例から，われわれを取りまく流体運動の大部分は乱流と関連していることが理解される。レーノルズ数が大きくなればなるほど，一般には不規則性が強くなるので，ある流れを乱流とみなしたほうが理解しやすいかどうかは，レーノルズ数の大小による。

　次に，乱流がなぜ発生するかを考える。レーノルズの実験では，レーノルズ数が1000程度以上で乱流の発生がみられた。しかし，貯水槽と管の連結部分をなめらかにすればするほど，乱流の発生するレーノルズ数（臨界レーノルズ数）は上昇する。このことより，臨界レーノルズ数以上では管の入口などで流体に加えられたかく乱が発達して乱流となると同時に，臨界レーノルズ数も加えられるかく乱の大きさによることがわかる。結局，乱流の発生は基本となる層流状態（上の例では貯水槽近くの流れ）の安定性と密接に関係している。

乱流と日常生活

日常生活で関連する流れの大部分は乱流的であるが，この事実がわれわれの生活にどのような影響を与えるかをみてみよう。川の小石の背後の流れ模様から，乱流は非常に細かい流体運動を含んでいることがわかる。この細かい運動は通常渦と呼ばれるが，渦どうしは互いにぶつかり合い，その間に摩擦が生ずる。流体運動のエネルギー損失は摩擦に起因する熱エネルギーへの変換であるため，小さな渦が多ければ多いほど流体間の接触面が増え，エネルギー損失が大きくなる。このエネルギー損失という観点からみると，乱流の発生ははなはだ好ましくない現象といえる。航空機，新幹線に代表される高速列車，自動車などで乱流の出現を抑える形状すなわち流線形が考慮されているのはまさにこのためである。

　しかし，乱流現象はエネルギー損失という面でのみわれわれの日常生活と結びついているのではない。卑近な例として，コーヒーに砂糖を溶かすことを考える。コーヒーを満たしたカップに砂糖を静かに入れただけでは，砂糖の広がり（拡散）は水の分子運動による分子拡散が主であり，非常に遅い（水を満たしたカップにインキを落とした場合と状況は同じである）。スプーンをカップ中で適当な速さで円状に動かすと，当然砂糖の拡散は速くなる。次に，同じ程度の速さでスプーンを不規則に動かしてみる（速く溶かそうとするとき，われわれは日常無意識のうちにこれをしている）。このほうが砂糖の拡散はずっと速いが，その原因はカップ中に乱れが生じ，乱れに乗って砂糖が四方八方へ広がるためである。乱流によるこのような拡散は乱流拡散と呼ばれ，ほとんどの場合分子拡散に比べてはるかに大きい。汚染物質の大気および海洋，河川での拡散など乱流拡散現象は，われわれの日常生活と多大の関連をもっている。

乱流の研究

流速が音の速さよりずっと小さいときは，流体密度の変化を考える必要はない。このとき，流体運動およびその中での熱や物質の拡散を支配する方程式は，三次元形で，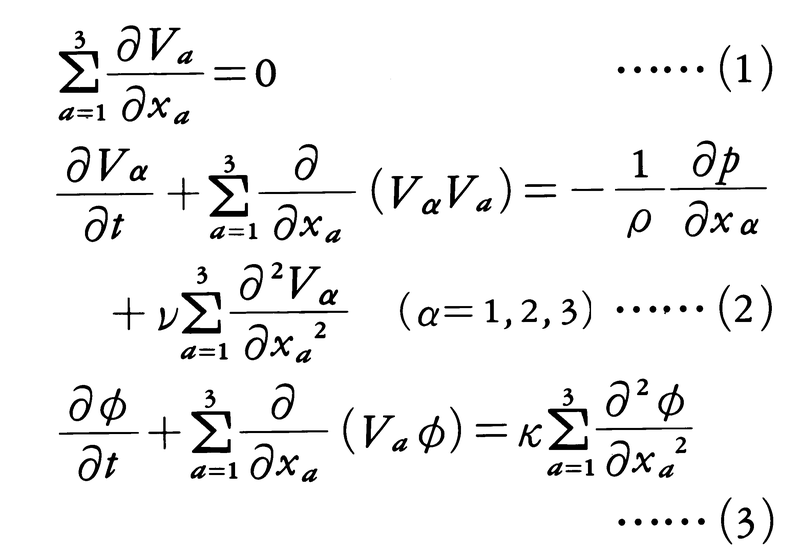

と表される。ここで，tは時間，x（＝x_a;a＝1，2，3）は三次元の空間座標，V（＝V_a;a＝1，2，3）は流速べクトル，pは圧力，ρは流体密度，νは動粘性係数，φは温度または物質濃度，κはφの拡散係数である。（1）は流体の非圧縮性を表す連続の方程式，（2）は非圧縮性流体の運動を記述するナビエ=ストークス方程式，（3）は流体中でのφの拡散を支配する拡散方程式（熱のときは，一般に熱伝導方程式と呼ばれる）である。

　乱流運動を平均部分とそれからのずれ（じょう乱部分）に分け，

　V＝U＋u，U＝〈V〉

　p＝P＋p′，P＝〈p〉

　φ＝Θ＋θ，Θ＝〈φ〉

と書く。ここで，〈f〉は量fの平均を意味し，ある乱流現象を多数回繰り返し，その平均を取るというアンサンブル平均を用いる。その結果，平均部分U，P，Θに対する方程式は，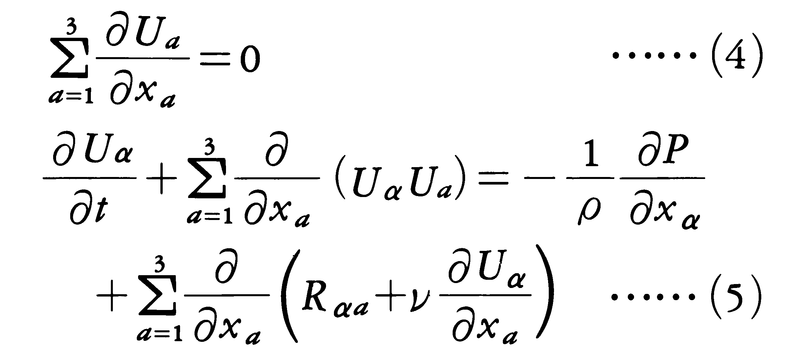



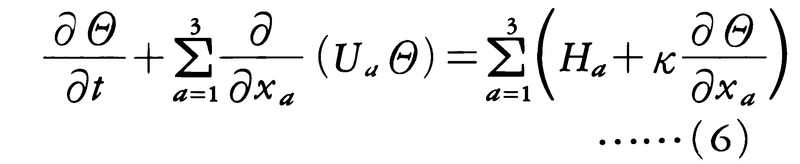
と表される。ただし，上の式で，R_αβ＝－〈u_αu_β〉，H＝－〈uθ〉である（β＝1，2，3）。（5），（6）をもとの方程式（2），（3）と比べると，唯一の差異はR_αβ，Hの出現である。R_αβ，Hはそれぞれレーノルズ応力，スカラー輸送量と呼ばれている。これらは，平均操作によって乱流場を粗視化したとき，すなわち時間・空間的変動がゆっくりした平均部分のみに注目したとき現れる唯一の乱れの影響である。例えば，uθは，θが単位時間に単位質量当りの乱れた流体によって運ばれる量であることから，Hはスカラー量の乱流拡散を表している。乱流中では，分子拡散に比べて乱流拡散がはるかに大きいことを述べたが，このことは｜H｜≫κ｜gradΘ｜を意味する。他方，u_αu_βは乱れによって運ばれる運動量輸送であることから，R_αβは応力という物理的意味をもつ。一般に｜R_αβ｜≫ν｜∂U_α/∂x_β｜が成り立ち，乱流中でのエネルギー損失の増大はこの事実と密接に関係している。（4）から（6）はR_αβ，Hの出現により，これらをU，Θと何らかの関係で結びつけない限り，閉じた方程式系とはならない。

　乱流の非実験的研究は二つに大別される。一つは，すでに豊富に得られている実験的成果に基づいて，次元解析，テンソル解析などを駆使してR_αβ，H，U，Θの間にモデル関係式（あるいはモデル方程式）を構成する乱流モデルと呼ばれる方法である。もう一つは，渦の運動を多体効果的にとらえ，これを理論的に解析し，上述の関係式を見いだそうとする統計力学的方法である。いずれの方法においても，未解決の問題が山積しており，実験的方法が乱流の研究においては先行しているというのが現状である。
執筆者：吉沢 徴

海洋乱流

海水のランダムな運動を海洋乱流という。海洋乱流は通常の乱流がもつ特性に加えて次のような特徴をもっている。

　（1）平均場の強さに比べて乱れが非常に小さいとはいえない。したがって乱れと平均流を識別するのが難しい。（2）海洋乱流は一般に非等方性が著しい。これは密度成層の影響で鉛直方向の乱れがおさえられるためである。つまり水平方向の乱れが鉛直方向に比べて非常に大きい。ただし乱れの規模が1m以下の小さい乱流に関しては等方的とみなせることも多い。（3）乱流が非定常的である。すなわち乱れの統計的性質が時間的に変動している。（4）海洋乱流は空間的にも一様ではない。とくに鉛直方向の変化が大きく，たとえば，海の上層の混合層における乱流とその下の温度躍層の乱流では性質が異なる。（5）外力として入るエネルギーは最も規模の大きい乱れに与えられるだけでなく，他の規模の乱れにも直接与えられていると思われる。たとえば風は風波固有の規模の乱れに，また起潮力は潮流の規模の乱れに，それぞれ直接エネルギーを供給していると考えられる。

　海洋中の乱流の観測から，そのエネルギー密度を計算するとスペクトルにいくつかのピークが見られ，乱れのエネルギーが集中している周期が現れる。とくに半日周潮周期（12.42時間）と慣性振動周期（この場合は18.9時間）ではその集中度が高い。また半日周潮より短い周期の乱れのエネルギースペクトルは，振動数が大きくなるに従って比較的規則的に減り，その減り方は理論値の－5/3乗則にほぼ合っているといえる。

　なお，大気における乱流現象は一般に乱気流といい，これについては〈乱気流〉の項を参照されたい。
執筆者：宮田 元靖

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

乱流
らんりゅう
turbulent flow

川の流れを見ると、岩や橋脚などの障害物の上流側では流れは滑らかであるのに、下流側では大小さまざまの渦巻が現れ、流れはきわめて不規則、複雑である。また、水道の栓をすこしひねると、水は透明な細い棒になって落下するが、栓をいっぱいにあけて大量に流すと、水の棒は白く泡立つようになる。このように不規則で乱雑な流れを乱流、これに対して滑らかな流線をもつ流れを層流という。

［今井　功］

レイノルズの実験

流れの状態に層流と乱流の違いがあることに注目して初めて実験的な研究を行ったのはイギリスのO・レイノルズで、1883年のことであった。彼は、円管を通る水の流れが、流速の小さいときは層流、流速が大きくなると乱流になることをみいだした。実験結果は定量的に次のように表される。管の直径をd、流体の密度をρ、粘性率をμ、平均流速（流量÷断面積）をūとするときR=ρūd/μは無次元の数でレイノルズ数とよばれる。このRがある値R_cより小さいときは層流、大きいときは乱流となるのである。R_cを臨界レイノルズ数という。この場合R_cは約2000である。管を通る流れとは限らず、物体表面を覆う境界層についても、その厚さδ、境界層のすぐ外側の流速uを基準にしてレイノルズ数Rδ=ρuδ/μをつくると、これに対しても臨界レイノルズ数が存在し、それ以下では境界層の流れは層流、以上では乱流になる。

［今井　功］

乱流の渦

乱流は時間的にも空間的にも不規則に変動する流れで、大小さまざまな渦から構成されていると考えられる。この渦の乱雑な運動は気体分子の熱運動になぞらえられる。たとえば、流れの中の流速や温度の分布が一様でない場合には、一般に流体の粘性や熱伝導性によって不均一はならされて一様分布に近づく。気体では、粘性や熱伝導性は気体分子の熱運動によって、運動量や運動エネルギーが運搬されることに起因するのであるが、これに対して乱流では、これを構成する渦によって、分子運動よりもはるかに大規模に均一化作用が行われる。これは見かけ上、粘性や熱伝導性が大きくなることを意味する。水や空気中の汚染物質の拡散についても同様である。このため、乱流粘性（渦(うず)粘性）、乱流拡散係数（渦拡散係数）などの用語も使われる。

　いまx軸方向に速度uの流れがあるとする。平均的には流速が一定でUであるとしても、細かくみればu=U+u′であって、u′(x,t)は、場所xと時間tの関数として複雑に変化する。このu′によって乱れあるいは乱流が表される。u′の振幅の大きい場合、乱れは強く、u′の空間的・時間的変化の周期の小さい場合、乱れの寸法は小さい。すなわち乱流を特徴づける量として強さと寸法がある。乱流を構成する大小さまざまな渦の運動エネルギーの平均値が強さを表し、渦の大きさの平均値が寸法を表すのである。一般に、レイノルズ数の大きい流れはすべて乱流状態にあるということができる。

［今井　功］

大気中の乱流

地表面付近の風は、風速や風向が絶えず不規則に変化している。これを「風の息」という。風の息は、風が乱流であるために生じる。地表面には樹木や建造物などがあり、それに風が当たると、大小さまざまな渦が発生して風が乱流になる。また、地表面が滑らかであっても、地表面の摩擦によって風が弱くなり、強い風と弱い風が混じり合って渦が発生し、風が乱流になる。煙突の煙が上下に蛇行しながらたなびくのは、煙が風の中にある渦に巻き込まれるために生じる現象である。地表面から高度約1キロメートルまでの大気層は、とくに乱れの程度が大きく、自動車の排気ガスや工場から排出された煙を速やかに拡散させる作用がある。

　飛行機に乗って、高度5キロメートルから10キロメートルの上空を飛行していると、ときどきがたがたと揺れることがある。これは、上空の大気が乱流になっていることを示している。上空の乱流は、ジェット気流の近くや、下方に山があるときに生じることが多い。積乱雲の内部は激しい乱流である。晴天時に生じる上空の乱流を晴天乱気流といい、CAT（clear air turbulenceの略）ともいう。

　新聞の天気図を見ると、高気圧（時計回りの渦巻）や低気圧（反時計回りの渦巻）が描かれていて、形を変えながら西から東に移動している。このような地球規模の大気の流れも乱流と考えられている。変化の仕方が不規則なので、遠い将来まで天気の変化を予測することができない。天気予報のために毎日気象観測を行うのは、そのためである。

［木村龍治］

海洋の乱流

海水温は深くなるほど低くなるが、海面から10メートル程度は、深さによって水温は変化しない。そこを表層混合層という。水面に吹く風の作用で表層の海水がかき混ぜられるために生じる現象で、その内部は乱流である。場合によっては、水面に渦が無数に見えることがある。冬季に海面が冷たい空気に接触して冷やされる場合にも混合層が発達する。四国と淡路島の間の鳴門(なると)海峡のように潮流の強い海域では、地形の作用で渦が発生し、激しい乱流が生じる。100メートル以深の海底付近の流れは穏やかであるが、まれに、海底斜面に沿って土砂崩れのような現象が生じ、その際に、泥と海水が混ざり合った雪崩(なだれ)のような激しい乱流が生じる。これを混濁流（乱泥流）という。

　日本の黒潮や北アメリカのガルフストリーム（湾流）のように、強い海流が沖に向かう海域では、海流の蛇行によって渦が発生し、天気図に示される大気中の乱流のような大規模な乱流が生じている。

［木村龍治］

『A・H・シャピロ著、今井功訳『流れの科学』（1977・河出書房新社）』▽『木村龍治著『改訂版　流れの科学』（1985・東海大学出版会）』▽『流れの可視化学会編『流れのファンタジー――写真がとらえた流体の世界』（1986・講談社）』▽『H・テネクス、J・L・ラムリー著、藤原仁志・荒川忠一訳『乱流入門』（1998・東海大学出版会）』▽『木田重雄・柳瀬真一郎著『乱流力学』（1999・朝倉書店）』

[参照項目] | 渦 | ガルフストリーム | 境界層 | 混濁流 | 晴天乱気流 | 層流 | 流れ | レイノルズ | レイノルズ数

レイノルズの実験

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

乱流【らんりゅう】

各点における速度が大きさも方向も時間とともにきわめて不規則に変動する流体の流れ。層流に対する語。たとえば円管内の流れでは，レーノルズ数が約1000を超えると，層流が乱流に変わり（管内に色素を流して観察できる），ハーゲン=ポアズイユの法則が成り立たなくなる。乱流中では運動量やエネルギーの輸送が激しいため，粘性率，熱伝導率，拡散係数などの値は見かけ上非常に大きくなる。また流れが物体に及ぼす抵抗は，乱流の存在によって大きな影響を受けるので，航空などの実際問題で重要である。→流体力学
→関連項目渦｜流線型

出典　株式会社平凡社

普及版 字通

【乱流】らんりゆう（りう）

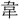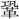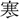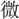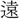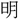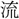放縦。渡江。氾濫。激流。唐・応物〔洛より舟行して黄河に入る、即事～〕詩　樹、依(いび)たり、天の外　夕陽滅す、亂の中

字通「乱」の項目を見る。

出典　平凡社「普及版 字通」

化学辞典 第2版

乱流
ランリュウ
turbulent flow

流体が平均流速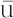で流れているとき，レイノルズ数がある一定値(臨界レイノルズ数)以下であれば，流体中のある点での流れの方向，速度の大きさは一定に保たれ，乱れのまったくない層状の流れ(層流)となる．なんらかの原因で流体中に乱れが発生しても，この乱れは層流の場合，流体の粘性のために減衰して消滅する．流体の流れが速くなり，レイノルズ数が臨界レイノルズ数以上になると，流体中に生じた乱れはもはや減衰せず，逆に慣性力が粘性力を上まわるために増幅され，この乱れによりある点での流れの方向，速度の大きさは絶えず不規則に変化する(乱流)．この乱れによる混合のために，管内を流れる流体の速度分布は層流の場合よりもはるかに一様に近づく．乱流では壁近くの速度勾配が増すので摩擦抵抗が大きくなる．したがって，圧力損失も大きく，平均速度の約2乗に，また流体密度に比例するようになり，流体の粘度の影響は減少し，管壁の粗滑の影響が現れてくる．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

乱流
らんりゅう
turbulent flow

流体の速度や圧力などが不規則に変動する流れをいう。また，このような不規則な変動を乱れという。これに対して，乱れを含まない流れを層流という。流れのレイノルズ数が低い場合には，粘性の減衰作用が大きいため，流れは安定で，層流状態に保たれるが，レイノルズ数がある臨界値以上に大きくなると，流れは不安定になり，乱流状態に移行しやすくなる。層流から乱流への遷移過程では，撹乱の線形成長に続いて非線形成長が起り，完全な乱流へと推移することが知られている。乱流の特徴はさまざまなスケールの渦運動と，それに伴う強い攪拌効果および小さなスケールの渦の粘性によるエネルギー散逸にある。

出典　ブリタニカ国際大百科事典 小項目事典

栄養・生化学辞典

乱流

　層流に対する語．不規則に変動する流れ．

出典　朝倉書店

世界大百科事典（旧版）内の乱流の言及

【渦】より

…しかし実際には，粘性のきわめて小さい流体でも，物体面に角があったり，流速がある限度を超過したりすると，境界層が物体面からはがれて流れの中に渦が現れることになる。自由な渦層は一般に不安定であって大小の渦が複雑に乱れた渦運動(乱流)に移行する。
［渦線］
　流れのようすをわかりやすくするのに流線という概念が用いられるのと同じように，渦の運動には渦線というものが用いられる。…

【管】より

…しかし実際には，管壁との摩擦によって壁近くでは遅く，管の中央で最も速く流れる。その速度分布は，流れが層流か乱流かによって大きく変化する。平均流速，内径d，流体の密度ρ，流体の粘性率μから計算されるレーノルズ数Re＝ρd/μが小さい(約2300以下)ときは，管内の流れは層流となり，図-aに示すように放物線状の速度分布となる(最大速度は平均速度の2倍)。…

【乱気流】より

…大気の乱流をいう。乱流とは流体力学上の用語で，流体の各部分が平均流のまわりに不規則な運動をしながら流れる状態をいう。…

※「乱流」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」