境界層（読み）きょうかいそう（英語表記）boundary layer

精選版 日本国語大辞典

きょうかい‐そう キャウカイ‥【境界層】

〘名〙 空気や水など粘性の小さな流体と、その中に置かれた物体との間にできる粘性のきわめて大きな薄い層。この層の外側を近似的に完全流体とみなし、内側を粘性流体として考えたもの。航空力学の遷音速領域の重要問題となっている。

出典　精選版 日本国語大辞典

デジタル大辞泉

きょうかい‐そう〔キヤウカイ‐〕【境界層】

空気・水など粘性の小さい流体が物体の回りを流れるとき、物体の表面にできる粘性の大きくなった流体の薄い層。

出典　小学館

改訂新版　世界大百科事典

境界層 (きょうかいそう)
boundary layer

粘性が小さくて無視できるような流れ（主流）の中でも，物体面や壁面などの境界では粘性を無視することのできない薄い層が存在し，この層を境界層と呼ぶ。現実の流体では粘性があるため，流体と壁との境界では相対速度は0となる（粘着条件）。粘性を0とした理想化を行った完全流体として扱った場合，その理論は数学的にも簡潔なものとなるが，粘着条件を満足することができず，一般に壁に平行なすべり速度が現れる。また完全流体では，その中を一定速度で進行する物体に働く抵抗が0になるというダランベールのパラドックスを生ずる。境界層という考え方は，これらの矛盾を救済するためにL.プラントルによって1904年に導入されたもので，近代流体力学の基礎を作った。

境界層理論

いま無限に広い静止平板の外側の流体が，一定速度Uで壁に平行に動き始めたとしよう。実在の流体では粘性のために壁面での流体の速度は0となるから，壁の表面付近には，速度こう配があって渦が分布している領域が存在する（図1）。これが境界層と呼ばれるもので，その厚さは，壁面での速度のすべりが時間の経過とともにならされるため，しだいに厚くなっていくはずである。流体が動き始めてからの経過時間をt，νを動粘性率（粘性率μを密度ρで割ったもの）とすれば，境界層の厚さδは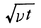に比例して増大する。この考えを定常な流れ（速度U）に平行におかれた半無限の平板に拡張し，前縁を原点として平板に沿った距離をlとすれば，平板に沿って流れが進む時間tはl/Uであるから，境界層の厚さδは平板に沿って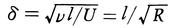（ただし，R＝Ul/ν）となり，lが大きくなるほど境界層は厚くなることがわかる（図2）。ここでRはレーノルズ数と呼ばれる無次元の量で，流れを支配する重要な量である。レーノルズ数が大きい流れ（νが小，Uが大）では，境界層の厚さδがlに比べて非常に小さいが，その中では速度こう配はU/δの程度に大きくなり，これに粘性率μを掛けた摩擦力はμが小さくてもかなりの値をとることができる。プラントルは以上の考えを一般にレーノルズ数の高い流れに押し進め，（1）物体の外部の流れについては完全流体の理論がそのまま成立するとし，壁面での圧力とすべり速度を見いだし，（2）境界層内では（1）の圧力をそのまま用い，壁面の曲率を無視するなど境界層の厚さが薄いことを利用した近似方程式（境界層方程式）を立て，（3）この方程式を，壁面の粘着条件を満足し，壁面から遠いところでは（1）のすべり速度に近づくという条件のもとに解けばよいことを提唱した。これはダランベールのパラドックスを救済するばかりでなく，主流としてそれまでの完全流体の理論の成果をそのまま採用できるという点で画期的なものであった。

境界層内の圧力と境界層の剝離

壁面の曲率があまり大きくなければ，境界層内の圧力は，壁に垂直な方向には一定であるが，平板に沿う定常な流れでないかぎり流れに沿っては変化する。下流にいくにつれて圧力が降下する例は，物体の前面や先細の管の中の流れなどに見られ，主流の速度は下流に向けて加速される。このときは境界層の厚さを与える式からもわかるように，境界層の厚さの下流に向けての増加は抑えられ，加速が大きい場合には（Uがlに比例して増大するときを境にして）むしろ薄くなっていく。これと反対に物体や突起の後方，あるいは先太の管では，下流のほうの圧力が高くて流れが減速され，境界層の厚さの増大が助長される。下流の圧力上昇は境界層に垂直な線上ではどこでも同じであるから，それが大きいと速度の遅い壁面近くで流れの向きが逆転して（逆流という），上流の流れともども向きを変えて主流中に向かい，主流中に渦を放出することになる。これを境界層の剝離という（図3）。また壁の上で剝離の始まる点を剝離点というが，そこでの摩擦抵抗は0となる。このようなことが起こると，下流では境界層の近似の基になった仮定が成り立たなくなり，一般に流れは不安定となり，複雑に時間的な変動をする乱流に移行することもあって主流は大幅な変更を受ける。整然とした流れ（層流）の乱流への移行は遷移と呼ばれ，レーノルズ数の高い境界層の宿命である。遷移は剝離以外にも主流の乱れ，境界の突起や粗さ，圧力上昇など多くの要因が引金となって引き起こされ，その過程もきわめて複雑である。
→乱流

乱流境界層

乱れた境界層は，乱れのない層流境界層に対比して乱流境界層と呼ばれる。乱流境界層は流れの激しい変動によって厚さが増す反面，平均速度が断面にわたって一様化されるので，壁面での速度こう配が大きく，摩擦抵抗の増大と渦の集中をきたす。また壁の近くの流速が層流境界層に比べて小さくならないために，下流の圧力が上昇する場合でも，剝離が妨げられるという効果を生む。剝離が起こると背後の圧力降下が起こってそのための抵抗増加や，着力点の急激な変化による翼の失速などの好ましくない結果につながるので，場合によっては遷移を速めたほうがよいことがある。このため境界層の遷移と剝離を適当に制御することは重要な問題であり，流線形の物体にしたり，飛行機のフラッグなどのように物体の形を変えたり，あるいは吹出しや吸込みをつけるなどいろいろなくふうが行われている。
→流線形

その他の境界層

回転流体の上下面や側面に出現するエクマン層やスチュアートソン層，電導性流体中で磁場に垂直な面に生ずるハルトマン層などは広い意味の境界層であって，前2者は慣性力の代りに回転流体に特有のコリオリの力，後者は電導性流体中での電流に働く力が粘性力とつり合ってできるものである。また振動流中の物体面にできる境界層をストークス層，平行な異速度流の間の渦層や噴流など物体のないところに生ずる境界層を自由境界層ということがある。このほか，境界層の概念を拡張して，熱伝導など散逸が小さな一般の場について，場の量の法線方向のこう配が大きく，散逸の担い手となるような薄層を境界層と呼ぶこともある。
執筆者：橋本 英典

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

境界層
きょうかいそう

すべての流体は粘性をもっている。水や空気の一様な流れの中に物体を置くと、流体は物体の表面に粘りつく。つまり物体表面で流速はゼロである。物体から離れるにしたがい、流れは一様流の速度になる。このような物体表面から一様流速になるまでの流速が急に変化する薄い層を境界層という。あるいは、静止した流体中で物体を動かすとき、物体に引きずられて動かされる物体表面付近の流体の層を境界層という。この境界層の厚みは粘性が大きいほど厚くなる。物体が水や空気中を動くとき受ける抵抗は、この境界層内の粘性によって引き起こされるもの（摩擦抵抗）である。円柱や球のような鈍い物体の場合、物体表面に働く圧力勾配(こうばい)のため、境界層内で逆流が発生し境界層が物体表面からはがれて、下流側へ押し出されていく。これを境界層のはがれといい、物体の後ろに渦の層ができることになる。この渦は、次々に分裂して複雑な乱流をつくる原因となる。このような場合、物体の上流側と下流側で流体から受ける圧力に差が生じ、摩擦抵抗以外に圧力抵抗も受けることになる。飛行機の翼のような流線形の物体では、境界層のはがれが生じにくく圧力抵抗がほとんど働かない。

［池内　了］

大気の運動と境界層

境界層は、層流境界層と乱流境界層に大別される。層流境界層は固体壁に隣接した流体の薄い層で、ここでは分子粘性による応力が支配的である。乱流境界層は層流境界層に隣接する乱流層で、ここでは乱渦による応力が支配的である。大気の運動も、地球表面近くでは地表面の影響を強く受け、地表面に接した薄い層では分子粘性による応力が支配的である。

　気象学では、特別の場合を除き、分子粘性による応力を無視することができるので、ここでは乱流境界層のみを考える。大気の運動が地表面の摩擦によって特有の力学的特性を表す気層を（大気）境界層とよんでいる。この層の厚さは地表から約1キロメートルである。これより高いところでは、地表の摩擦の影響がほとんどないので、これを自由大気とよぶ。自由大気では、地衡風の関係が近似的に成立するので、地表面から鉛直方向に風向を順次たどると、地衡風向と一致する高さに達する。この高さを摩擦高度とよぶ。これは大気境界層の高さを知る目安となる。大気境界層は下部と上部に大別される。下部境界層は地表から約100メートルの高さまでの気層をさし、地表境界層または接地（境界）層とよばれる。地表境界層と大気境界層を同義に用いることがある。この層内ではシャー応力が一定とみなされ、空気の運動は摩擦力のみに支配される。地表境界層のうち、対流によって空気が上下に混合される気層を（大気）混合層とよぶ。混合の及ぶ高さは、最高気温が出る日中にもっとも高くなる。混合層の厚さと層内の平均風速は大気汚染の予報に有力な目安を与える。上部境界層は地表境界層と自由大気の中間にあたるため、転移層またはエクマン（境界）層とよばれる。地表面から鉛直方向に風のベクトルの先端を順次連ねて得られるスパイラルを、エクマン・スパイラルとよぶ。この層内では、シャー応力が一定でなく、気圧傾度力、偏向力および摩擦力が近似的に平衡している。大気境界層内の風は摩擦力のために等圧線を横切って低圧部に向かう成分を有している。このため、地上の低気圧と高気圧にはそれぞれ水平収束と水平発散が対応し、大気中のエネルギー収支や、降水現象に関係の深い水蒸気の収支、また台風など擾乱(じょうらん)のエネルギー機構に対し重要な役割を演じている。

［股野宏志］

[参照項目] | 渦 | 地衡風 | 抵抗 | 流れ | 粘性 | 乱流

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

境界層
きょうかいそう
boundary layer

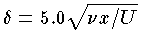粘性流体の流れにおいて，レイノルズ数が非常に大きいときには，物体表面に沿って，速度勾配，すなわち渦度がきわめて大きな薄い層ができる。これを境界層という。境界層の概念は 1904年に L.プラントルによって導入されたもので，これによって，完全流体の理論を中心とする数学的な流体力学が実際の現象と矛盾なく接合され，近代流体力学の基礎がつくられた。すなわち，境界層の内側では粘性を考慮した取扱いが必要だが，外側では完全流体の理論が成立する。物体表面から，速度が外の流れの速度とほぼ一致する点までの距離を境界層の厚さ δ とすると，δ は流体の動粘性率 ν の 1/2 乗に比例する。たとえば，速度 U の一様な流れに平行に置かれた平板に沿う境界層では，板の前端から距離 x の点での厚さは， で与えられる。一例として，U＝10m/s として，x が 1mの点では，流体が空気 (ν＝0.145cm²/s) のとき δ＝0.6cm ，水 (ν＝0.114cm²/s) のとき δ＝0.17cm となる。レイノルズ数がある臨界値以上に大きくなると，境界層の中は乱流になり，流れの性質は一変する。また高速気流においては，境界層は流体の圧縮性と粘性発熱の影響を受け，超音速流では衝撃波との干渉が起る。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

境界層【きょうかいそう】

粘性の小さな流体（空気，水など）が物体に接して流れているときは，流れ全体を，物体表面に接し粘性が強く作用しているごく薄い層と，その外をとりまく完全流体の流れとに分けて考えることができる。前者を境界層という。境界層内では，物体表面に接するところでは流体の速度は０で，表面から離れるにつれて速度を増し，境界層の境で外の完全流体の流れにつながる。境界層外の流れが，物体表面に沿って下流ほど圧力が増すようになっていると，境界層は物体表面からはがれて渦(うず)をつくり，物体は強い抵抗（圧力抵抗）を受けるようになる。境界層の概念は1904年プラントルが考え，流体力学ではきわめて重要である。
→関連項目境界層制御装置｜流線型

出典　株式会社平凡社

世界大百科事典（旧版）内の境界層の言及

【渦】より

…一般の渦運動では流体の各点のまわりにこのような回転運動があり，ベクトルとしての渦度は場所ごとに変化する。粘性が小さく渦のない流れでも，その中におかれた物体の表面では流れが静止するために，流れに垂直な軸をもつ渦の集中した薄い層(境界層)が表面に存在する。このような渦層は速さの異なる二つの平行流の界面にも現れる。…

※「境界層」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」