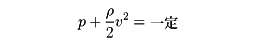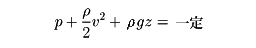翻訳｜flow
［名］
［接尾］助数詞。旗・Sponserd by 
液体と気体は固有の形をもたず自由に変形するので、その運動の仕方も固体とは非常に異なっている。そのため、日常的にも液体や気体の運動は「流れ」とよばれる。そして、液体と気体を一括して流体という。
流れについてわれわれ人間に興味があるのは、(1)流体はどのような運動をするか、(2)流れの中に置かれた物体は流れからどんな力を受けるか、(3)流れの中で物体はどんな運動をするか、などである。たとえば、川の水はどう流れるか、建物の周りの風速分布はどうか、などは(1)の例である。帆船に働く風の力、飛行機の翼に働く揚力、暴風によって建物の受ける破壊力などは(2)の例である。空中をひらひら落ちる木の葉、水中を泳ぐ魚、空を飛ぶ鳥、などの運動は(3)の例である。(1)(2)(3)の問題は独立なものではなく、(2)を知るには(1)が、また(3)に答えるには(1)と(2)の知識が必要である。
流体は変形しながら運動するので、その運動、つまり流れはきわめて複雑である。しかし、簡単な流れを調べておくと、複雑な流れについてもそのようすをある程度理解し予測することができる。
［今井 功］
流れのなかでもっとも簡単なものは管を通る流れである（）。管の断面積をS、流速をv、流体の密度をρとすると、断面を通って単位時間当りに流れる流体の質量はρvSである。この値は、管のどの断面をとっても同じである。すなわち
ρvS＝一定
の関係が管の各断面について成り立つ。これを連続の条件という。液体については密度は一定であるから、この条件はvS＝一定となる。すなわち流速vは断面積Sに反比例して変化する。これは常識的にわかりやすい事実である。
管の中で流速が変化すると、それに応じて流体の圧力pも変化する。その関係は、縮まない流体の場合
の公式で表される。これをベルヌーイの定理という。すなわち、圧力の高いところでは流速が小さく、圧力の低いところでは流速は大きい。これは、高圧のところから低圧のところへ流体が加速されると考えれば納得できることであって、エネルギー保存の法則に相当するものである。管が水平から傾いている場合には重力の影響が付け加わって、ベルヌーイの定理は
となる。zはある基準面から測った高さで、gは重力の加速度である。
［今井 功］
静止流体中を物体が運動すると、それによって流体も運動する。すなわち流れが生ずる。もっとも簡単なのは物体が等速運動をする場合である。見方を変えると、これは静止物体に一様な流れが当たる場合に相当する。それゆえ、飛行機や船が空気や水から受ける力を研究するために、風洞や水槽で空気や水の一様な流れをつくり、その中に模型を置いて、模型の周りの流れを調べるという方法が使われる。
簡単な物体の代表的なものとして、円柱に一様流が当たる場合を調べると、次の事実がわかる（）。(a)流速の遅い場合、流れのようすは前後・左右ともに対称である。(b)流速をすこし増すと、前後対称性は破れ、下流側では上流側より流線間隔がやや広がってくる。(c)さらに流速を増すと、円柱表面に沿う流線は途中ではがれて円柱の背後に渦の目玉が現れる。(d)流速を増すにつれて、渦の目玉は長く伸び、左右に振動を始める。(e)ある流速に達すると、渦の一つは円柱背後から離れて吹き流される。それとともに相手側の渦は成長を始めて、ついに吹き流される。この現象が次々とおこるために、円柱の背後に美しい渦の列ができる。これがすなわちカルマン渦(うず)である。(f)さらに流速を増すと渦の放出は頻繁になり、渦は混ざりあって円柱背後の流れは時間的にも空間的にもきわめて複雑・不規則に変化する。さらに流速を増してもこの状態は変わらない。このように、円柱という簡単な形の物体についても、その周りの流れは流速によって複雑に変化する。しかし、この複雑な変化も、レイノルズ数という無次元の数を導入することによって統一的につかむことができる。流体の密度をρ、流体の粘性率をμ、一様流の速度をU、円柱の直径をLとすると、R＝ρUL/μは無次元で、レイノルズ数とよばれる。一定の円柱（Lは一定）、一定の流体（ρとμは一定）についての実験ではRはUに比例するので、Rはいわば無次元の速度である。の(a)(b)(c)(d)(e)(f)につけたRの値は、それぞれの現象についてのRの概略値を示す。図の現象は円柱の大小に関係せず、また水、油、空気など使用する流体の種類によらず共通してみられる現象なのである。
飛行機の翼の断面形や胴体の形は流線形とよばれている。このような物体に一様な流れが当たる場合を調べると、のように、流れの全般的なようすは流速によってほとんど変化しない。しかし、流速分布を調べると、Rの値によって非常に異なることがわかる。たとえば、直線AA'上の流速の分布は、R＜1ではほとんど直線的に変化するのに対して、R＞1000では物体の表面近くで急に0まで下がる。そのようすを拡大して示したのがである。その流れのようすは、(1)に示すような2枚の平板の間に流体を挟み、一方の板を他方の板に平行に動かすときの流れに似ている。その流れはまた、(2)のように2枚の板の間に丸棒を挟んで一方の板を動かすときの棒の運動とも似ている。つまり、(1)の流体の平行なずれ運動は、実は流体の各部分がころのように自転運動をしながら並進運動をしているのである。自転運動をしている流体部分がすなわち渦である。(b)の物体表面を覆う流速の急変する薄い層は境界層とよばれるが、これはつまり渦の層にほかならない。
一般に、物体に流れが当たるとき、Rの大きい場合、流れの場は、(1)物体の上流側から側方に広がる滑らかな流線模様を示す領域、(2)物体表面を覆う境界層、(3)物体背後の複雑な渦運動をする領域、の三つに分かれる。(1)は主流、(3)は伴流とよばれる。とくに、境界層が途中ではがれず、したがって伴流がきわめて狭いような物体が流線形である。流線形でない物体は鈍い物体とよばれる。
はがれた境界層は渦の層として行動し、巻き上がって孤立した渦巻をつくり、あるいは分裂して大小さまざまの渦の群をつくる。これが、(e)のカルマン渦や(f)の複雑な渦領域の発生する原因である。複雑な不規則な流れを乱流、これに対して滑らかな流線をもつ流れを層流という。
［今井 功］
一見複雑にみえる流れも、その各部分を観察すると、前述の管の中の流れと物体の周りの流れの知識をもとにして考察することができる。たとえば、滑らかな流線がみられる部分では、流線を壁とする管、すなわち流管の中の流れと考えられるから、流管の細い部分、つまり流線間隔の狭い場所では流速が大きく、したがってベルヌーイの定理により圧力が低いことがわかる。また流れのようすは、空気、水、油、水銀のように、流体の密度や粘性によって異なるのはもちろん、流速や物体の大きさによっても千変万化するように予想されるが、実はレイノルズ数R＝ρUL/μ（Lは物体の代表的な長さ）だけで決まることは重要である。水や空気の粘性は小さいので、日常経験する流れではRはきわめて大きい。したがって、(f)の伴流のような不規則な渦運動をする領域がかならず現れるのである。すなわち、乱流現象は大きいレイノルズ数Rの流れではとくに重要な意味をもつのである。しかし、Rの小さい流れでは、の(a)、(b)で示されるように、境界層は現れず、流線は至る所滑らかであるから乱流はおこらない。これは粘性の影響が大きい場合に相当する。たとえば、空気中や水中を運動する微生物にとっては、空気や水は極度に粘い液体のように感じられるだろう。
普通の速度では気体と液体の流れについて違いはない。しかし気体では、流速が場所によって変化すると、ベルヌーイの定理によって圧力も変化するので密度も変化する。それゆえ、密度変化をしない液体とは異なった運動をする。そのような相違が現れるのは、流速vが気体中を伝わる音波の速度の半分程度以上になる場合である。そのような気体の圧縮性が無視できない流れを高速気流という。低速の流れでは気体でも液体でも流れ方に相違はないのである。
［今井 功］
『A・H・シャピロ著、今井功訳『流れの科学』（1977・河出書房新社）』▽『木村竜治著『改訂版 流れの科学』（1985・東海大学出版会）』▽『有田正光著『流れの科学』（1998・東京電機大学出版局）』▽『古川明徳・瀬戸口俊明・林秀千人著『流れの力学』（1999・朝倉書店）』▽『矢川元基編『パソコンで見る流れの科学――数値流体力学入門』（2001・講談社）』▽『澤本正樹著『流れの力学――水理学から流体力学へ』（2005・共立出版）』
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by
水や空気で代表される液体や気体は固体と異なり，一定の形をもたない。そしてわずかな圧力で容易に変形し，その運動を続ける。このため，液体と気体を総称して流体と呼び，その運動を流れという。流体やその静止・運動の状態，流体がその中におかれた物体に及ぼす力などを研究する学問が流体力学である。流体とは気体と液体との総称であると述べたが，固体のように見えるものでも，プラスチック，アスファルト，地球のマントルなど，長い時間，大きな空間のスケールで見れば流れの性質を示すものもある。一般に，空間内にとった各点の動きを，時間のような一つのパラメーターの連続関数として記述できるとき，これを抽象化して流れということもある。
流れを具体的に見るためには，一般には流体とともに移動する微粒子（おがくず，アルミ粉など）や気泡などのトレーサーを用いる。時間的に変わらない流れ（定常な流れ）ではこれらを写真撮影すると一定の筋模様が見られる。それを作る曲線は，接線をとればその瞬間における接点での流れの速度の方向を与える。このように，その上の各点での接線の方向が，その点での流れの方向と一致するような曲線を流線という。定常な流れでは，流線は流体の各実質（流体粒子）のたどる道筋を表しており，流れの道筋または流跡と考えることもできる。時間的に変動する流れでは瞬間露出と継続露出とで撮影の映像が異なり，前者は流線，後者は各瞬間での流線の包絡線である流れの道筋を与える。また煙突から出る煙のすすや水に流した色素が見せる筋模様は，特定の点から次々に出てくる流体粒子をつないだもので，色つき流線とか流脈と呼ばれる。流線，流れの道筋，色つき流線は定義からもわかるように別々のものだが，定常な流れでは全部が一致する。
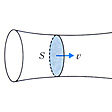
流れの中に小さな閉曲線をとれば，その各点を通過する流線は一つの管を作る。これを流管という。定常な流れでは流管の形は変化することはなく，流体は流管に沿って流れると考えることができる。縮まない流体では，流管内のある断面を単位時間に通る流体の質量はどこでも一定である。その質量は，断面積をS，流体の密度をρ，速度をUとすれば，ρUSで与えられ，流管の細い，言い換えれば流線の密集しているところほど流れの速度は大きいことがわかる。
なお，その定義からもわかるように，観測者が移動すると流れとの相対速度によって流線の形は異なる。
流れの中に小さな球状の流体のかたまり（流体粒子）を考えると，その運動は，（1）中心の速度vでの並進運動，（2）角速度Ωでの回転運動，（3）球が楕円体に変形するような変形運動とに分けることができる。（1）と（2）とはそれぞれ流体の運動量，角運動量に対応するものである。（3）はさらに等方的な伸び縮みという体積変化と，それを除いた純粋のひずみ（ずれ）運動とに分けることができる。並進運動以外の運動の速さはいずれも球の中心での速度のこう配を適当に組み合わせたものである。
角速度Ωの2倍，ω＝2Ωを渦度と呼ぶが，そのような回転をもたない流れを渦なしの流れ，それが分布した流れを渦ありの流れという。とくに流体粒子の回転軸を次々に連ねてできる曲線を渦線という。また渦ありの流れの中にとった小さな閉曲線の各点を通る渦線の作る管を渦管と呼ぶ。
流体の中に任意の面をとると，両側の流体はその面をとおして互いに力を及ぼしあっている。これを応力といい，強さは単位面積当りの力で測る。静止しているふつうの流体では，応力は面に垂直で，互いにおしあう力（圧力）であって，その強さが面の方向によらない等方的な力である。これを静水圧という。流れが起こると力の等方性が破れ，面に並行な力，すなわちずれの応力（粘性応力）が現れて，流速を均一にしようとする。このような性質を流体の粘性という。粘性応力は，純粋なひずみの速度に物質によって定まる比例定数（粘性率）μをかけたものであり，流れの方向にx軸，それに直角な方向にy軸をとると，y軸に直角な面のx方向に働く粘性応力τは，流れの速度をUとして，τ＝μ（dU/dt）で与えられる。このような性質をもつ流体はニュートン流体と呼ばれ，またこのような流れ（ニュートンの流れ，ニュートン流動）を支配する方程式をナビエ=ストークスの方程式という。
→渦 →粘性
さて物体を過ぎる流れや管の中の流れなど，境界のある流れでは，境界の形や配置が同一であっても，流体の密度ρ，粘性率μ，流速（代表速）Uや代表的長さLなどによって流れの模様はさまざまである。しかし，自由表面がなく密度があまり変わらない定常的な流れでは，流体の慣性的な力ρU2L2と粘性による力μULとの比であるレーノルズ数Re＝ρUL/μが同じならば相似（レーノルズの相似則）が成り立ち，模型実験や数値計算に利用される。
ふつうのスケールでの水や空気の流れではReが非常に大きく，物体面などを除けば圧力の効果に比べて粘性による応力の効果を無視できる場合が多いので，理想化して粘性のない流体，すなわち完全流体を考え，その流れを議論するのが便利である。縮まない完全流体の定常な流れではベルヌーイの定理が成立する。また完全流体では渦の発生，消滅がないので，流線形の物体のまわりの流れなど，渦なしの流れで近似できる場合が多い。ただこれだと定常な流れの中におかれた物体に働く抵抗を説明できない（ダランベールのパラドックス）し，物体面での粘着条件を満足できないので，面に並行な速度の急激な変化をとり入れ，粘性が無視できないために生ずる渦の層，すなわち境界層を考える必要がある。また流線形以外の物体では，境界層がはがれて渦が離脱するとなかなか消滅せず，物体の後方に流されて乱れた伴流を形成し，圧力を下げるので大きな抵抗の原因になる。
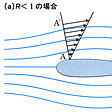
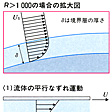
逆に粘性が大きかったり，物体の大きさが非常に小さい場合にはReが小さく，少なくとも物体の近傍では慣性の影響を無視することができ（このように慣性の影響を無視した流れをストークスの流れという），対称な物体では前後対称の流れが得られる。ストークスの流れの存在する領域は渦で満たされた領域であるが，代表的な長さとして物体からの距離でとったレーノルズ数が大きい領域では渦が後方に流され，粘性によって広がって放物線状の伴流を形成し，その外側に渦なしの領域が存在することになる。一方，細い管の中の流れや土のような多孔質の中の流れ（浸透流）は，全領域でReが小さいとみなすことができる。
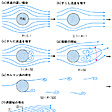
Reが大きくなると流れの前後の対称性はしだいにくずれていく。もちろん円弧のような物体ではRe＝0でも凹部に目玉状の回転流があるが，例えば円柱のような物体でもReが5程度を超えると，背部に上下対称の1対の目玉状の回転流が現れ，それがReの増大とともにしだいに後方にのびていくと流れの上下の対称性も破れ，交互に渦が離脱して規則正しい渦の列（カルマン渦列）が形成される。さらにReを増すと，規則性が破れて前にも述べたように乱れた伴流に移行する。このようにReが小さいときの整然とした流れ（層流）が，Reの増加とともに不規則に変動する流れ（乱流）に移行するのは，移行のしかたこそ異なれ，流れの一般的な特徴であり，O.レーノルズが円管の中の乱流について初めて明らかにした（1883）ものであるが，その移行は同心回転円筒間の流れ（テーラーの流れ）や熱対流のほうがゆるやかでわかりやすい。
高速の気体の流れ（高速気流）では，速度の変化による圧力の変化が大きくなると密度一定と考えることができなくなる。音速をcとするとき，マッハ数M＝U/cがその目安であって，Mが小さければ気体でも密度変化を無視できるが，Mが大きくなると，流れの速度が遅くても物体の近傍に局所的に超音速の領域が形成されるようになる。超音速の流れでは音の速さで球面状に広がっていく微小かく乱が流れによってそれよりも速く下流に流され，円錐状のマッハ波を作るばかりでなく，一般に有限のかく乱では不連続的な衝撃波が形成されるので，マッハ数が1の近傍の流れは複雑である。またMが1よりずっと大きくなると，発熱による解離，電離発光など物性の変化が無視できなくなる。
→高速気流
自由表面がある場合は重力や表面張力の影響で，また高さによる密度や温度差のある場合には浮力や拡散の影響で，さらに回転のある場合にはコリオリの力の影響により，流れに波動が出現したり，対流などの循環流やさらに乱流や沸騰などを伴う複雑な流れも生じうる。これらの現象は船舶や航空機の運行や流体機械，化学装置などに深く関連するものであるが，さらに海岸や大気・宇宙空間における海流や潮汐，大気大循環，気象変動，太陽風の発生，天体の構造，銀河の運動など，流れとして把握できるものが多い。また電離した気体（プラズマ），地球内部のマントルのような液状金属などでは，磁場中の運動による起電力のために電流が生じ，磁場によって力を受けるなど電磁場とのかかわりが大きく，電磁流体力学の対象となる。
初めにも述べたように，固体の流れやコロイド溶液など化学的に複雑な物質の流れでは，応力と変形の速度との間の関係も複雑で，一括して非ニュートン流れ（非ニュートン流動）と呼ばれ，いわゆるレオロジーの対象となる。一般に固体粒子群の浮遊する液体，気泡を含む水など，異なった相をもつ物質の混合物の流れを全体として見るときは混相流と呼ぶこともある。
執筆者：橋本 英典
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by
Sponserd by
…経済学の概念。〈私の所得は100万円である〉という表現は不十分である。というのは，100万円が日収か月収か年収かで意味が異なるからである。このようなことが起こるのは，同じ所得水準であっても，時間を計る単位を変更することによって，所得の大きさが変わってしまうからである。所得水準のように，または河の流量や速度のように，時間を計る単位を変更することで値の変わる変数，したがって単位時間を明示して示さねばならない変数をフロー変数と経済学では呼ぶ。…
※「流れ」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
Sponserd by
その議会の過半数には達しないが、議席数をもっとも多くもつ政党。...
