数学的構造（読み）すうがくてきこうぞう（英語表記）mathematical structure

日本大百科全書(ニッポニカ)

数学的構造
すうがくてきこうぞう
mathematical structure

数学でよく用いられる重要な概念で、たとえば順序、群、環、体(たい)、位相空間とか測度などが、どのような関係や算法によって組み立てられ、構造をなしているか、また、それらの差異や類似性がどのようになっているかの仕組みを明らかにしようとするものである。

　ここでは整数の全体Zを例にとり、まず順序構造について説明しよう。Zの上には3≦5というような大小関係≦がある。そして、すべてのZの元について次のような性質が満足されている。すなわち、(1)a≦a（反射律）、(2)a≦b, b≦aならばa＝b（反対称律）、(3)a≦b, b≦cならばa≦c（推移律）およびa≦bまたはb≦aが成立する。この順序関係に対して集合｛(x, y)|x≦y｝を考えれば、これはZの順序対の集まり、すなわちZの直積Z×Zの部分集合を定める。これを関係≦のグラフとよぶ。また関係≦をZから真偽値への写像と考えることもできる。すなわち真を1、偽を0で記し、その集まり2＝｛0, 1｝を考えれば、≦は写像として、≦：Z×Z→2である。このように一つの集合Aと、その上の二項関係Rの組（A：R）について性質
　　aRa
　　aRb, bRa→a＝b
　　aRb, bRc→aRc
がAのすべての元について成立するとき、この組（A：R）を部分順序構造、またさらに、aRbまたはbRaが成立するときに線形順序構造とよばれる。Zの場合はさらに5＋(－2)＝3のように0および算法－、＋があって次のような性質が満足されている。すなわち
　　a＋0＝0＋a＝a（単位元）
　　a＋(－a)＝(－a)＋a＝0（逆元）
　　a＋(b＋c)＝(a＋b)＋c（結合法則）
　　a＋b＝b＋a（交換法則）
が成立している。このように集合Aと、その元e、1変数の写像（′）、2変数の写像（＊）すなわち′：A→Aと＊：A×A→Aの組(A：e, ′, ＊)について性質
　　a＊e＝e＊a＝a；a＊a′＝a′＊a＝e；a＊(b＊c)＝(a＊b)＊c
がAのすべての元について成立するとき、この組を、群構造を有する、または単に群であるという。さらにa＊b＝b＊aが成立するときアーベル群または可換群という。この場合には、通常e、′、＊のかわりに0、－、＋が用いられている。さらに、Zでは、1と乗法×があって(2＋3)×5＝2×5＋3×5のように、
　　a×1＝1×a＝a（乗法の単位元）
　　a・(b・c)＝(a・b)・c（結合法則）
　　a・(b＋c)＝a・b＋a・c, (a＋b)・c＝a・c＋b・c（分配法則）
が成立する。このような場合、組(A：0, －, ＋, 1, ×)は環構造を有するとか、単に環であるという。通常はこのような定数0、1とか写像－、＋、×を明記しないで、Aは群であるとか環であるとかいうが、この場合、文脈から算法＋とか×が明らかな場合である。

　また、たとえば位相空間の場合でも、いろいろの定義、すなわち近傍系、開集合族とか閉包によるものがあるが、閉包を用いて記述すれば、集合Aと閉包の写像￣：P(A)→P(A)（P(A)はAのべき集合、すなわちAの部分集合の全体）に対して性質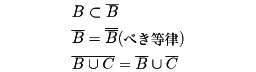

がAのすべての部分集合について成立するとき、(A：￣)を位相構造または単に位相空間などとよぶ。

　このように何個かの基本的集合とその間の写像との関係と、それらの元の間に成立する関係（通常公理とよばれる）を具体的に述べたものを数学的構造とよんでいる。

［難波完爾］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

数学的構造 (すうがくてきこうぞう)
mathematical structure

数学では扱う対象を集合としてとらえるのがふつうである。その場合，扱われるものは単なる集合ではなく，何らかの数学的性質が付与されたものであるのがふつうである。その付与された性質を数学的構造，または単に構造という。以下に例示するようにいろいろな場合がある。

（1）順序集合には，その元の間の大小関係が与えられている。その大小関係が数学的構造の一例である。

（2）群は一つの算法をもつ集合で，その算法についてのある条件が満たされるものである。このときの付与された算法は数学的構造の一例である。

（3）環や体は加法と乗法という2算法をもつ集合で，その算法についての，いくつかの条件を満たすものである。このときの2算法が数学的構造の例になる。

（4）ベクトル空間は加法という算法をもつベクトルの集合Vのほかに，スカラーと呼ばれる元のなす体Kが与えられていて，ベクトルのスカラー倍という算法も定義されていて，この算法およびベクトルの加法とがいくつかの条件を満たすものとして定義されている。したがって，この場合の数学的構造は，ベクトルの加法，スカラー全体の作る体K，スカラー倍の算法の三つをあわせたものによって与えられていることになる。

（5）位相空間は集合に位相が与えられたものである（位相を定めるのには，開集合を定める方法，閉集合を定める方法，各点の近傍を定める方法などがある）。この場合の位相は数学的構造の一例である。

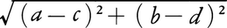（6）距離空間は，その2点の組おのおのについて，距離が与えられている。この距離は数学的構造の一例である。距離によって位相が定まり，位相空間と考えられるが，距離を与えることは，それによって定まる位相を与えることよりも，多くのことを与えている。例えば平面上において，2点（a，b），（c，d）の距離を，と定めた距離空間と，他の距離｜a－c｜＋｜b－d｜によって距離空間にしたものとは，位相は同じであって，距離はだいぶ違う例である。
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

数学的構造
すうがくてきこうぞう
mathematical structure

単に構造ともいう。数学の一つの理論は，ある全体集合の元 (要素，対象，個体，変数) の間に，基本的な関係，すなわち公理を規定することによって成立する。このように，公理による元の間の関係の規定を，数学的構造という。たとえば集合 G の2元 a ，b に1つの結合演算 a・b(a，b∈G) が規定されていて，この結合演算に関して，(1) a・b∈G ，(2) a・(b・c)＝(a・b)・c ，(3) すべての a∈G に対して，a・e＝a となる e∈G がただ1つ存在する，(4) 各元 a∈G に対して a・a'＝e となる a'∈G がただ1つ存在する，という4条件 (公理) が与えられているとき，G は一つの数学的構造をもち，これをわれわれは群と呼んでいる。環や体，線形空間や位相空間，多様体などはそれぞれ一つの数学的構造である。

出典　ブリタニカ国際大百科事典 小項目事典