運動エネルギー（読み）ウンドウエネルギー

デジタル大辞泉

うんどう‐エネルギー【運動エネルギー】

運動している物体のもつエネルギー。速度vで運動している質量mの物体（質点）の運動エネルギーはmv²/2である。

出典　小学館

精選版 日本国語大辞典

うんどう‐エネルギー【運動エネルギー】

1. 〘 名詞 〙 ( エネルギーは[ドイツ語] Energie ) 運動中の物体がもつエネルギー。大きさは、質量とその物体の速度の二乗に比例する。
   1. [初出の実例]「気体運動論に於ては分子運動の運動エネルギーに由り」(出典：学生と教養（1936）〈鈴木利貞編〉学生時代の回顧〈東畑精一〉五)

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

運動エネルギー
うんどうえねるぎー

速度vで運動している質量mの質点は、同じ位置で静止しているときよりも(1/2)mv²だけエネルギーを多く有している。このエネルギーを運動エネルギーという（図A）。

　質点の集まり、すなわち質点系の運動エネルギーは、各質点の運動エネルギーの和になる。この場合、質点系の質量中心の運動エネルギーと質点系内の相対運動の質点エネルギーとの二つの項に分けることができる。広がりをもつ物体の場合には、物体を質量Δmの微小な部分に分け、各部分の運動エネルギー(1/2)Δmv²の総和をとれば、広がりをもつ物体の運動エネルギーを求めることができる。この場合、速度vは一般に物体の各部分ごとに異なる。物体が剛体とみなしてよい場合には、物体全体の運動を質量中心の運動と、質量中心を通る一つの決まった軸の周りの物体の回転運動とで表すことができる。物体の回転軸の方向は一般に時々刻々変化している。各瞬間における回転軸の周りの剛体の回転の速さ、すなわち角速度をω、剛体の全質量をM、質量中心の速度をvとすれば、その運動エネルギーは

となる。I₀は、剛体の密度分布とこの瞬間の質量中心を通る回転軸の方向とで定まる量で、慣性モーメントという。この表式は剛体の各部分の運動エネルギーを総和して得られる。

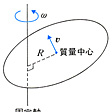
　剛体が図Bのように一つの固定した軸の周りを角速度ωで回転しているとき、その運動エネルギーは、固定軸の周りの質量中心の回転運動のエネルギーと、質量中心を通る軸の周りの剛体の回転運動のエネルギーとの和になる。両方の回転とも角速度はωに等しく、質量中心を通る回転軸は固定軸に平行である。質量中心の速度をv、質量中心と固定軸の距離をRとすると、v=Rωであり、回転運動のエネルギーTは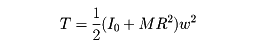

となる。I=I₀+MR²は回転軸の周りの慣性モーメントであって、これを用いると運動エネルギーは

となる。相対性理論では、静止質量m₀の質点が慣性系に対してvの速度を有するとき、その全エネルギーは

となる。cは光の速さである。したがって、この場合の運動エネルギーは、全エネルギーから速度によらない静止エネルギーm₀c²を除いた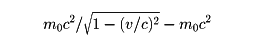

となる。vがcに比べて小さいときには、この値はほぼ（1/2）m₀v²という非相対論的な場合の運動エネルギーに等しくなる。

［田中　一］

[参照項目] | 剛体 | 質点

運動エネルギー〔図A〕

運動エネルギー（剛体の回転）〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

運動エネルギー (うんどうエネルギー)
kinetic energy

運動する物体は仕事をする能力をもつ。この能力は物体が止まるまでになしうる仕事の量ではかられるが，物体の質量m，速さvを用いると，1/2mv²と表される。これを物体の運動エネルギーという。ここで物体のする仕事の量とは，物体がそれに働いている力に逆らって移動する距離sと，その方向に逆向きに働いている力の大きさFとの積Fsのことである。力Fとsの向きが同じときには，逆に力（または力を及ぼしている物体）がその物体に対して仕事をしたという。（1/2）mv²が物体のなしうる仕事を表すことは，例えば，物体を速度vで地上のある高さまで投げ上げることを考えてみるとわかる。このとき物体が止まるのは最高の高さhに達するとき，すなわちv/g秒後（gは重力の加速度）であり，高さhは（1/2）v²/gに等しい。この間に物体は自分自身を重力mgに逆らってhの高さまでもち上げる仕事mghをしているが，この大きさがちょうど（1/2）mv²になっている。物体が外力によって仕事をされるときは，その仕事の量だけ運動エネルギーが増し，逆に物体が外部に仕事をするとそれだけ運動エネルギーは減少する。物体が回転しているときには運動エネルギーとして回転のエネルギーも考えなくてはならない。これは回転軸のまわりの慣性モーメントIと軸のまわりの角速度ωを用いて（1/2）Iω²の形で与えられる。なお，相対論的力学では質量mとエネルギーEの間の関係式として，アインシュタインの関係式と呼ばれるE＝mc²（cは光速）がある。m₀を静止質量とすると，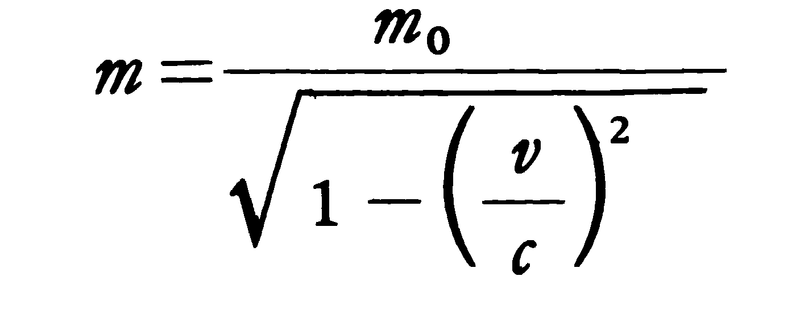

だからEはvがcに比べて十分小さいとき近似的にm₀c²＋（1/2）m₀v²となる。第1項は静止エネルギーと呼ばれる。第2項が古典力学の運動エネルギーである。したがって，ニュートン力学の運動エネルギーは，vが光速に比べて十分小さいときの相対論的エネルギーの近似値だということができる。
→エネルギー
執筆者：田辺 行人

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

運動エネルギー
うんどうエネルギー
kinetic energy

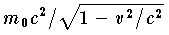速さ v で運動する質量 m の物体は，静止するまでに他に対して mv²/2の仕事ができる。 mv²/2をこの運動物体がもつ運動エネルギーという。角速度ωで回転運動する物体の回転軸に関する慣性モーメントが I ならば，この物体がもつ回転の運動エネルギーは Iω²/2である。相対論的力学では，光の速さを c とすれば，静止質量 m₀，速さ v の物体は相対論的エネルギー をもつ。物体は静止（v＝0）のときでも静止エネルギーm₀c²をもつから，運動しているための余分のエネルギーが運動エネルギー K であって，K は次式で与えられる。
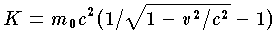v が c に比べて十分に小さいときは K≒m₀v²/2となり，ニュートン力学での値に一致する。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

運動エネルギー【うんどうエネルギー】

運動する物体は仕事をする能力をもつ。この能力は物体が止まるまでになしうる仕事の量ではかられる。質点の質量をm，速度をvとするとmv²/2をいう。ある時間内の質点の運動エネルギーの増加は，その間に質点に働く力のした仕事に等しい。一般の物体の運動エネルギーはそれを構成する質点の運動エネルギーの和に等しく，その増加は各質点に働く力のした仕事の和に等しい。→位置エネルギー／力学的エネルギー
→関連項目気体分子運動論｜コリオリ

出典　株式会社平凡社

世界大百科事典（旧版）内の運動エネルギーの言及

【エネルギー】より

…例えば，S.ステフィンはこれを自明のこととして用いて，力の合成の平行四辺形則を証明している。　しかし，エネルギーの概念の萌芽となった運動エネルギーに関する考察を初めて試みたのは，やはりG.ガリレイであった。彼は1600年ごろ，木材の上に立てた釘の頭に金づちの頭よりずっと重い物を載せても釘は木の中に入らないが，金づちを振り上げて打つだけでなぜ釘は楽に木材に打ち込まれるのかを問題にし，運動する物体には何か固有の“ちから”があると考えた。…

【回転運動】より

…外力がないか，あっても作用線が回転軸を通る場合には，Lは一定に保たれる。これらの関係は，並進運動の運動法則における質量，速度，運動量，力をそれぞれ慣性モーメント，角速度，角運動量，力のモーメントに置き換えたものに対応しており，運動エネルギーもで与えられる。並進運動の慣性に対応するのは，全角運動量Lあるいは角速度ωを一定に保とうとする性質であり，これを利用すると慣性モーメントの大きいはずみ車を用いてエネルギーを蓄えることが可能である。…

※「運動エネルギー」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」