ブラウン運動（読み）ブラウンウンドウ（英語表記）Brownian movement

デジタル大辞泉

ブラウン‐うんどう【ブラウン運動】

気体や液体中の微粒子の不規則な運動。周囲の熱運動をする分子の衝突が不均一なために起こる現象で、R＝ブラウンが水中での花粉の運動から発見。のちアインシュタインとランジュバンにより理論化された。

出典　小学館

精選版 日本国語大辞典

ブラウン‐うんどう【ブラウン運動】

1. 〘 名詞 〙 ( ブラウンはBrown ) 微小な物体の示す無秩序な熱運動。一八二七年、イギリスの植物学者ロバート=ブラウンが水中に浮く花粉の示す不規則な永久運動を発見し、はじめ花粉の生命と結びつけたが、これは無機物でも起こっており、後、真の原因は周囲の媒質の分子の熱運動による衝突であることがわかった。〔原子の構造（1924）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

ブラウン運動 (ブラウンうんどう)
Brownian movement

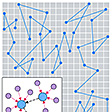
花粉を水に浮かべておくと，破裂してたくさんの微粒子が出てくる。それを顕微鏡で見ると，ぴりぴり，ぶるぶると活発に動きまわっている。この運動を初めて観察したのはイギリスのニーダムJohn Tuberville Needham（1713-81）で，1740年のことといわれているが，当時はこの動く微粒子が動物の精子にあたるのだろうと考えられていた。その後，1826年になって，イギリスの植物学者R.ブラウンがこの動く微粒子の運動をもっとよく調べようとした動機も，植物の受精の研究だった。微粒子の運動が水の対流や振動にひきずられて起こっているのだとは思えない。微粒子がスーッと動いて他の微粒子に引き寄せられていったかと思うと，またスーッと離れていくのは，水の動きに引きずられているとしたのでは理解できない。ブラウンも初めは微粒子に生命があってその意志で動いているのだと考えた。しかしそうだとしたら，微粒子を殺してしまえばこの運動はなくなるはずである。ところが死後長い年月を経た植物から採取した微粒子も，アルコールづけにしておいた微粒子も，生きた植物からとったものと同じように運動する。彼はさらに石炭やすすから採集した微粒子を水に浮かべて顕微鏡で見たが，やはり同じだった。しかしこれらも有機物なので，彼は次に岩石や金属の微粒子（直径が1μmくらい）を水に浮かべてみたが，やはり活発に，そして互いに独立に動き回っていた。すなわち，この運動は物質の種類にはよらない。静止した液体や気体の中にある微粒子のこのような不規則な運動を彼の名にちなんでブラウン運動と呼ぶ。ブラウン運動を手軽に見るには，清水に少量の牛乳を滴加して白色の乳濁液を作り，顕微鏡（倍率200倍以上）で見ればよい。水中に浮いている牛乳の脂肪の微粒子のブラウン運動が見られるだろう。

機構

液体を構成している分子は，まったく静止した熱平衡状態にある液体中でも，激しく熱運動している（水の場合，分子の熱運動の速さは550m/sほどもある）。これがボルツマンの統計力学の与える結果である。このような分子が微粒子にぶつかっても，分子1個の質量は微粒子のそれに比べて軽すぎるため，微粒子を動かすには力足らずである。しかし，微粒子が分子と分子の間隔に比べても非常に大きいため，どの瞬間を見ても，きわめて多数の分子があらゆる方向から微粒子にぶつかっている。ここでいう瞬間は，顕微鏡下で肉眼ないし高速度写真で見た瞬間で，数学的な時間の1点ではなく，ある程度の幅をもっていることに注意しよう。もしも微粒子がもっと大きい粒子だとしたら，その粒子が分子との衝突で受けている力は平均していつでも0になってしまうだろう。これはまた熱平衡であらゆる動きが止まってしまうことの理由であった。大きさが1μm以下の微粒子になると，各瞬間に衝突する分子の数が減り，力の瞬間的平均は必ずしも0ではなくなり，ゆらぎが目だってくる。このゆらいでいる力によって微粒子は加速され，ブラウン運動を始める。ゆらぎは時々刻々と，でたらめに大きさも方向もかわる力であるから，ブラウン運動をしている微粒子の軌跡は，まるで酔いすぎた人の足どりのようにあてもない。

　ブラウン運動の存在は，次のようにすれば，直接肉眼でも確かめられる。ガラスの容器の中に閉じ込めた空気の中に，直径1μmくらいの細い水晶の糸で1mm平方くらいのごく薄い雲母片をつり下げる。その面を鏡にしておいて，これに決まった方向から弱い光線を当てて，その反射光をスクリーンに当てて眺めると，反射光のスポットはふらふらゆらいで見える。このゆらぎは雲母片の回転ブラウン運動による。

ブラウン運動の理論

ブラウン運動の激しさは，液体中の分子の熱運動に比べればはなはだしく緩慢であることはいうまでもない。しかしともかく分子の熱運動がブラウン運動の原因であるのだから，ボルツマンの時代はまったくの仮説にすぎなかった分子の熱運動なるものの手がかりが，ブラウン運動の研究によってつかめるのではないかと考えられ，20世紀の初頭になってにわかにブラウン運動の研究が活発になった。フランスのJ.B.ペランはゴム原液を水に滴加した乳濁液を顕微鏡で観察し，一つの微粒子について30秒ごとの位置を方眼紙に写してみた。時間tだけたつと微粒子がはじめの位置からrだけ離れたとして，r²の値をいろいろな微粒子について平均してみると，その値〈r²〉はtに比例していることが見いだされた。これはブラウン運動が数学上random walkと呼ばれる問題に帰着する証拠である。random walkはまた酔歩とも呼ばれ，これはまさに酔いすぎた男の足どりである。酔歩では彼が今どちらの方向に進もうとも，その場限りの判断によるもので，今までどう進んできたかとか，これからどちらにいきたいかなどはまったく考えていないとされる。

　ブラウン運動する微粒子を初め1ヵ所に集めておくと，それぞれがかってに動き回るので拡散していく。その拡散係数Dは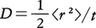，で与えられる。もしも液体が完全に静止していれば，重力のため個々の微粒子は長い間には沈降していくが，液体の粘性のため，沈降速度は微粒子に働く重力に比例する。この比例係数を微粒子の移動度というが，アインシュタインは，この移動度にk_BT（k_Bはボルツマン定数，Tは絶対温度）をかけたものがちょうど拡散係数Dに等しくなるというアインシュタインの関係式を発見した。この関係式を導くキーポイントは，微粒子も液体と熱平衡になったときは，その運動エネルギーが液体分子のそれと同じくボルツマンのエネルギー等分配則に従うということであった。アインシュタインの関係式が実証されたことによって，ボルツマンの分子運動論が間接的にではあるが実証されたことになった。

　ブラウン運動の理論はさらに，確率過程の例題として，より美しい数学的形式にみがき上げられていく。ポーランドのM.vonスモルコフスキー，ドイツのフォッカーAdriaan Daniël FokkerおよびM.プランク，フランスのP.ランジュバンによって発展され，さらにのちにはN.ウィーナーにより確率過程の数学の一部門にもなっていく。フォッカー=プランクの方程式は微粒子の位置と速度の確率分布関数がみたすべき方程式であり，ランジュバン方程式は微粒子の運動方程式で，速度の減衰項や外力（重力）のほかに，ランダム・ノイズとしてのゆらぐ力を含んでいる。分子衝突に起因するゆらぎの力は確率変数である。
執筆者：伊豆山 健夫

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ブラウン運動
ぶらうんうんどう
Brownian motion

流体（気体あるいは液体）中にあるコロイド粒子（直径がミクロン程度の粒子）が行う不規則運動。1827年、花粉から出た粒子の水中における運動を顕微鏡で観測していたイギリスの植物学者R・ブラウンにより発見された。ブラウン運動は、最初、生命現象と関係があると考えられ注目されたが、その後しだいに分子の熱運動によることがわかってきた。

　コロイド粒子に働く力は分子とのランダムな衝突に起因する。流体を構成する分子は非常に小さく、その運動を直接、顕微鏡などで観測することは不可能である。ブラウン運動は、分子の熱運動そのものではないが、それを目に見える形に表したものといえる。ブラウン運動は分子の熱運動を証拠づける一つの現象である。

　ブラウン運動に関する力学の立場からの考察はアインシュタインによってなされた。粒子の質量をM、速度をvとする。このとき、粒子に働く力として個々の時間に衝突する撃力の平均的効果として、速度を減ずる方向に働く摩擦力を－kvとし、それ以外をランダム力f(t)とする。これにより、粒子の運動方程式は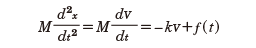

となる。このようにランダム力を含む運動方程式をランジュバン方程式という。ランダム力f(t)の性質として、ホワイト・ガウスノイズ（正規性白色雑音）とよばれるものが通常用いられる。これは
〈f(t)〉＝0,〈f(t)f(t´)〉＝2Dδ(t－t´)
を満たす。ここで<…>はさまざまなランダム過程に関する平均を表す。またここではランダム力間に時間的な相関がないとみなしている。この運動の定常状態では、速度の分布が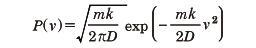

である。それが温度Tの熱平衡状態でのカノニカル分布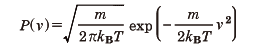

と一致するとすると
D＝k_BTk
の関係が導かれる。また、粒子の拡散係数はD_diff＝D/k₂で与えられる。これらの関係はアインシュタインの関係式とよばれる。この関係は、拡散係数と摩擦係数が独立ではないことを意味しており、揺動散逸定理とよばれるものの草分けとなっている。この式を利用すると、ブラウン運動の解析からボルツマン定数を実験的に測定することができる。

［宮下精二］

数学

ブラウン運動において、微粒子の時刻tにおける位置座標X(t)はtを含む確率変数と考えられる。数学的にはブラウン運動は次の確率過程として定式化される。すなわち確率空間Ωで定義された確率過程X(t,ω)で次の条件(1)、(2)、(3)を満たすものをウィーナー過程Wiener processという。以下X(t,ω)をX(t)と表す。

(1)X(t)∈R^d （＝d次元ユークリッド空間）
(2)t₁＜t₂＜……＜t_nである任意のt_i(i＝1,2,…,n)に対してX(t₂)－X(t₁),X(t₃)－X(t₂),……,X(t_n)－X(t_n-1)は確率変数として独立である。

(3)X(t)の第i成分をX_i(t)とするときX_i(t)(1≦i≦d)は独立であって、任意のt、sに対してX_i(t)－X_i(s)の確率分布は、正規分布N(0,|t－s|)である。

　このウィーナー過程をd次元ブラウン運動とよぶこともある。d次元ブラウン運動の道は確率1で連続であるが、有界区間でも有界変動ではなく長さをもたない。

［古屋　茂］

『飛田武幸著『ブラウン運動』（1975・岩波書店）』▽『米沢富美子著『ブラウン運動』（1986・共立出版）』▽『I・カラザス、S・E・シュレーブ著、渡邉寿夫訳『ブラウン運動と確率積分』（2001・シュプリンガー・フェアラーク東京）』

[参照項目] | アインシュタイン | コロイド | ブラウン | ボルツマン定数

ブラウン運動（コロイド粒子の不規則運動…

出典　小学館　日本大百科全書(ニッポニカ)

化学辞典 第2版

ブラウン運動
ブラウンウンドウ
Brownian motion, Brownian movement

水中に浮遊する花粉を顕微鏡で観察すると微小運動をしていることはかなり古くから知られていた．これは一種の生命現象と考えられたこともあるが，植物学者R. Brownはこの現象を詳細に研究し，生体物質に限らず有機・無機あらゆる物質の微小粒子に共通の物理現象であることを示した(1828年)ので，この運動にかれの名がつけられた．そののち多くの物理学者によって，この運動が，
(1)各粒子は互いに独立，
(2)不規則でつねに方向が変化し，
(3)対流，振動に無関係，
(4)媒質の粘度が小さいほど大きく，
(5)粒子が小さいほど活発，
(6)永久的であること，
などが確認され，この運動が液体分子の熱運動に関連するものと推定された．その後，A. Einstein(アインシュタイン)(1905年)は，コロイド溶液の拡散とこのブラウン運動との関係を理論的に考察して，関係式

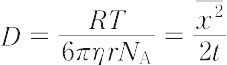
を導いた．ここで，Dは拡散係数，Rは気体定数，Tは絶対温度，ηは媒質の粘性係数，rは粒子(球形)半径，N_A はアボガドロ定数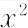，はt時間中に粒子が一定方向に移動する距離の自乗平均である．J.B. Perrin(ペラン)(1908年)は，単分散に近いコロイドを用い，粒子のブラウン運動を観察して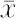，とt(30 s)との関係からアボガドロ定数 N_A を求めて妥当な値を得た．またR.A. Millikan(1911年)は，減圧気相中に浮遊する油粒子のブラウン運動を観察(油滴実験)して，精度の高い N_A の値を得るとともに，電気素量を測定した．Perrin(1926年)およびMillikan(1923年)は，これらの業績によりノーベル物理学賞を受賞した．あらゆる測定器の感度を極端に増大したときに現れる測定値のゆらぎは，ブラウン運動と同質のものであるとされている．

出典　森北出版「化学辞典（第2版）」

百科事典マイペディア

ブラウン運動【ブラウンうんどう】

気体，液体中に浮遊する微小粒子が行う不規則なジグザグ運動。1827年R.ブラウンが水中の花粉を顕微鏡で観察中に発見。熱運動をしている流体の分子が絶えず粒子に衝突し，粒子が大きいうちは衝撃が平均化されるため動かないが，微小な粒子では分子の衝突が少ないため平均化されず不規則な運動を生じる。アインシュタイン（1905年）とM.v.スモルコフスキー（1906年）が確率論に基づき，粒子がある時間後に移動した距離を温度，アボガドロ数等の関数として与える法則を確立。J.ペランは実験によりこの法則を証明，それからアボガドロ数を算出して分子の実在を明らかにした。
→関連項目アインシュタイン｜暗視野顕微鏡｜煙霧質｜コロイド｜スベドベリ｜分子

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

ブラウン運動
ブラウンうんどう
Brownian motion

熱運動などによって引起される物体の不規則運動。 1827年 R.ブラウンが水の中に入れた花粉から出た微小粒子の不規則運動から発見したとされている。希薄な気体中につるされた小さな鏡の不規則振動，電気回路の中の電流や電位差のゆらぎなど，観測される物理量はすべて物質の微視的な自由度のもつ熱運動に由来する同種のゆらぎをもっている。したがって，ゆらぎ自体が物質のミクロな性質解明の糸口を与える。ブラウン運動を記述する方程式としてはランジュバン方程式，フォッカー＝プランク方程式がある。 A.アインシュタインは，J.ペランによる金コロイド粒子のブラウン運動の観測をもとにして分子の存在を立証した。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

ブラウン運動【Brownian motion】

流体中に浮遊している微細粒子の示す不規則性運動．英国の植物学者ブラウンが花粉を水中に分散させたものを顕微鏡で観察していて発見した．粒子に対する統計的な圧力の揺らぎに起因する．よく「水中に分散した花粉粒の連続的な不規則運動」と記してあるテキスト類が少なくないが，ブラウン（R. Brown）の最初に観察したものは，花粉が水中で放出する微粒子であった．この理論的な解明はアインシュタインの貢献である．アインシュタインのブラウン運動の式＊を参照．

出典　朝倉書店

栄養・生化学辞典

ブラウン運動

　分子，原子，コロイド粒子などが液体中で動く状態．不規則な熱運動．

出典　朝倉書店

世界大百科事典（旧版）内のブラウン運動の言及

【ウィーナー過程】より

…初め，イギリスの植物学者R.ブラウンが顕微鏡で水中にある花粉から出る微粒子を観測しているうちに，それらが激しい不規則運動をしていることを発見した。この運動は，後に水の分子が微粒子と無数といってよいほど頻繁に衝突することによって起こるものであることがわかり，ブラウン運動Brownian movementと呼ばれるようになった。A.アインシュタインは，1905年にこの運動の数学的記述を与え，一定時間内の変移はガウス分布に従うことを理論的に示した。…

【アインシュタイン】より

…そこに7年間勤めたが，しごとの合間に行った理論物理学の研究は，20世紀物理学の基礎を築くことになった。すでに1901年から熱力学および統計力学に関する論文を発表していたが，05年に光量子仮説，ブラウン運動の理論，特殊相対性理論という，根本的かつ革命的理論を立続けに提出したのである。そのため，この年は〈奇跡の年〉といわれる。…

【アインシュタインの関係式】より

…原子力エネルギーは原子核の質量の1000分の1程度をエネルギーに変えて利用する。相対性理論【藤井 保憲】(2)ブラウン運動の理論において導いた関係式。例えば流体中のコロイド粒子などは不規則なブラウン運動を行い，しだいに位置を変えていく。…

【ウィーナー過程】より

…初め，イギリスの植物学者R.ブラウンが顕微鏡で水中にある花粉から出る微粒子を観測しているうちに，それらが激しい不規則運動をしていることを発見した。この運動は，後に水の分子が微粒子と無数といってよいほど頻繁に衝突することによって起こるものであることがわかり，ブラウン運動Brownian movementと呼ばれるようになった。A.アインシュタインは，1905年にこの運動の数学的記述を与え，一定時間内の変移はガウス分布に従うことを理論的に示した。…

【拡散】より

…この消え残った力は絶えずゆらいでいる。これによりコロイド粒子のブラウン運動が見られるのであるが，この運動は決定論によっては決められず，確率法則に支配されている。ここで，ある位置から出発したコロイド粒子が，時間が経つにつれ，空間の中でどんな確率分布をとっていくかを記述するのがスモルコフスキー方程式である。…

【拡散過程】より

…これを放置しておくと粒子は不規則に動きながらも，傾向としては濃度の高いほうから低いほうへ向かって広がり，ついには水全体に一様に分布するに至る。ブラウン運動はこのような現象をモデルとする拡散過程のもっとも重要な例である。一般に，ある区間の中で行動している一次元拡散過程が時間的に一様，すなわち推移確率が時間の差だけに依存するとき，その区間から外に出るまでの行動は，ブラウン運動から状態空間であるその区間の位相的変換と時間変更および粒子を消滅させる方法とで構成される。…

【確率過程】より

…その確率法則は，平均値m(t)＝E｛X_t(ω)｝と共分散関数ρ(t,s)＝E｛(X_t(ω)－m(t))(X_s(ω)－m(s))｝とで決まる。m(t)＝0,ρ(t,s)＝min｛t,s｝(＝tとsの小さいほう)であるガウス過程｛X_t(ω)(t≧0)｝で見本関数が連続であるものをウィーナー過程，またはブラウン運動という。これはR.ブラウンが観察した花粉の微粒子の不規則運動や，A.アインシュタインが研究した分子運動の模型を，N.ウィーナーが数学的に厳密にしたもので，ウィーナーやP.レビの詳しい研究がある。…

【ブラウン】より

…ムラサキツユクサの細胞で複雑なタイプの原形質流動を観察し，原形質流動への関心を高めた。ブラウン運動も彼の発見になる。【佐藤 七郎】。…

※「ブラウン運動」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」