ローレンツ変換（読み）ローレンツヘンカン

デジタル大辞泉

ローレンツ‐へんかん〔‐ヘンクワン〕【ローレンツ変換】

光速度に近い速さで動く物体の運動を二つの慣性系から記述するときの、二つの慣性系間の座標変換。相対運動の速さが光速度よりもきわめて小さければ、ガリレイ変換に一致する。1904年ローレンツが見出し、特殊相対性理論においても確認された。

出典　小学館

精選版 日本国語大辞典

ローレンツ‐へんかん‥ヘンクヮン【ローレンツ変換】

1. 〘 名詞 〙 特殊相対性理論において、互いに一定の速度で動いている座標系の間で、自然法則の形を変えない（光速度の値は一定になる）ように、空間座標と時間座標の関係を与える変換。相対速度が光速度に比べて無視できるときはガリレイ変換に帰着する。一九〇四年、Ｈ=Ａ=ローレンツにより見いだされた。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

ローレンツ変換
ろーれんつへんかん

相対性理論における時間・空間の座標変換。ニュートン力学の法則は、互いに等速運動している座標系を用いても同じ形で与えられる。これはガリレイの相対性原理として知られていたが、1864年に定式化されたマクスウェルの電磁気学、および、その応用としての光の電磁波論の法則は、ガリレイの相対性原理を満足していなかった。このことから、光の波の振動媒質としてのエーテルの静止系が存在するかもしれないと一時期考えられていたが、1905年、アインシュタインが、ガリレイの相対論とは別の相対論が成立することを発見し、電磁気学を含むすべての法則についても、等速運動座標系間において相対性原理が成立していることが確認された。このアインシュタインの相対論における新しい時間・空間の座標の変換式がローレンツ変換である。この変換式は、1892年、H・A・ローレンツにより、電磁気学の法則を不変とする座標変換としてみいだされたものであるが、その同じ変換式を、アインシュタインは、光速度一定の原理と相対性原理を基礎に再発見した。これにより、ローレンツ変換は電磁気学に特有のものでなく、すべての法則の基礎である時間・空間に固有の性質であることが認識された。さらに1908年、ミンコフスキーは、この変換を時間・空間を含む四次元空間における回転に関する対称性として認識した。この対称性はすべての物質の存在形態を決定してもいるのである。

［佐藤文隆］

『アルバート・アインシュタイン著、金子務訳『特殊および一般相対性理論について』（1991・白揚社）』▽『馬場駿羣著『ローレンツ変換の新解釈――時計の遅れや双子のパラドックスの問題も解消しうる』（1991・科学同人研究会）』▽『砂川重信著『相対性理論の考え方』（1993・岩波書店）』▽『松田卓也・二間瀬敏史著『なっとくする相対性理論』（1996・講談社）』▽『菅野礼司著『微分形式による特殊相対論』（1996・丸善）』▽『小玉英雄著『相対性理論』（1997・培風館）』▽『戸田盛和著『相対性理論30講』（1997・朝倉書店）』

[参照項目] | アインシュタイン | エーテル | 光速度 | 時空 | 相対性理論 | 対称性 | 電磁気学 | 等速運動 | 光 | ミンコフスキー | ローレンツ

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

ローレンツ変換 (ローレンツへんかん)
Lorentz transformation

特殊相対性理論において用いられる慣性座標系（慣性系）の間の座標変換。ニュートン力学では，慣性系の間の変換はガリレイ変換で与えられるが，特殊相対性理論ではローレンツ変換がこれに代わる。一つの慣性系S（x，y，z，t）から，x軸方向に速度vで動くもう一つの慣性系S′（x′，y′，z′，t′）への座標変換は，光速度をcとして，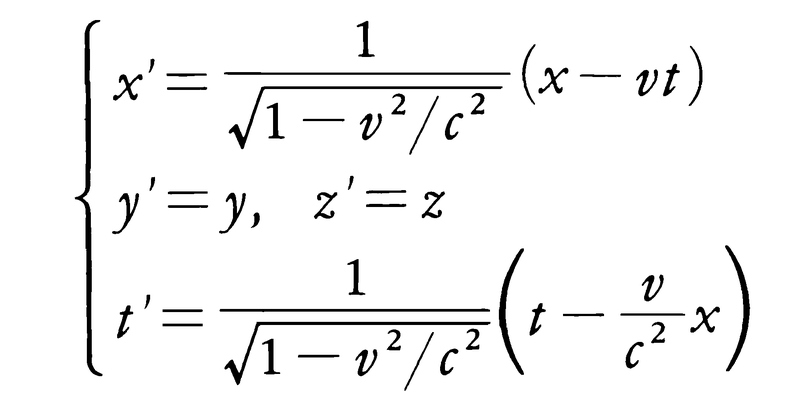

で与えられる。これをローレンツ変換といい，注目すべきは，時間もtからt′へ変換され，とくに時間と空間座標の間に移り変りが起こることである。時間は，もはや空間座標と独立なものではなく，時間と空間を統合した時空という概念に達しなければならない。上記の式そのものは，光速度が方向によって変わらないことを示したマイケルソン=モーリーの実験に関連してH.A.ローレンツがすでに導いていたので，現在でもローレンツ変換と呼ばれているが，アインシュタインはローレンツとは異なるまったく新しい解釈を与えたのである。
→相対性理論
執筆者：藤井 保憲

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

ローレンツ変換【ローレンツへんかん】

特殊相対性理論において用いられる慣性系の間の座標変換。座標系（x，y，z，t）に対して座標系（x′，y′，z′，t′）の軸がたがいに平行であるようにとり，x軸方向に速度vで運動しているとき，ローレンツ変換は（式１）の形になる。この変換は座標系（空間座標x，y，z，時間座標t）の変換のうちx²＋y²＋z²−c²t²（cは真空中の光速度）を不変に保つ。ローレンツがこの変換に対し電磁気学のマクスウェルの方程式が同じ形式を保つことを示したので，この名で呼ばれる。特殊相対性理論では二つの慣性座標系はローレンツ変換で結びつけられ，その諸法則はこの変換に対し形が変わらない。

出典　株式会社平凡社

法則の辞典

ローレンツ変換【Lorentz's transformation】

互いに等速運動を行う二つの慣性系の間の座標と時間の特殊相対論的変換．ある出来事が一方の系で x，y，z，t で起こり，他方の系では x′，y′，z′，t′ であったとすれば

x²＋y²＋z²－t²＝x′²＋y′²＋z′²－t′²

を満たす変換をローレンツ変換という．ただし両座標系の原点が一致したときに t＝t′＝0とおく．変換は4行4列の行列の形で表せる．

出典　朝倉書店

ブリタニカ国際大百科事典 小項目事典

ローレンツ変換
ローレンツへんかん
Lorentz transformation

A.アインシュタインの特殊相対性理論における2つの慣性系間の座標変換。力が働かない物体が等速度運動するようにみえる座標系を慣性系と呼ぶ。1つの慣性系 Sに対して等速度運動している座標系 S′も慣性系である。慣性系 Sおよび S′の空間座標 x，y，z，および x'，y'，z' の座標軸がそれぞれ平行で，S′は Sの x軸の正の方向に速度 vで運動しているとし，時刻 t＝t'＝0 で両座標系の原点が一致していたとすると，ローレンツ変換は，次の式で与えられる。
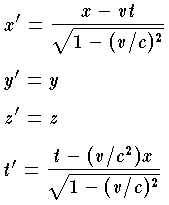なお，cは真空中の光速度を表わすものとする。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のローレンツ変換の言及

【相対性理論】より

…　正しい座標変換としてアインシュタインが(1)式に代わるものとして提出したのは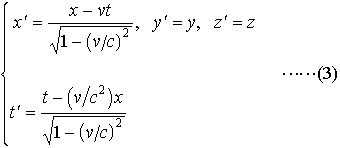，である。この変換式はローレンツ変換と呼ばれ，ローレンツがローレンツ収縮を導いた際に用いたものと同じ形であるが，その前提はまったく異なる(この式の導き方についてはコラム〈ローレンツ変換の導き方〉を参照)。　この変換式が示すもっとも著しい特徴は，空間と時間(xとt)とが互いに移り変わることである。…

※「ローレンツ変換」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」