乗数理論（読み）じょうすうりろん（英語表記）theory of multiplier

精選版 日本国語大辞典

じょうすう‐りろん【乗数理論】

1. 〘 名詞 〙 ある経済変量（独立変数）の他の経済変量への効果を波及効果まで含めて最終的にどの程度の総効果が得られるか、また、その過程はどうかを分析する理論。最終的な総効果を乗数効果といい、独立変数の変化に対し、その変数を含む他の変数の変化がどの程度の割合かを示すものを乗数と呼ぶ。ケインズは特に投資乗数に着目し、その理論の骨子とした。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

乗数理論 (じょうすうりろん)
theory of multiplier

1930年以降に展開されたケインズ経済学の中核をなす理論の一つ。とりあげている問題は，独立支出（とくに投資）の増加が，国民所得の均衡水準をどれだけ上昇させるかという点である。結論を先に述べれば次のようになる。（1）独立支出は所得水準の大きさやその変化に依存しない支出であるが（その代表的なものとして公共投資のための支出などがあげられる），その水準の増加はなされた独立支出と同額ではなく，その〈数倍〉の所得の増加をもたらすということ。そして（2）国民経済における限界消費性向が高ければ高いほど，その〈数倍〉分は大きくなるということ，の2点に要約できる。この〈数倍〉が乗数multiplierと呼ばれる数で，消費と所得との関係によって規定されるものである。

理論の基本的意味

この理論の重要性は，均衡においては所得と総需要は等しいはずであるから，たとえば1億円の独立支出の増加は，均衡国民所得も1億円増加させるはずであるという〈常識〉を打ち破っている点にある。その理由を簡単な数値例を用いて説明しよう。

　いま仮に1億円の独立支出の増加があり，これに見合うだけの所得（すなわち生産物）の増加が発生したとする。ところがこの所得の上昇は次に消費支出をも増加させるため，さらに支出の増加を誘発することになる。はじめの1億円の所得の増加のうち，どれくらいの消費支出が誘発されるのだろうか。これを決めるのが〈限界消費性向〉と呼ばれるもので，追加的な所得の増分のうち，どれくらいの割合がさらに消費されるのかを示す数値（c）である。この誘発された支出に見合うように生産も増加したとすると，所得（生産物）の増加は1億円に加うるにc億円，すなわち（1＋c）億円ということになる。ところがこのプロセスは1度だけで停止するわけではない。（1＋c）億円の所得の増加はさらに消費支出を増加し，その後も同じような循環過程がつづくからである。需要（支出）の増大を満たすための産出量の増大が，さらに需要を増大させる。この循環にはどのようにして終止符がうたれるのだろうか。この問題に答えるためには，無限級数の初歩的な知識が必要となる。

　⊿A円の独立支出（需要）の増大が，同額の生産の拡大を可能にしたとしよう。この⊿A円の生産の拡大は，同額の所得の増加となって，だれかの手中に入るはずである。いま所得（Y）と消費（c）の間に，c＝c＋cYという関係（これは消費関数と呼ばれている）があったとすると，⊿Aの所得の増加はc（⊿A）だけの消費支出の増加を誘発することになる。そして次にこの消費支出の増加を満たすために，c（⊿A）の生産の拡大が必要となり，その結果所得もc（⊿A）だけ増加する。c（⊿A）の所得の増加が，消費関数からc（c⊿A）の量の消費の増加をさらに生み出すことは先に述べた事情とまったく同じである。このようなプロセスによって生まれる消費の増大と，最初の独立支出（⊿A）を合計したものは，

　⊿A＝⊿A＋c（⊿A）＋c²⊿A＋c³⊿A＋……

　　＝⊿A（1＋c＋c²＋c³＋……）

と級数的に表現できる。ここで注意を要することは，限界消費性向を表すcが通常1より小さいため，この幾何級数は収束するという点である。したがって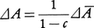，と書き直すことができる。この式は総支出の累積的総計が，最初の独立支出の増加の1/（1－c）倍であることを示している。この1/（1－c）が乗数と呼ばれるもので，cが0と1の間の数であるため，通常乗数は1より大きい。

　以上述べたように，独立支出の最初の増加が，均衡の所得水準（生産物のレベル）を1/（1－c）倍も上昇させる，という点が乗数理論の骨子といえる。乗数は，限界消費性向が高いほど大きくなることはその定義より明らかである。これは限界消費性向が高いと，追加的な所得のうちの大きな割合が消費され，大きな消費支出は，大きな量の生産と所得を誘発するからである。

乗数という言葉の使われ方

ケインズに先だって1931年に，ケンブリッジ大学のR.F.カーンが雇用乗数理論としてこのアイデアの基本部分を展開している。カーンの関心は，消費性向は一定として，公共投資の量を変化させたとき，雇用量がどのような定量的な変化を示すかというところにあった。したがって彼の雇用乗数は，投資財産業における一次的雇用が，限界的に1単位だけ増加したときに，全雇用量が限界的にどれくらい変化するかを示すものである。

　カーンの理論にしろ，ケインズの理論（投資乗数investment multiplier理論）にしろ，公共投資の増加がどのような効果を均衡所得水準や雇用量に与えるのかという点を問題としている。しかしこの理論を実際に使おうとする場合，次の2点に留意しなければならない。一つは，この公共事業の効果を打ち消してしまうような民間投資の減少が起こっていないかということ。もう一つは，限界消費性向が所得や雇用のレベルによって変化しないかということである。とくに前者は，公共投資のための資金需要の増大や物価上昇によって，利子率が上昇し，民間の投資活動が低調になる可能性を示唆している。これはクラウディング・アウトと呼ばれる現象である。

　また外国貿易が存在する場合には，独立支出の増加による乗数効果の一部は，外国における所得と雇用の増加となってあらわれる。これは貿易乗数foreign trade multiplierと呼ばれるもので，輸入品への需要の分だけ，乗数効果が外国へ漏出してしまうからである。この理論はR.ハロッドによってはじめてとりあげられた。

　このように基本的には乗数ということばは，独立支出の変化が均衡産出量に及ぼす変化を論じる際の概念として使われている。しかし最近，時として，より広い意味で，外生変数（その理論によっては説明されない変数）の1単位当りの変化が，内生変数（その理論によって決定される変数）に及ぼす効果（たとえば所得税率の変化が失業率に与える効果），という意味でも使われるようになってきていることを注意しておきたい。
執筆者：猪木 武徳

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

乗数理論
じょうすうりろん
theory of multiplier

ある一定量の投資の増加がどれくらいの所得の増加をもたらすかを明らかにする理論。国民所得決定理論における重要な理論であり、ケインズ経済学の中核をなす理論の一つである。

　国民所得決定理論では、所得Yは、
　　Y＝C＋I
を満たすように決定される。ここでCは消費支出、Iは投資支出であり、また政府部門と外国部門は考慮していない。消費関数は
　　C＝cY＋b c, b＞0
と、所得の一次式で示されるとする。正の定数cは限界消費性向であり、その値は1より小さい。投資は所得に依存しない一定値であるとする。乗数理論は、このように外生的に決定される投資が増えると、それに応じて所得がどれほど増えるかを明確にするものである。たとえば投資がI₀からI₁へと増加したとする。投資がI₀であるときの均衡点は、図ではE₀と示されており、所得はY₀に決定される。投資がI₁へと増えたとする。新しい均衡点は点E₁になり、所得はY₁の大きさに決定される。つまり、投資がΔI＝I₁－I₀だけ増えた結果、所得はΔY＝Y₁－Y₀だけ増えたのである。この所得の増加分の投資の増加分に対する比率、つまりΔY/ΔIの値を乗数という。この乗数の大きさを求めてみよう。図の三角形E₀E₁Aは45度の三角定規の形をしている。したがって辺E₀Aと辺E₁Aの長さは等しくなる。辺E₀Aは所得の増加ΔYを示す。辺E₁Bは投資の増加ΔIに等しい。三角形E₀ABに注意すると、角BE₀Aの角度は限界消費性向cに等しいので、結局、辺BAの長さはcΔYになる。したがってE₀A＝E₁Aより、
　　ΔY＝cΔY＋ΔI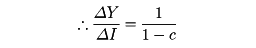

を示すことができる。つまり乗数の大きさは、1から限界消費性向を差し引いて残る値の逆数となる。1から限界消費性向を差し引いた値は限界貯蓄性向とよばれるので、乗数の大きさは限界貯蓄性向の逆数に等しくなる。限界消費性向と限界貯蓄性向の値はそれぞれ1より小さいので、乗数の値は1より大きくなる。つまり投資が増える以上に所得は増えるのである。また人々の消費意欲（貯蓄意欲）が増して（減じて）限界消費性向（限界貯蓄性向）の値が大きく（小さく）なれば、乗数の値は大きくなる。たとえば限界消費性向が0.75から0.8になると、乗数は4から5へと増える。したがってこのような状態では、投資の増加はより大きな所得の増加をもたらす。つまり消費意欲の増大は善、貯蓄意欲の増大は悪となるわけである。ケインズ以前では、貯蓄意欲の増大、つまり倹約は美徳と信じられていたが、ケインズは消費こそは美徳であると主張したのである。このような考え方は「倹約のパラドックス」とよばれる。乗数の値を正確に推定することは、政府が実行する総需要管理政策の有効性にとってたいせつなこととなる。政府支出のうち公共投資を増加させる政策がとられるときに、乗数の値いかんにより、公共投資により誘発される所得の増え方が異なってくるからである。

　これまでみてきたのは投資乗数についてであるが、このほかにもいろいろな乗数がある。たとえば、政府支出の増加がどれくらいの所得の増加をもたらすかを示すのが政府支出乗数であり、輸出の増加はどれくらいの所得の増加をもたらすかをみるのが輸出乗数である。

　また乗数理論は、景気循環を説明するために、加速度原理と組み合わせて用いられている。

［内島敏之］

[参照項目] | ケインズ | 国民所得

乗数理論説明図〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

乗数理論【じょうすうりろん】

投資の増加が国民所得を結局どれだけ増加させるかに関する経済理論。1930年代以後ケインズ経済学とともに発展した。国民所得（支出国民所得）は消費と投資からなるが，たとえば所得の増分のうち消費支出される割合（限界消費性向）が８割であるとすると，投資が増加するとその分だけ国民所得がふえるだけでなく，その国民所得の増分の８割が消費支出され再び国民所得をふやす。さらに，消費支出による所得の増分（最初の投資の８割）の８割は消費支出されてその分だけ所得をふやす（最初の投資の0.8×0.8＝0.64）。この過程はつづいて，結局所得の増大は，最初の投資の増分の〔1/（１−0.8）＝５〕倍になる。この場合の５を乗数という。この投資乗数のほか雇用乗数，貿易乗数などもある。乗数理論は，公共投資による有効需要拡大政策などの手段とされる。
→関連項目貯蓄投資の所得決定理論

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

乗数理論
じょうすうりろん
theory of multiplier

一定期間のマクロ変数の増加分が，どれだけの国民所得増加を生み出すかという経済理論。乗数とは一つのマクロ変数の変化がその変数を成分とする他のマクロ変数に及ぼす限界的な効果をさす。最初に乗数理論を確立したのは R.F.カーンである。彼は第1次雇用の変化が総雇用に及ぼす効果を分析し，第1次雇用に対する総雇用の比率を雇用乗数と呼んだ。これは J.M.ケインズにより，『雇用・利子および貨幣の一般理論』において投資乗数の理論として大成された。乗数理論は相互依存的な経済体系のなかで生じた一つの変化の直接，間接の効果を分析する有用な道具であり，ケインズ以後多くの学者により拡充発展が加えられた。そのほか W.W.レオンティエフ体系を基とする多部門乗数，エコノメトリック・モデルを用いた動的乗数などの研究が行われている。

出典　ブリタニカ国際大百科事典 小項目事典

知恵蔵

乗数理論

経済全体の投資需要が1兆円増えたとすると、この1兆円はどこかの企業に対する需要となり、さらに最終的にはその企業の社員たちの所得になる。その企業の社員たちが、この新たな所得1兆円のうち一定割合、例えばc(0〈c〈1)の割合だけを消費するとすると、このc兆円はまた別の企業に対する需要となり、さらに最終的にはこの別の企業の社員たちの所得になる。このプロセスは無限に続くから、最終的に当初の1兆円の需要増は、1+c+c^2+c^3+…=1/(1‐c)となるが、1‐cは1より小さいので、結局もとの1兆円の需要増の数倍の需要が最終的に経済内に作り出されることになる。例えば、消費性向cが0.8であったとすれば、1/(1‐c)は5になるため、1兆円の当初の需要増は最終的に経済内に5兆円の需要を作り出すことになる。このプロセスのことを乗数効果といい、この理論のことを乗数理論という。

(荒川章義 九州大学助教授 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」

世界大百科事典（旧版）内の乗数理論の言及

【雇用･利子および貨幣の一般理論】より

…31年，ケインズの小冊子〈ロイド･ジョージはそれをなしうるか〉に触発され，R.F.カーンは，政府が公共投資を行って一定数の人を雇用すると，その人の収入が支出され，それが生産を高めて，さらに雇用を増大するというようにして，政府が最初に雇用した数倍の雇用が生ずるという〈乗数の理論〉を展開した。この乗数理論は失業対策としての公共投資に理論的根拠を与えることになった。同時に，これはまた《貨幣論》(1933)の出版後，同書に対して加えられた批判に答える必要を感じていたケインズに新著を書く契機を提供することになった。…

※「乗数理論」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」