展開図（読み）テンカイズ

デジタル大辞泉

てんかい‐ず〔‐ヅ〕【展開図】

立体を平面上に展開させてできる図。多面体では多角形のつながりとして表される。
[類語]見取り図・投影図・透視図・平面図・断面図・立面図・鳥瞰図

出典　小学館

精選版 日本国語大辞典

てんかい‐ず‥ヅ【展開図】

1. 〘 名詞 〙 立体の表面を適当に切り開いて平面上に広げたときにできる図形。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

展開図
てんかいず

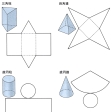
立体の面をその面の量（長さ・角度など）を変えずに平面上に移すこと（合同変換）を展開といい、その移された平面図形を展開図という。面が平面である多面体の場合には完全な展開図が得られるが、曲面の場合はかならずしもそうではない。完全な展開図の可能な面を可展面という。それは直線（母線）の移動によってできる曲面である線織面のなかでも限られたもので、単曲面が該当する。円柱・円錐(えんすい)・類似螺旋(らせん)面（螺線の接線により構成される面）などがその代表例である。曲面では、可展面といっても、原理的に可能だということであって、展開法は近似法によって求めるのが普通である。

　多面体の展開図は多角形のつながりとして表される。直円柱の展開図は側面からできる長方形と二つの底面の円からできている。また、直円錐の展開図は側面からできる扇形と底面の円からできている。

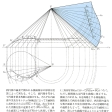
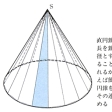
　たとえば、斜円錐では、底円の円周を等分し、その等分点と斜円錐の頂点をおのおの頂点とする多角錐を仮定する。多角錐の展開は、稜(りょう)の実長、面の実形が求めやすいので、容易である。その際、等分点の数を増せば、多角錐は円錐に近似しうるので、より近似した展開図が得られる。これは展開図の形から放射線法といわれる。

　このように円錐は、円柱と同様、展開図が得られやすいので、可展面でない曲面をその部分ごとにこれらで近似させ、それをさらに多面体で近似展開する方法がある。しかし、一般的には、曲面上の点を結んでできる小三角形よりなる多面体に近似する方法がとられる。三角形法という。

　展開図の作成目的は種々（たとえば建築での室内展開図など）あるが、そのなかで重要なものとして測地線の問題がある。測地線とは、面上の2点間の最短距離を示す線であるが、その面の展開図上では、その線は直線となる。したがって、2点の展開図上の位置を求め、それを直線で結び、展開図を元の面に戻す際にこの直線上の各点を面上に移すことで、測地線が求められる。

［玉腰芳夫］

展開図

展開図（正多面体）

斜円錐の展開と測地線

円錐の近似法

単双曲線回転面の近似展開（三角形法）

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

展開図 (てんかいず)
development

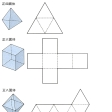
空間にある立体に適当な切れめを入れて，それを1平面上に広げることをその立体を平面上に展開するといい，このとき平面に現れる図をその立体の展開図という。例えば，直円錐と正十二面体の展開図は図1，2のようになる。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

展開図【てんかいず】

立体を展開して描いた図形で，立体各面の実形の連続である。展開の不可能な立体は錐面などに置き換えて近似的な展開を行う。板金工作などでは，物の実形より展開図のほうが広く使用されている。

出典　株式会社平凡社

世界大百科事典（旧版）内の展開図の言及

【製図】より

…(5)回転投影図　ボスからある角度で腕が出ているような品物の場合には，その部分を一直線上まで回転して，その実形を図示するのがよい(図3-d)。(6)展開図　板を曲げてつくるような品物の場合には，曲げ加工を行う前の形状を展開図として図示しておくのがよい。(7)対称図形の省略　対称形状の品物の場合には，省力化のために対称中心線の片側の図形だけをかくことができる。…

※「展開図」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」