透視図（読み）トウシズ

デジタル大辞泉

とうし‐ず〔‐ヅ〕【透視図】

透視図法1によって描いた図。
[類語]見取り図・展開図・投影図・平面図・断面図・立面図・鳥瞰図

出典　小学館

精選版 日本国語大辞典

とうし‐ず‥ヅ【透視図】

1. 〘 名詞 〙 ある視点から見た物体の形を平面上に書き表わした図。
   1. [初出の実例]「暗い建築の陰影、裸の並木、疎らな街燈の透視図」(出典：冬の日（1927）〈梶井基次郎〉二)

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

透視図
とうしず

できる限り目に見える形に近い図を平面上に描こうとして生まれた、幾何学的図法による図である。中心投影図の一類。

　古代ギリシアの絵画やレリーフにすでにその萌芽(ほうが)がみられるが、図法自体への着目はイタリア・ルネサンスのF・ブルネレスキやL・B・アルベルティを待たねばならない。この図法の発展途上で注目されるのは、G・デザルグで、透視図と元の図形の間にある幾何学的関係についての「デザルグの定理」は、のちに生まれた射影幾何学の基本定理となった。

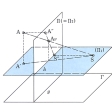
　透視図の基本は、目（視点）と元の図形の諸点を結ぶ直線（視線）を考え、それと平面（画面）との交点が元の諸点の透視図であるとするものである。その際これらの基盤となる平面（基面）を考え、基面に垂直な画面を直立画面、そうでないのを傾斜画面という。後者は比較的大きな対象、もしくは近くから描く場合、前者に生ずる好ましくないゆがみを避けるために用いられ、鳥瞰透視図(ちょうかんとうしず)（俯瞰(ふかん)透視図）と仰瞰透視図がある。

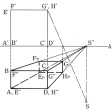
　視点を含み、基面に平行な平面と画面との交線を地平線という。直立画面の場合、この平面を正投影の水平投影面、画面を直立投影面とみなして、元の諸点、視点、視線の平面図と立面図を図示し、それによって視線と画面との交点、すなわち透視図を求めうる。直接法といって、透視図法の基本である。

　直線の透視図は、直線上の2点の透視図を結ぶことで求めうる。この透視図上の点ではあるが、元の直線に平行な視線と画面との交点は、平行線は交わらないという公理によれば、元の直線上の無限遠の点という実在しない点に対応することになり、もはや透視図ではない。つまり、透視図上でその点だけ消えているという意味で、それを消点という。互いに平行な直線の消点は同一であるので、それらの透視図はこの消点に集まる直線である。この性質を用いる画法を消点法という。また直線と画面との交点（始点）はそれ自体透視図でもある。始点から消点までの透視図を全透視という。

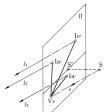
　傾斜画面によって直方体の透視図を求めようとすると、各稜(りょう)に平行な視線は三主方向の直線となり、消点は通常三つとなる。この三消点は図に潜む直角三角形に着目することで求めうる。これを三消点法という。一般の立体の場合のその透視図は、直方体を基礎にして構成、作図するのが通常である。

［玉腰芳夫］

『日本図学会編『図形科学ハンドブック』（1980・森北出版）』

[参照項目] | デザルグの定理 | 投影図

透視図（直接法）

透視図（直線lの消点）

透視図（平行線の消点と全透視）

透視図（消点法）

透視図（測点法）

透視図（三消点法）

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

透視図 (とうしず)
perspective projection

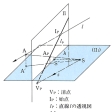
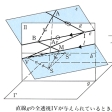
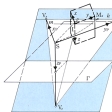
Fを空間図形とし，Sは空間内の1点，αはSを含まない1平面とする。このとき，Fの点Pに対し，SとPを結ぶ直線がαと交わる点をP′とすれば，PがF上のすべての点を動くとき，P′はα上に一つの図形F′を描く（図）。F′をFの透視図または中心投影図といい，Sを視点または光点，αを透視面または画面，直線SPを視線という。透視図では原図形における長さや角などは保たれないでゆがんでしまうが，それでもある種の幾何学的性質が保たれている。例えば，点は点に，直線は直線にうつり，〈いくつかの点が共通の1直線上にある〉とか〈いくつかの直線が共通の1点で交わっている〉といった性質は保たれている。透視図は空間図形を平面上に表す一つの方法として用いられる。
→画法幾何学
執筆者：中岡 稔

図－透視図

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

透視図【とうしず】

有限の距離にある一つの視点と，物体各点とを結びつける放射線によって描き表した図。遠近法に従って，視点に近い部分ほど大きく，遠い部分ほど小さく表され，物体を実際に見たときの感じに描かれる。

出典　株式会社平凡社

世界大百科事典（旧版）内の透視図の言及

【遠近法】より

…中世ヨーロッパでは光学と同義に用いられた。狭義には線的遠近法あるいは透視図法と訳されるが(透視図)，広義には絵画･浮彫などの二次元的造形表現における空間知覚の表現方法のすべてに適用される。自然主義的な絵画や浮彫は，三次元的な空間と個体およびそれら相互の関係から成り立つ現実を二次元に表現しようとするものであるから，多少なりとも現実的世界に似た表現を企てる芸術作品は，すべてその固有の遠近法をもっていると考えることができる。…

※「透視図」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」