熱力学の法則（読み）ネツリキガクノホウソク（英語表記）laws of thermodynamics

デジタル大辞泉

ねつりきがく‐の‐ほうそく〔‐ハフソク〕【熱力学の法則】

熱力学の基礎をなす三法則。（1）第一法則。物体に外部から加わった仕事と熱量との和は、内部エネルギーの増加に等しいという法則。熱と仕事は等価で、熱を含めてエネルギーは保存される。（2）第二法則。熱は高温から低温に移動し、その逆は起こらないという法則。あるいは、孤立系のエントロピーは不可逆変化によって増大するという法則（エントロピー増大の法則）。（3）第三法則。絶対零度ではどんな物質のエントロピーも零になるという法則。
[補説]これら三法則に加え、物体AとBが熱平衡にあり、物体BとCも熱平衡な場合、AとCは必ず熱平衡の状態であるという熱力学第ゼロ法則が定義される。

出典　小学館

精選版 日本国語大辞典

ねつりきがく【熱力学】 の 法則(ほうそく)

1. 熱力学の基礎となっている根本法則。第一法則は、熱はエネルギーの一形態であるという考えに立ち、エネルギー保存の法則を熱現象にまで広げたもの。第二法則は、高温から低温への熱の移動は不可逆で、その逆の変化を起こすためには外からエネルギーを与えなければならないということ。熱現象の不可逆性。第三法則は、絶対温度が零度の極限で、どんな物質のエントロピーも零になるということ。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

熱力学の法則 (ねつりきがくのほうそく)
laws of thermodynamics

熱が関係するさまざまな現象を取り扱う普遍的な理論体系である熱力学は，熱平衡状態と経験的温度に関する第0法則，エネルギー保存則である第1法則，熱現象の不可逆性についての第2法則，そして絶対0度における状態に関する第3法則を基本法則とする。これらの四つの法則を総称して熱力学の法則という。熱の本性は物体を構成する電子や原子核のような微視的な粒子の運動に求められるが，熱力学の法則は巨視的なレベルでの熱現象に関して，物体の微視的構造にかかわりなく厳密にしかも一般的に成立する法則である。

熱力学の第0法則

外界から孤立させて物体を放置しておくと，もはや何の変化も生じない状態になる。この状態を熱平衡状態という。二つの物体を接触させると最初は一方から他方へ熱の移動が生ずるが，長時間たつとやはり何の変化も起こらなくなる。このとき二つの物体は互いに熱平衡にあるという。熱平衡にある二つの物体の間では熱のやりとりがちょうど打ち消しあう。熱平衡に関して，〈物体AとBとが熱平衡にあり，BとCとが熱平衡にあるならば，AとCも熱平衡にある〉という法則が成り立つ。この法則は熱力学の体系がつくられたあとでJ.C.マクスウェルが基本法則の一つに数えたため，第0法則と呼ばれるようになった。

　第0法則のおかげで経験的温度を考える，いいかえると温度計を使うことが可能となる。すなわち，物体Bを物体Aと熱平衡の状態にしたあと，物体Cと接触させたときBに何の変化も認められない場合，AとCとは同じ温度にあるという。このときBが温度計の役割をするわけであり，変化のあるなしは例えば水銀柱の高さで見るのである。

熱力学の第1法則

物理学のもっとも基本的な法則の一つは，どんな物理的変化においてもそれに関係するすべての物体のもつエネルギーの和は不変であるというエネルギー保存の法則である。熱力学の第1法則はこのエネルギー保存則にほかならないが，とくに熱がエネルギー変化の一形態であることを明らかにして，ふつう次のように述べられる。〈物体をある定まった状態から他の定まった状態に移すために，外界から物体に与えなければならない熱量Qと仕事量Wとの和Q＋Wは，どんな方法によっても一定である〉。すなわち，状態aからbへの変化に要する全エネルギーQ＋Wは，初めと終りの状態a，bだけによって定まり，その過程にはよらない。ここで力学的エネルギー，電磁気的エネルギー，化学的エネルギーなどを総称して仕事と呼ぶ。また物体が外界に熱や仕事を与える場合にはそれらの量は負の値をとるものとする。かりに第1法則が成り立たないとすると，a→bという状態変化とその逆の変化b→aを異なる過程で生じさせることにより，無からエネルギーをつくり出すことができる。いいかえると無からエネルギーをつくり出す装置，すなわち第1種の永久機関が可能になる。したがって第1法則を，〈第1種の永久機関は不可能である〉と表現してもよい。第1法則は19世紀の半ばころまでに，B.トンプソン（ランフォード），J.P.ジュール，J.R.マイヤー，H.ヘルムホルツらによって確立された。

熱力学の第2法則

力学で扱う運動はすべて可逆，すなわちある運動が可能であればそれを逆向きにたどる運動も可能である。しかし非常に多くの粒子から構成されている巨視的な物体では，変化が一定の方向にだけ進み，その逆の変化は生じない場合が多い。運動は摩擦によって減衰し熱が発生するが，その逆は起こらない。またインキを水の中に落とすと拡散していくが，自然に集まることはない。このような変化のことを不可逆変化と呼ぶ。第2法則は，自然界で生ずる熱現象がどういう方向に進むかを述べたものである。互いに同等な第2法則の表現のしかたがいくつかあるが，ここではそのうちの二つだけをあげておく。一つは，〈熱は高温から低温に移る〉という表現である。すなわち，熱の移動は不可逆であり，低温から高温の物体に熱を移し，それ以外には何の変化も残さないという逆過程は不可能である。これはR.クラウジウスによる表現である。もう一つはW.トムソン（ケルビン）の与えた表現で，〈仕事が熱になる過程は不可逆である〉というものである。したがって，その逆の過程を行う装置，すなわち熱源から熱を取り，それをすべて仕事に変え，それ以外に外部に何の変化も残さずもとの状態に戻る装置，いわゆる第2種の永久機関は不可能である。第2種の永久機関は第1法則には反していないことに注意しなければならない。かりに第2種の永久機関が可能であれば，大気や海水から熱をとり出して電力に変えられるから，なにも石油を燃やしたり核反応を起こしたりして高温をつくらなくても発電できることになる。われわれの経験によると現実にはこのようなことはありえないから，第2法則が普遍的に成り立つことには疑いがない。熱を仕事に変えるには必ず高温の熱源と低温の熱源が必要であり，熱の一部を低温の熱源に捨てなければならない。

　第2法則は一見当然すぎることを述べているように思われるが，第1法則と組み合わせると熱力学の体系がそのうえに展開されるのである。その第1歩は絶対温度およびエントロピーの導入である。エントロピーは内部エネルギーと同様に状態量，すなわち物体の一つの定まった熱平衡状態で定まった値をとる量である。このエントロピーという量を使うと，第2法則は，外界から孤立した物体の系で生ずる変化では系全体のエントロピーは必ず増大するというエントロピー増大の原理として表される。熱平衡状態にある物体に外部の熱源から微小な熱量⊿Qを与えたとき，その物体のエントロピーSは，⊿S＝⊿Q/Tだけ変化する。ここでTは問題にしている状態の絶対温度である。温度T₁，T₂（＜T₁）の二つの物体1，2を接触させ，⊿Qの熱を1から2に移動させると，二つの物体のエントロピーの変化の和は，

　（⊿Q/T₂）－（⊿Q/T₁）＝⊿Q（1/T₂－1/T₁）

に等しい。T₁＞T₂であるからこれは必ず正である。すなわち熱が高温から低温に移るときエントロピーは必ず増大する。

　熱力学の第2法則は，1820年ころ行われたS.カルノーの熱機関に関する先駆的研究をもとに，R.クラウジウス，ケルビンが基本法則として認識した。

熱力学の第3法則

第2法則から定められるのは物体の二つの熱平衡状態におけるエントロピーの値の差である。例えば一定量の気体をある熱平衡状態から温度，圧力の異なる他の状態へ移したとき，どれだけエントロピーが変化するかが定められる。したがって定数だけの任意性が残るわけであり，とくに絶対0度での物体のエントロピーの値が問題になる。第3法則は，一般に物体のもつエントロピーは温度が0Kに近づくと0になることを主張する。W.H.ネルンストは，気体，液体などの熱的性質の詳細な研究から，1906年に発表した論文で，絶対0度に近づくといかなる変化におけるエントロピーの変化も0に等しくなるという定理を提出した。第3法則はこのネルンストの定理をM.プランクが精密化したもので，第3法則そのものをネルンストの定理，またはネルンスト=プランクの定理と呼ぶこともある。

統計力学による基礎づけ

物質の微視的構造に立ち入って電子や原子核の運動から物体の熱的性質を明らかにする統計力学が，熱力学の成立後20世紀になって確立された。熱力学の諸法則も統計力学の立場から基礎づけられる。第1法則はエネルギー保存則であり，微視的なレベルでのいかなる物理的過程でも成立しているから問題はない。第2法則に関しては，L.ボルツマンが，1870年代に行った一連の研究によりエントロピーの統計力学的な意味を明らかにした。内部エネルギー，温度，体積，圧力などで指定される巨視的状態のエントロピーは，その巨視的状態に対応する微視的状態の数Wの対数で与えられるというのである。すなわちエントロピーという量は，微視的に見たときに巨視的状態に存在する無秩序さ，例えば原子の運動，あるいは配列の乱雑さの度合を表す。したがって第2法則は，より無秩序の度合の大きい方向に巨視的な物体の変化が生ずることを意味する。第3法則は，絶対0度になると（つねに熱平衡状態として近づくと），一般に物体の状態は微視的に見ても一つである，いいかえると乱れはなくなることを主張する。例えば常圧下では，ヘリウムを除くすべての物質は0Kで完全な結晶，つまり原子が規則正しく整列した状態になる。一般的には第3法則は量子力学によって初めて基礎づけられた。
→エントロピー　→統計力学　→熱
執筆者：恒藤 敏彦

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

熱力学の法則
ねつりきがくのほうそく

熱力学の原理、つまり基本法則は、まず熱平衡状態の存在を規定する熱力学第ゼロ法則、熱と仕事の関係を与える熱力学第一法則、熱の移動形態を与える熱力学第二法則がある。さらに、量子力学に基づき基底状態のエントロピーがゼロであるとする熱力学第三法則（ネルンストの熱定理）がある。

［宮下精二］

熱力学第一法則

物体の温度を上げるために、高熱源と接することでの熱流入による温度上昇と、仕事によって生じる運動の摩擦による温度上昇の二つの方法があることから、熱の移動はある種のエネルギー移動形態であることが明らかになった。この熱というエネルギー移動形態を含めたエネルギー保存法則を熱力学第一法則という。物体がもつ全エネルギーを内部エネルギーUとし、その変化を、外から加わった仕事d´Wと熱の移動d´Qを用いて
dU＝d´W＋d´Q
と表すことができる。ここで、熱や仕事は状態を与えても一意的に決まらない量であり、数学でいうところの完全微分でないため、その変化量を表すのにダッシュをつけている（d´）。それに対し内部エネルギーは状態によって一意的に決まる量（状態量という）であるので、その変化を表すのにdを用いている。しかし、d´Wは仕事であり、状態量を用いて表すことができる。たとえば、体系の体積をV、その微小変化をdV、また体系に働く圧力をPとすると、熱力学第一法則はd´W＝－PdVとなる。ここで、V,Pは共に状態量である。また、d´Qも熱力学第二法則から導かれる性質を用いると、温度TとエントロピーSを用いてd´Q=TdSと表される。

［宮下精二］

熱力学第二法則

熱の流れは高温部から低温部に向かって不可逆に起きることを表す法則である。この法則はさまざまな形で表現される。たとえば「外部になんら変化を残さずに、熱が低温部から高温部へ移動することはない」（クラウジウスの原理）や「外部になんら変化を残さずに、熱が全部仕事に変わることはない」（トムソンの原理）などである。両者は一見異なっているように思われるが等価であることが証明できる。この原理から、温度Tの定義を導入することができ、さらに熱の移動に関して、熱力学関数としてエントロピーという量Sを定義することができる。これらを用いると可逆過程ではd'Q＝TdSとなる。温度とエントロピーの定義はこの関係を満たす範囲で任意性をもつが、通常、ボイル‐シャルルの法則で用いられる気体温度計の温度を採用する。熱力学第二法則は、任意の状態の変化に伴う熱の移動に対してdS≧d'Q/Tと表すことができる。この法則は時間反転対称性を破るものであり、そのミクロな起源に関して種々の議論がなされている。

［宮下精二］

熱力学の基本方程式

熱力学の第一、第二法則は次の関係
dU＝TdS－PdV＋μdN
にまとめられる。ここで、TdSは熱の移動をエントロピーで表わしたものであり、－PdVは仕事の代表としての圧力による体積変化に伴うエネルギーであり、μdNは粒子数の変化に伴うエネルギー変化を表す項である。ここでμは化学ポテンシャルとよばれる。この関係から偏微分に関する関係を用いることで、すべての熱力学的関係が導かれる。たとえば圧力一定下での比熱（定圧比熱）をC_P、体積一定下での比熱（定積比熱）をC_V、とすれば、偏微分に関する恒等式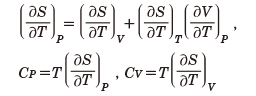

から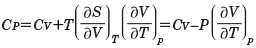

が得られる。この関係は物質によらず一般に成り立つ。たとえば、理想気体の場合、この関係は状態方程式PV＝nRTを代入して利用すると、マイヤーの関係式として知られている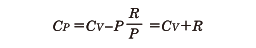

となる。

［宮下精二］

[参照項目] | 永久機関 | エントロピー | 温度 | 化学ポテンシャル | カルノー・サイクル | 基底状態 | 自由エネルギー | 状態方程式 | 熱平衡 | ネルンストの熱定理 | 理想気体

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

熱力学の法則【ねつりきがくのほうそく】

〔第１法則〕　〈物体系が状態AからBへ移るとき，物体に外部からなされた仕事と外から加えられた熱量との和は，状態A，Bだけできまり途中の経路に関係しない〉。これは熱現象に適用されたエネルギー保存の法則。〔第２法則〕　種々の表現があるが内容は同等。〈高温の物体から低温の物体に熱を移し，それ以外には何の変化も残さないという過程は不可逆である〉（クラウジウス）。〈仕事が熱になる過程は不可逆である〉（ケルビン）。これは不可逆変化の存在を主張するもので，数学的にはエントロピーの存在と増大法則で定式化される。〔第３法則〕　ネルンストの熱定理（1906年）とも。〈化学組成の単一な均質物質のエントロピーは，絶対０度に近づくにつれて化学的性質・相・圧力に無関係に０に近づく〉（プランク）。これは〈有限回の操作によって絶対０度の状態に達することは不可能である〉とも表現される。
→関連項目エネルギー｜エントロピー（熱）｜カルノーサイクル｜クラウジウス｜ケルビン｜ジオーク｜絶対零度｜内部エネルギー｜熱｜熱力学

出典　株式会社平凡社