音律（読み）オンリツ

デジタル大辞泉

おん‐りつ【音律】

１ 楽音の調子。また、音楽。
２ 音の高さの相対的な関係を整理した体系。純正調・平均律など。
[類語]調子・音調・調性・音階・音程・音高・トーン・拍子・拍はく・律動・乗り・リズム・テンポ・調べ

出典　小学館

精選版 日本国語大辞典

おん‐りつ【音律】

1. 〘 名詞 〙
2. ① 各種の楽音の調子。音楽の調子。また、音楽。
   1. [初出の実例]「曲(ふし)をただし、音律を習知するは、流躰を作付する也」(出典：曲附次第（1423頃）)
   2. [その他の文献]〔説苑‐脩文〕
3. ② 音楽に使われる音の高さの相対的な関係を、音響学的に位置づけた平均律、純正調などの体系。
4. ③ 中国、日本音楽の十二律で、音の高さのこと。

いん‐りつ【音律】

1. 〘 名詞 〙 音楽の調子。歌舞音曲一般の呼称。
   1. [初出の実例]「音律 インリツ」(出典：文明本節用集（室町中）)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

音律 (おんりつ)

音階を構成する諸音の音高関係を数理的に規定したものを音律と呼び，一定の音律に従って楽器の音を整えることを調律という。中国および日本では，音律に近い概念を表す言葉として楽律が用いられてきた。音律は古来，地域的にも歴史的にも種々のものが考案されてきたが，その中には純理論的・数学的な関心から生まれ，実用に付されなかったものも少なくない。音楽で実用された音律は，理論的整合性と実践的要求との調和を求めて変遷してきたといえる。楽音の絶対的な高さは単位時間（通常は1秒を単位とする）内における振動数によって決まるが，音律はあくまで音の相互関係を問題とするので，振動数の絶対値は重要でなく，音律の表示には振動数の比（音程比），またはその対数値（音程値）が用いられる。純正な音程比は弦長の調和分割によって得られ，最初の弦長を1とすると，それを2等分してオクターブが，オクターブ（1：2）を調和分割して完全5度（2：3）と完全4度（3：4）が，完全5度の調和分割によって長3度（4：5）と短3度（5：6）が，長3度の調和分割によって大全音（8：9）と小全音（9：10）が得られる。オクターブの分割によって得られるこれらの音程比は，自然倍音列内の音程比と一致する。一方，音程値には種々のものが提案されたが，今日最も普及しているのは，12等分平均律の半音を100セント（したがってオクターブは1200セント）とするセント値である。
→音程

西洋

西洋における音律の歴史は，単旋律音楽から声楽ポリフォニーへの発展，鍵盤楽器の台頭，調の拡大など，音楽様式そのものの変化と深くかかわり合っている。

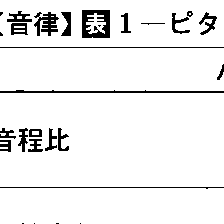
ピタゴラス音律

古代ギリシアでもすでに種々の音律が算定されたが，最も重要なものは，中世まで音律論の基礎となったピタゴラス音律である。この音律は完全5度（3/2）を次々に重ねて新しい音を獲得するので，5度音律ともいわれる。この音律の諸音は数学的にいえば（3/2）ⁿ（n＝0，1，2，3，……）によって与えられる。たとえば出発音をハとすると，そのハは（3/2）⁰＝1，トは（3/2）¹＝3/2，は（3/2）²＝9/4（オクターブ下げると9/4×1/2＝9/8），は（3/2）³＝27/8（オクターブ下げると27/8×1/2＝27/16）等々となる。このようにして得られた諸音を1オクターブ内にまとめると，ハ調長音階の音律は表1のようになる。しかし，（3/2）ⁿ＝（1/2）^mという等式を満足させる整数のn，mは存在しないから，nの値をいくら大きくしても，つまり完全5度を何回重ねても，出発音と同名の音に到達することがない。たとえば，5度を12回重ねた音とオクターブを7回重ねた音は（3/2）¹²：（1/2）⁷＝3¹²：2¹⁹＝531441：524288となり，両音のあいだにはピタゴラス・コンマと呼ばれる微小な差（23.46セント）が生じる。つまり，5度音律においては5度圏が閉じた円環とならず，無限のらせんを形成することになる。具体的には，たとえば音と嬰ロ音が異名同音とならずに，微小な音高差をもつ異名異音となる。ピタゴラス音律の第2の問題点は，表1から明らかなごとく，ハ-ホのような長3度が81/64という複雑な比を成して協和性に乏しいことである。この長3度は全音2個の積重ねとして得られたもので（9/8×9/8＝81/64），特に2全音（ディトヌスditonus）と呼ばれる。

純正律

西洋のポリフォニーにおいて，14世紀までは完全5度と完全4度が和声音程の中心だったが，15世紀に入ると長・短3度の重積による3度和声が主流となり，それとともに，不協和な長3度をもつピタゴラス音律に代わって，純正律が好まれるようになった。純正律とは，自然倍音列に現れる純正5度（3/2）と純正長3度（5/4）の組合せによって，音階中の諸音が単純な整数比となるように定められた音律である。純正5度をQ，純正長3度をTと表せば，純正律音階の諸音はmQ＋nT＝（3/2）^m×（5/4）ⁿという方程式によって与えられる（ここでn＝0とおけばピタゴラス音律となる）。表2は純正律長音階の音程比を示すが，ここで注目すべきことは，ピタゴラス音律とちがって，全音に9/8と10/9の2種類が現れる点である。前者を大全音，後者を小全音と呼び，両者の差（9/8×9/10＝81/80）をシントニック・コンマと称する。

　純正律においては，主要な3和音に関して最もよく協和する純粋な響きが得られるが，全音に大小の2種類があるため，転調や移調には大きな困難が生じる。たとえば，表2の音階をト長調に移すためには，ト-イの関係を10/9ではなく9/8に，イ-ロの関係を9/8でなく10/9に変更しなければならない。無伴奏合唱曲や弦楽合奏の場合にはこのような微細な調整も比較的容易だが，音高が固定している鍵盤楽器においては，基本音階以外の調を演奏するためには鍵の数が著しく増加することとなり，まったく実用に適さない。16世紀から鍵盤音楽が台頭してくると，純正律は理論的研究の対象たるにとどまり，音楽の実践からは姿を消すことになった（ただし今日でも，無伴奏合唱曲や弦楽合奏において，主要な和音の音程を純正にとることはしばしば行われる）。

中全音律

ピタゴラス音階の難点は長3度が純正長3度よりシントニック・コンマだけ広い（81/64×4/5＝81/80）不協和音となること，また純正律の難点は大小2種類の全音をもつことから生じた。中全音律というのは，純正長3度を保ちつつ，なおかつ大全音と小全音の区別を解消した音律である。その全音の幅は大全音（9/8）と小全音（10/9）の真ん中にあるので中全音と呼ばれ，音程比で表せば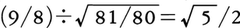となる。中全音律は鍵盤楽器においてすでに15世紀から実用されていたらしいが，理論的に体系化されたのは16世紀後半のことで，その後18世紀中ごろにいたるまで最も一般的な音律となった。これによって，ピタゴラス音律や純正律に比べて多くの調が実用可能となったが，調号の多い調ではきわめて耳ざわりな不協和音の生じるのが欠点である。

12平均律

一般に平均律とは，ピタゴラス音律や純正律で生じる微小な音程差（コンマ）を調整して実用に便利なものとした音律を指す。それは等分平均律と不等分平均律に大別され，そのおのおのについてもさまざまな種類があって，前述の中全音律も不等分平均律の一種にほかならない。しかし今日〈平均律〉といえば，12平均律を指すのが普通である。これはオクターブを12個の半音に等分し（¹²\(\sqrt{2}\)），すべての音程をこの単位音程の倍数として定める。したがってオクターブ以外の音程はすべて複雑な比となって純正音程からずれているが，その反面，24の調をすべて均等に使える点で実用上大きな利点をそなえている。表3はハ調長音階について，ピタゴラス音律，純正律，中全音律，12平均律のちがいをセント値によって示したものである。

　12平均律の理論はすでに16世紀末の中国の朱載堉（しゆさいいく）や17世紀末の日本の中根元圭にも見られ，西洋でも17世紀初頭から多くの例が存在したが，それが実用化されるのは18世紀後半を待たねばならなかった。J.S.バッハの《平均律クラビア曲集》第1巻（1722）は，12平均律を実用化した最初の芸術的成果とされてきたが，今日では，この曲集さえも一種の不等分平均律によっていたとするのが定説となった。しかし18世紀後半以後，西洋音楽は一般に12平均律を基盤として発展し，ロマン派の半音階的和声や遠隔な転調も，シェーンベルクの12音技法も，すべてこの音律のおかげで実現可能となったのである。遺稿《音楽の合理的・社会学的基礎》（1921。邦訳《音楽社会学》）の中で洋の東西について音律の発達を比較研究したM.ウェーバーの言葉を借りるならば，西洋音楽は音律の理論的整合性を犠牲にしながらも，12平均律によっていわば目的合理性を獲得したのであった。
執筆者：角倉 一朗

東洋

音律は古来，音楽の実践上の必要のみならず，知的な，とりわけ数学的な関心から研究がすすめられた。ここでは主としてアジアの歴史的に重要な音律論を二，三挙げる。

　中国ではすでに《呂氏（りよし）春秋》に十二律の概念が現れ，1オクターブ中に12の音律が規定されていた。これは黄鐘（こうしよう）を基準音として三分損益を繰り返し算出して得られる11音を高さの順に並べ変えて，下から黄鐘，大呂（たいりよ），太簇（たいそう）／（たいぞく），夾鐘（きようしよう），姑洗（こせん），仲呂（ちゆうりよ），蕤賓（すいひん），林鐘（りんしよう），夷則（いそく），南呂（なんりよ），無射（むしや）／（ぶえき），応鐘（おうしよう），黄鐘とした。これはピタゴラス音律の算定法と同じ原理に基づくもので，第12番目に得られる1オクターブ上の黄鐘は，厳密にいえば，基準音と同律ではなく，ピタゴラス・コンマだけ高くなってしまう。前漢の京房（きようぼう）は三分損益をさらに反復して60律まで求めた。また宋の銭楽之（せんがくし）（5世紀）はこれをいっそう推し進めて360律まで求め，この不整合を解決しようとしたが，これらは音楽の実践には応用されなかった。古代中国の理論家の精密な音律の追求は，奏楽のためというよりもむしろ思弁的な，宇宙論的な関心の結果である。のちに南宋の蔡元定（12世紀）は独自の考えによる18律をもって（《律呂新書》），また明の朱載堉は12平均律の発見（《律呂精義》1606）によって実用化を試みた。

　インドでは古来1オクターブが22律から成るとする理論が順守されていた。バーラタの《ナーティヤ・シャーストラ》によれば，1オクターブが原則として七つの音階音をもつが，それぞれは2，3，または4律の微小音程（シュルティ）から成り，その配分は不均等である（表4）。すなわち，この2種の音階は第5度（パ音）に異同があり，サ音階では13シュルティの音程をもつが，マ音階では12シュルティでわずかに幅が狭い。ちなみに，13シュルティは702セントで純正律の完全5度に近い。ただし今日のインド音楽の実践は1オクターブを22律とはせず，むしろ12律とするのを原則としており，これはピタゴラス音階とほぼ重なる。

　西アジアでは音律の計算が数学の一分科として，学者の関心を引いていたので，古来，大哲学者といわれる人々は多かれ少なかれ音律に言及している。その中で今日まで原理的に順守されているのは，サフィー・アッディーンの1オクターブ17不等分律音階である。この理論によれば，大全音（204セント）は二つのリンマ（L＝90セント）と一つのコンマ（C＝24セント）から成り，テトラコルド（完全4度）は（L＋L＋C）＋（L＋L＋C）＋Lの7律から構成される。したがって1オクターブは二つのテトラコルドと1大全音，すなわち，（L＋L＋C）＋（L＋L＋C）＋L＋（L＋L＋C）＋（L＋L＋C）＋L＋（L＋L＋C）の17律から成るとする。ここでは西アジアに特有な中立音程（例えば〈ザルザルの中指〉や〈ムジャンナブ〉）がL＋C（＝114セント）とかL＋L（＝180セント）の音律で理論づけられる。しかし19世紀になって西洋の平均律を基礎とし，その半音をさらに2等分にした24等分律がレバノンのムシャーカ（1800-88）によって唱えられ，これが今日の西アジアの音楽の実践面に大きな影響を及ぼしている。
執筆者：柘植 元一

日本

日本においては，中国の楽律理論を移入したものの，実際の音楽に通用する理論としては発展せず，江戸時代の声明（しようみよう）家や漢学者（荻生徂徠，富永仲基など）によって，中国の理論の研究がなされたのみであった。ただ和算家の中根元圭は，著書《律原発揮》（1692・元禄5）において，1オクターブを12乗根に開いて12平均律を作る方法を発表した。これは，ヨーロッパの平均律とまったく同じものであった。

　しかし実際の音楽では，ヨーロッパの音律のような概念に基づく調律はほとんど問題とされず，いちおう標準と定められた律管によって調律を行い，その律管は1オクターブ内の12の音，すなわち十二律に応じて作られていたため，実際には，十二律の個々の名称が楽律の名称であると同時に音高の名称（音名）として用いられた。この十二律の楽律を定める方法は中国の三分損益によるが，実際には，順八逆六法と呼ばれる方法がとられたらしい。また十二律の名称も，中国の楽律名によらず，平安時代後期以来用いられた調名に基づく日本式の十二律名を用い，標準音としてはつねに壱越（いちこつ）を用いてきている。ただし，その壱越の音律は時代によって，その振動数に多少の異同があったものと考えられている。
→音名［日本］
執筆者：平野 健次

表1～表4

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

音律
おんりつ

音階中の各音の音程関係を規程する基準。音律に応じて実際に楽器の音高を決定することを調律という。

　中国、日本の音律は十二律である。音程は2音の振動数の比で決まるが、振動比3：2の完全5度を順に重ねると12番目の音がほぼ基準音と一致する。このことからオクターブ内に12の音を定めたのが十二律で、西洋のピタゴラス音律と同一である。方法は、管長の3分の1を交互に加減する三分(さんぶん)損益法であり、60律、360律まで求めた記録もある。十二平均律は西洋より早く明(みん)の朱載堉(しゅさいいく)が発見したが、すでに南朝宋(そう)（420～479）で試算されており、日本でも和算家中根元圭(げんけい)が1692年（元禄5）の『律原発揮』のなかで試みている。しかしこれらはすべて理論にとどまり、実際には12の律管で調律した。そのほかインドではシュルティと称し、弦の半分を9等分し、残りの半分を13等分して得られる22律が使われ、タイでは7律が、3/4音の使用を特徴とするアラビアでは、古くは9律や7律、現在ではメシャーカの考案した二十四平均律が使われる。インドネシアにはスレンドロ音階(ララス)、ペロ音階など5音、7音の調律体系があるが、統一的ではなく、逆に合奏楽器ごとの微妙な差異が尊ばれている。

　西洋音楽の音律理論は古代ギリシアのピタゴラス音律に始まる。求め方は十二律と同じだが、12番目の音は厳密には基準音より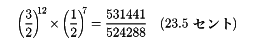

高く、その差を「ピタゴラスのコンマ」という。のちオルガヌムの発達とともに長3度、長6度の不協和が問題となり、一つの調体系のなかで主要三和音が協和する純正律が考案された。また中全音律では、大全音と小全音を平均した中全音（ミーン・トーン）により協和関係を近親調まで広げ、転調が容易にされた。しかしこれも、遠隔調への転調が進むにつれ、12の等しい半音からなる十二平均律に移行する。この平均律では転調が完全に自由となり、後期ロマン派から印象主義、十二音音楽に至る西洋音楽の隆盛がもたらされた。

［橋本曜子］

[参照項目] | 十二律 | 純正調

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

音律
おんりつ
temperament

音楽用語。音楽に使用される音高の相対的関係を，音響物理的に規定したもの。音の絶対的な高さは，発音体の振動数によって決定することができるが，音高の相対的な関係は，振動数の比率によって表わされる。振動比をどのような原理に基づいて規定するかによって，種々の音律が生じる。古代ギリシアでは，振動比2分の3の純正5度を重積することにより得られる音律 (ピタゴラス音律) が考えられた。しかしこれは長3度が 64分の 81という不協和な響きを生じるという難点から，3度が次第に重要視された中世にいたって，振動比2分の3の5度とともに，4分の5の協和的長3度を基礎とする純正律が用いられた。この純正律も転調に欠点があり，ルネサンス期には中全音律が考案され，さらに 18世紀には，オクターブを 12の半音に平均に等分する 12平均律が採用された (→平均律 ) 。東洋，日本では「十二律」といって「三分損益法」によって求められた音律が通用している。

出典　ブリタニカ国際大百科事典 小項目事典

普及版 字通

【音律】おんりつ

音の調子。

字通「音」の項目を見る。

出典　平凡社「普及版 字通」

世界大百科事典（旧版）内の音律の言及

【音階】より

…そのほかヨーロッパの諸民族にはなおいろいろの音階があるが，スコットランドなどにみられる5音音階(ペンタトニックpentatonic，図7)や増音程によって特性のあるジプシー音階(図8)は，芸術音楽にも取り入れられている。音律[西洋]【渡 鏡子】
【東洋】

［音階にあたる用語］
　諸民族それぞれの伝統にしたがって多種多様の音階が用いられており，東洋諸国の大部分ではそれを体系化しようとする理論を持っている。西洋の音楽理論でいう音階にぴったり当てはまる用語ではないが，音階に何かをつけ加えたような概念が用いられてきた。…

※「音律」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」