ホール効果（読み）ホールコウカ

デジタル大辞泉

ホール‐こうか〔‐カウクワ〕【ホール効果】

《Hall effect》電流の流れている細長い金属板に垂直に磁界をかけると、電流と磁界の両方に垂直な方向に電位差が現れる現象。1879年に米国の物理学者ホールが発見した。

出典　小学館

化学辞典 第2版

ホール効果
ホールコウカ
Hall effect

図のような形状の導体でx方向の電流密度を J_x とし，これと直角に B_z の磁場を加えると，ローレンツ力によって，J_x と B_z の両方に直角な電場 E_y が生じる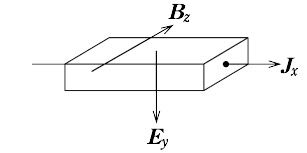．これは，アメリカの物理学者E.H. Hallによって発見されたため，ホール効果という．J_x，E_y，B_z の間には，

E_y ＝ RJ_x × B_z

の関係があり，Rをその物質のホール定数という．ホール定数と，単位体積中の伝導電子数n，電子の電荷eの間には，

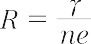
(γは散乱係数で，高純度のSiやGeでは3π/8をとり，金属や金属間化合物では1である)の関係がある．伝導にあずかる粒子が電子であるn型半導体などではR ＜ 0であるが，ほとんど満たされたエネルギー帯中で，正孔による伝導であるp型半導体などの場合はR ＞ 0となる．そのときはnを正孔の濃度Pで置き換え，eを－eとすれば，上式はそのまま成り立つ．以上は，伝導粒子が電子か正孔かの一方である場合を考えたが，両方によって伝導が起こっている場合は，より複雑となる．ホール効果は，とくに半導体において，伝導の性質を研究するうえで重要である．この効果の応用として，Ge，Siや，In-Sb，In-Asを用いた磁束計や，電力計，無接点ボリューム抵抗などがつくられている．

出典　森北出版「化学辞典（第2版）」

改訂新版　世界大百科事典

ホール効果 (ホールこうか)
Hall effect

導体に電流を流しながらこれと垂直に磁場をかけると，電流と磁場の両方に垂直な方向に電場が生ずる現象。1879年にアメリカのホールEdwin Herbert Hall（1855-1938）によって発見されたのでこの名がある。電流密度，生じた電場，磁場の方向をそれぞれx，y，z方向にとり（図），符号も含めたそれらの大きさをJ，E_H，Bとするとき，E_H/JBをホール係数という。ホール効果の原因は磁場の中を運動する荷電粒子に働くローレンツ力である。電荷qの粒子がx方向に速度vで動くとし，単位体積当りの粒子数をNとすれば，電流密度JはNqvである。z方向の磁場Bの中で粒子にはy方向にローレンツ力－qvBが働く。これにより粒子はy方向に動こうとするが，この方向は行止りであるため，この方向に垂直な両側表面に電荷がたまり，この電荷のためy方向の電場が生ずるのである。定常的には，ちょうどローレンツ力を打ち消すだけの電場E_Hが発生し，y方向への粒子の動きをおさえている。すなわち，

　－qvB＋qE_H＝0

であるから，E_H＝vBとなり，ホール係数R_Hは，

　R_H＝E_H/JB＝1/Nq

となる。ホール係数はとくに半導体での実験に際しての基礎データとして重要で，この符号から荷電粒子の符号，担体が電子か正孔かがわかる（図は担体が電子の場合）。さらにR_Hの大きさから担体の密度Nを求めることができる。ただし伝導電子と正孔の双方が同程度に電流に寄与しているときには，ホール係数の打消し合いが起こり，解析は複雑になる。
執筆者：黒沢 達美

図－ホール効果

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ホール効果
ほーるこうか
Hall effect

1879年にアメリカの物理学者E・H・ホールが発見した電流磁気効果の一種。電流の流れている半導体や金属の板に垂直に磁束密度Bの磁場をかけると、電流と磁場に垂直な方向に電場（ホール電場E_Hという）が生じ起電力が発生することをいう。

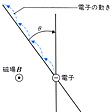
　n形半導体に電場Eと同時にそれと直角の方向に磁場を加えた場合、電子は電場と反対方向に平均速度v（＝μE）で移動する（μは電子の動きやすさの程度を示す移動度）。すると、電子は速度vと磁束密度との積に比例した力を、運動の方向と磁束の方向との両者に直角の方向に受けて、その運動方向がしだいに曲げられてくる。その結果、電子は弧を描きながら平均として電場と反対方向に対しある角度θをなす方向に進む。これは、半導体中では、電子はある程度加速されて移動すると、結晶格子あるいは不純物などに衝突して静止し、ふたたび振り出しに戻って同様の運動を繰り返しながら一定の平均速度で移動しているからである。このため、電子は図で左側に掃き寄せられるので左側が負に帯電し、電場に対して直角方向右向きの電場を生ずることになる。これをホール電場とよんでいる。また、半導体片の両側面に電荷が偏った結果として電圧が発生する。このとき発生する電圧をホール起電力とよぶ。

［右高正俊］

[参照項目] | 電流磁気効果 | ホール

ホール効果（n形半導体の例）〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ホール効果
ホールこうか
Hall effect

半導体や金属などの板に，ある方向 (たとえば直交座標系で x 方向) に電流を流し，それに垂直に静磁界をかけると，電流と磁界に垂直な方向に電場が生じ，この方向に電位差が生じる。これをホール効果という。電流磁気効果の1種。荷電粒子が磁界によるローレンツ力を受けて軌道が曲げられるため生じる。 1879年 E.ホールによって発見された。磁束密度を B ，電流密度を i ，ホール電場を E_H とすると，E_H＝R_HiB の関係が成り立つ。おのおのは直交座標において図のような方向をとる。 R_H は比例定数でホール係数と呼ばれ，物質の種類，温度などによって決る。 R_H の符号は，キャリアが電子なら負，正孔なら正であるため，キャリアの判別ができ，不純物半導体のn型，p型の区別をすることに利用される。さらにキャリアの密度を n ，電荷を e とすると R_H＝r/ne (金属の場合 r＝1 ，半導体の場合 r は1に近い値) となるため，ホール係数より密度も求められる。電流を一定に保てば，ホール電場 E_H は磁束密度 B に比例するため，磁束密度の測定に用いられ，これをホール素子磁力計という。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

ホール効果【ホールこうか】

細長い導体または半導体の板に電流Iを流し，電流に垂直な方向に磁場（磁束密度B）を加えると，電流・磁場の両方に垂直な方向に起電力Vを生じる現象。磁場方向の板の厚みをtとするとV＝RIB/tの関係があり，ここでRは材料の種類や不純物濃度によってきまる定数で，ホール係数と呼ばれる。電子の軌道が磁場の作用によって曲げられる（ローレンツの力）ため生じるもので，正孔による電気伝導の場合は起電力の方向が電子のときと逆になる。伝導の本性を調べる重要な手掛りとなり，またこの効果を利用した半導体素子（ホール素子）は磁場の検出・測定等に利用される。1879年米国の物理学者ホールE.H.Hall〔1855-1938〕が発見。
→関連項目クリッツィンク

出典　株式会社平凡社

法則の辞典

ホール効果【Hall effect】

金属試料片に電流 I を流し，これと直角方向に磁束密度 B の磁場をかけると，I と B のどちらにも直交する方向に電位差が生じる．これは1879年にホール（E. H. Hall）が発見した現象であるが，このときの電位差 V は，金属片の厚さ（磁場方向）を d とすると次のような式で表せる．

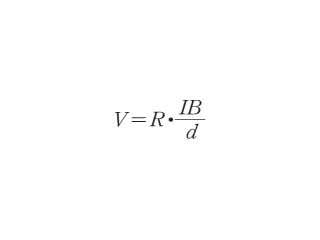
ここで R はホール係数＊と呼ばれるもので，金属の種類，温度によって異なる値をとる．ホール係数はキャリアの符号と密度によって決まるから，金属ならば電子，半導体ならば正孔の場合と電子の場合がともに存在する．

出典　朝倉書店

知恵蔵

ホール効果

半導体の単結晶に電界を加えて電流を流し、同時に電界に垂直な方向に磁界を加えると、それら電界と磁界の両方に垂直な方向に起電力が発生する現象。発生した電圧をホール電圧と呼ぶ。この起電力は、半導体中の電子及び正孔が、加えた電界と磁界の両方に垂直な方向にローレンツ力(運動する荷電粒子と電界及び磁界との相互作用によって生じる力)を受け、それぞれ、半導体結晶の片側に寄せられて、結晶面が負及び正に帯電するために発生する。

(荒川泰彦 東京大学教授 ／ 桜井貴康 東京大学教授 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」