精選版 日本国語大辞典 「沈降」の意味・読み・例文・類語
ちん‐こう‥カウ【沈降】
- 〘 名詞 〙
- ① 下方に沈んでいくこと。また特に、土地などが沈み下がること。沈下。
- [初出の実例]「日本海岸の土地は沈降若くは減少する所多し」(出典:日本風景論(1894)〈志賀重昂〉一)
- ② 沈みよどむこと。沈殿。
- [初出の実例]「他酸に溶解する銀液に塩酸を加ふれば、其塩酸銀に和して塩酸銀と為て沈降す」(出典:舎密開宗(1837‐47)内)
改訂新版 世界大百科事典 「沈降」の意味・わかりやすい解説
沈降 (ちんこう)
sedimentation
大量の液体中に微小粒子を混合してよくかきまぜ,粒子を液体中に均一に分散させたのち,混合液を容器中で静置すると,粒子の密度が液体の密度より大きければ粒子は重力により底に沈み,容器上方には粒子を含まない上澄み液ができてくる。この現象を沈降といい,気体中の粒子や液滴の場合でも同様である。沈降現象を起こす推進力は重力,粒子と液体との密度差,粒子の大きさなどであるが,このほかに遠心力,静電力を受けた粒子が流体中を移動するのも広い意味で沈降と呼ばれる。
密度が同一で大きさの異なる粒子群において,液体中に分散している粒子の濃度が希薄で粒子が互いの影響を受けず,かつ粒子径が容器の大きさに比べて小さく器壁の影響を受けないとみなせるならば,大きな粒子は小さな粒子より先に沈み,容器の深さ方向に濃度変化を生ずる。このような現象を自由沈降free settlingという。同じ密度の粒子間で,粒子径の大きいほうが小さい粒子より速く沈む現象は,沈降速度sedimentation velocityの差によるものである。いま粒子が流体中にあって,重力と浮力および粒子に働く抵抗力とがつり合った場合,粒子は流体中を一定速度で沈んでいくが,このときの速度vは次式で与えられる。
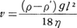
ここにρ,ρ′はそれぞれ粒子および流体の密度,ηは流体の粘性率,gは重力の加速度,lは粒子径を表す。
この現象を利用し容器内の一定深さの面における粒子濃度の時間的変化,もしくは一定時間経過後における容器の深さ方向の粒子濃度の変化を調べ,沈降速度と粒径との関係から,ふるい分級では測定できない100μm以下の粒子の粒径分布を求めることができる。これを沈降分析sedimetryという。
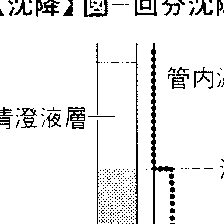
凝集性粒子あるいは粒子濃度がある程度以上大きな濃度で分散している混合液を容器中でよくかきまぜ均一にしたのち静置すると,時間経過とともに上方に清澄液層ができ,清澄液層と粒子混合層との間に形成された明りょうな境界面が下方に移動するのと同時に,濃い濃度層が底部から上昇する現象が観察される。この現象を干渉沈降hindered settlingといい,このときの清澄界面高さと時間との関係は回分沈降曲線で表される。その代表的な例を図に示す。沈降開始初期の清澄界面直下の濃度は懸濁液の初濃度に等しく,界面沈降速度は一定で,直線で表される。この区間を定速沈降区間と呼び,直線の傾きは初濃度における懸濁液中の粒子群の沈降速度を表し,初濃度が大きければ速度は減少する。図の圧縮点以降は減速沈降区間あるいは圧縮脱水区間と呼ばれ,清澄界面直下の濃度は深さ方向に連続的に時々刻々変化しており,これとともに界面沈降速度は減少して最終高さに漸近する曲線となる。さらに長時間放置すると界面高さは変化しなくなり,清澄液層と最終粒子沈積スラッジ層の二つに分かれて沈降を終了する。このときのスラッジ層の容積を沈降容積sedimentation volumeと呼び,粒子単位質量または容積当りのスラッジ容積で表した値は液体中の粒子充てん状態を示すもので,粒子の形,大きさとその分布,粒子間相互作用,粒子と液体の親和性,粒子表面の吸着物質の種類などに影響される。30分静置後の粒子1g当りのスラッジ容積をccで表したSVI(sludge volume index)もスラリーの沈降性を表す尺度として用いられる。沈降現象は鉱工業で沈降濃縮や清澄化などの固液分離に広く用いられており,回分沈降曲線はそれらの設計の基本となるものである。
執筆者:渡辺 治夫
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「沈降」の意味・わかりやすい解説
ブリタニカ国際大百科事典 小項目事典 「沈降」の意味・わかりやすい解説
沈降
ちんこう
sedimentation
沈降
ちんこう
subsidence
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
化学辞典 第2版 「沈降」の解説
沈降
チンコウ
sedimentation
分散系において,分散相の密度が分散媒の密度より大きいときに,重力のもとで沈下する現象.その密度の差が小さいときや分散粒子が小さいときには沈降速度が小さくなり,ブラウン運動による拡散速度に匹敵するようになると,事実上,沈降が認められない状態になる.これを沈降平衡という.分散相の密度のほうが分散媒の密度より小さい場合には,重力の方向とは反対に浮き上がるが,力学的には方向が反対になるだけで沈降と同様の法則に従う.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
最新 地学事典 「沈降」の解説
ちんこう
沈降
subsidence
地殻が広い範囲にわたって下がる運動。運動は鉛直方向に限られ,側方への変位を伴わない。隆起の対語。
執筆者:小島 丈児
出典 平凡社「最新 地学事典」最新 地学事典について 情報
栄養・生化学辞典 「沈降」の解説
沈降
世界大百科事典(旧版)内の沈降の言及
【地震災害】より
…日本の例では,濃尾地震(1891)における根尾谷断層が特に有名で,垂直方向のずれは6mにも達した。(2)隆起・沈降 上下方向に生じる地盤の変位である。(3)地すべり,山崩れ,崖崩れ,山津波 地盤が徐々に崩れる現象が地すべりである。…
※「沈降」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
1 花の咲くのを知らせる風。初春から初夏にかけて吹く風をいう。2 ⇒二十四番花信風...