ハミルトンの原理（読み）ハミルトンノゲンリ（英語表記）principle of Hamilton

デジタル大辞泉

ハミルトン‐の‐げんり【ハミルトンの原理】

ある系における物体の運動の経路は、経路全体で定義される作用量という積分量が極値をとるような経路に定まるという原理。ニュートンの運動方程式から導かれるものと同等になる。物体の運動を変分法の形式で表した物理学の基本原理の一つ。1834年にハミルトンが定式化した。

出典　小学館

改訂新版　世界大百科事典

ハミルトンの原理 (ハミルトンのげんり)
principle of Hamilton

古典力学において質点，または質点系の運動を定める法則，すなわち運動法則は質量×加速度＝力というニュートンの第2法則であり，これを質点の座標に関する2階微分方程式と考えて一定の初期条件のもとに解くならば質点の軌道が定められる。このように運動方程式そのものが運動法則をもっとも直接に表すのであるが，19世紀になって，これを別な形に述べることによってより統一的な原理にまとめる試みが次々と現れ，それを軸としてニュートン力学は解析力学にまとめられるようになった。そのような試みとしてダランベールの原理や最小作用の原理の例があげられるが，そのうちもっとも一般的で完全なものが1834年W.R.ハミルトンによって与えられたハミルトンの原理であり，解析力学の基本原理となっているものである。ハミルトンの原理は以下のように述べられる。

　質点系の座標x（1個の質点について三次元，n個の質点について3n次元のベクトル）が時刻t₁でx₁，t₂でx₂に固定されているとき，x₁とx₂を結ぶあらゆる可能な（滑らかな）軌道のうち，ニュートンの運動法則に従って実際に生起する質点系の運動の軌道は，系のもつラグランジュ関数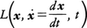のt₁，t₂を結ぶ積分が軌道の変分に対し停留値をとるという変分原理，すなわち，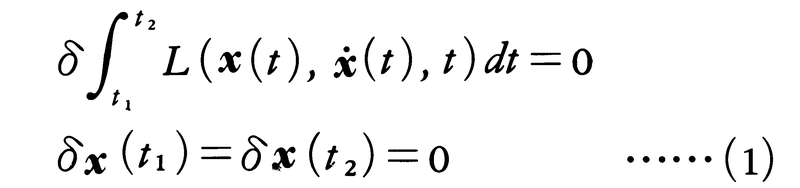

を満たすような軌道x（t）に限られる。系がポテンシャルの場で運動する場合，そのポテンシャル関数をU（x，t），また運動エネルギーをẋの二次関数T（ẋ）として，

　L（x，ẋ，t）＝T（ẋ）－U（x，t）

である。

　以下，この原理がニュートンの運動法則と等価であることを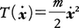の場合に示そう。軌道x（t）を各時刻において別の軌道x（t）にずらしたときの変分δx（t）＝x（t）－x（t）に対し，L（x，ẋ，t）の変化は，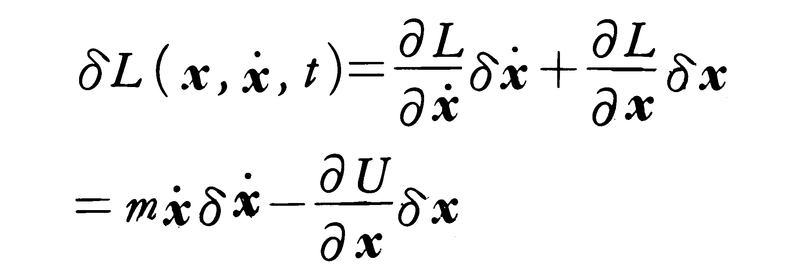

のように計算される。これを時間積分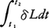に代入するとき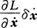，の積分は部分積分により，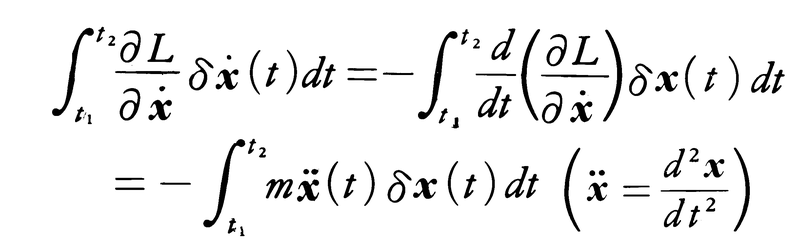

と書かれるので，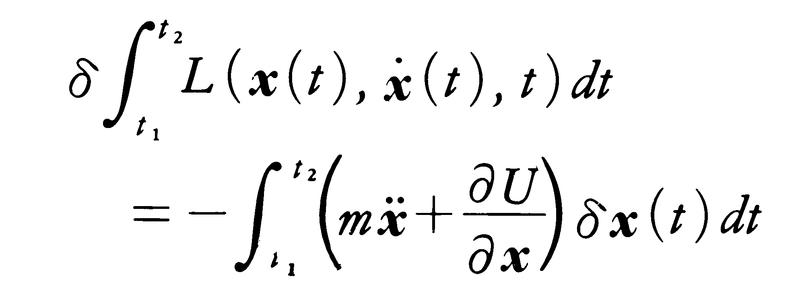

となり，これが任意の一次変分δx（t）に対し0となるというのが停留条件であるから，それを満足するx（t）は，上の積分のかっこの中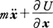が0となるもの，すなわちニュートンの運動方程式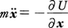を満たすものでなければならない。

　以上は，ラグランジュ関数とそれに対する変分原理から導かれるオイラーの方程式の形で述べられたハミルトンの原理であるが，解析力学ではいわゆる正準方程式を導く形がより重要な意味をもっている。それは次のような手続によりラグランジュ関数をハミルトン関数で置き換え，それに対する変分原理によって表現するものである。

　座標成分x_iに対する正準運動量成分p_iを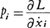で定義し，2f（f＝3n）個の変数x₁，……，x_f;ẋ₁，……，ẋ_fをx₁，……，x_f;p₁，……，p_fで置き換えれば，運動は2f次元の相空間で記述されることになるが，このときハミルトン関数H（p，x，t）を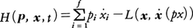，で定義する。このとき変分原理（1）に現れる積分は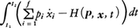，のようになり，変分問題は2f次元相空間における変分問題となる。この場合ハミルトンの原理は次のようになる（x_i＝q_iと書き，一般化座標の形式で述べる）。時刻t₁，t₂に対応する相空間上の2点（p，q）₁，（p，q）₂において座標成分q₁，q₂が固定されているものとする。これを結ぶあらゆる可能な（滑らかな）軌道のうち運動法則に従う軌道は変分原理，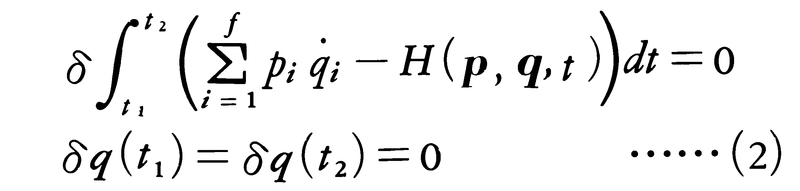

を満たすもの，すなわちハミルトンの運動方程式

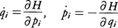に従うものに限られる。
執筆者：長谷川 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ハミルトンの原理
はみるとんのげんり
Hamilton's principle

イギリスの数学者・物理学者のW・R・ハミルトンが1834年に与えた力学の原理。力学系の実現される運動は、運動の経過全体に関するある量が極値になっているという条件によって特徴づけられていることを示した原理。この原理に基づいて運動を決定できるが、それはニュートンの運動方程式によるものと同等である。後者は微分形式で時々刻々の運動をその直前の状態から因果的に決定するのに対し、この原理は運動全体にわたる積分量に対して条件づけるので、あたかも運動が合目的的におこっているような表現になっているのが特徴である。

　力がポテンシャルから導かれる場合、運動の始まりと終わりの時刻の間の経路に沿ってラグランジュ関数の値が定まりその時間積分が得られる。経路を仮想的に微少変化させるとこの積分値も変わる。ハミルトンの原理は、これらの積分値が実現される運動に対して極値をとるということを述べた変分原理である。変分の際、独立な変分量のとり方によってラグランジュやハミルトンの方程式を導くことができ、また力学以外の物理法則もこの形に書かれるものがあり、包括的な定式化と考えられる。

［永田　忍］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ハミルトンの原理
ハミルトンのげんり
Hamilton's principle

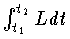力学における変分原理の1種。時刻 t₁ と t₂ の間の実際の運動経路は同じ両端点を通る経路のなかでラグランジュ関数 L の時間積分 が最小になるという原理。これからラグランジュの運動方程式が導かれる。全エネルギーが一定な経路だけに限って変分をとれば最小作用の原理に一致する。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

ハミルトンの原理【Hamilton's principle】

ハミルトンはそれ以前のモーペルチュイやオイラー，ラグランジュなどの導いた結果を整理して，質点系に対して V をポテンシャルエネルギー，T を運動エネルギーとしたとき

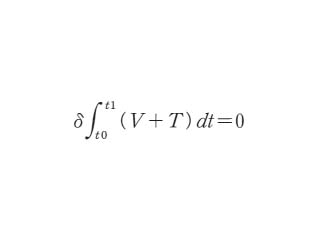
となるが，現実の運動の系に対しては，これが成立しなければならないとした．

ハミルトンの原理【Hamilton's principle】

始点と終点の二つの配置の間の配置空間中を運動する保存系の運動の経路は，ラグランジュアン（T-V）の時間積分が始点と終点との間を運動する時間が，他の経路に比較して最小となるものとなる．

出典　朝倉書店

世界大百科事典（旧版）内のハミルトンの原理の言及

【最小作用の原理】より

…ここで作用積分とは，質点の運動量p(t)をその描く軌道q(t)に沿って積分する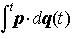，のことを意味していた(tは時間)。のちのハミルトンの原理からみてモーペルテュイの主張が正しいのは，質点のもつハミルトン関数Hがp(t)，q(t)以外に直接tに依存しない形式の場合，すなわちHが一定値E(運動エネルギーTと位置エネルギーUの和)，言い換えれば軌道がすべてこのような等エネルギー面上にある場合である。実際，このとき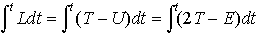となり(L＝T－U,H＝T＋Uはそれぞれラグランジュ関数とハミルトン関数)，したがって運動を決める変分原理は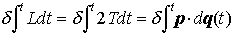，のように，モーペルテュイの形式とハミルトンの形式とが一致する。…

【ハミルトニアン】より

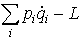…L(q_i，_i)＝K－Vからp_i＝∂L/∂q_iを定義し，p_iをq_iに共役な運動量という(_iの･は，q_iの1階の時間微分の意味)。_iをq_iとp_iで書き表し，をq_iとp_iの関数として表したH(q_i,p_i)をこの力学系のハミルトン関数，あるいはハミルトニアンと呼ぶ。Kが_iの二次斉次式のときはHは系の全エネルギーに等しく，ハミルトニアンは系の全エネルギーを座標と運動量で書き表したものである。…

※「ハミルトンの原理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」