暗号（読み）あんごう（英語表記）cryptography

精選版 日本国語大辞典

あん‐ごう ‥ガウ【暗号】

〘名〙

① あらかじめ打ち合わせておく、合図のためのことば。あいことば。

※寛永刊本江湖集鈔（1633）一「暗号とはあい言ば也」 〔堯山堂外記〕

② (━する) 符号で定めた合図。また、ある取り決められた方法で合図すること。

※航米日録（1860）二「ホーハタン船上にて暗号す、砲を発し且流星火を放つ」

③ 特に、第三者に内容がわからないように意志をこっそり伝えるため、当事者間で取り決めた符号、または、方法。

※葬列（1906）〈石川啄木〉「今度はホーホケキョとやる。（これは自分の名の暗号であった）」

出典　精選版 日本国語大辞典

デジタル大辞泉

あん‐ごう〔‐ガウ〕【暗号】

通信の内容が相手以外にわからないように、当事者の間だけで決めた記号。軍事・外交・警察・商業などで使われる。
[類語]符丁・合い言葉・コード・パスワード・合図・信号・シグナル・サイン・手招き・目配せ・ウインク・片目をつぶる・目交ぜ・目印・合い印・標識・狼煙のろし・烽火・号砲・警鐘・半鐘・振鈴

出典　小学館

日本大百科全書(ニッポニカ)

暗号
あんごう
cryptography

広い意味では、通信の内容を秘匿(ひとく)したり認証するために使うことば、ならびにその技術。暗号という用語は中国から入ったもので、西南戦争（1877）ごろまでは、合いことばもしくは合図といった意味に使われた。一般的には、文字で書かれたものを対象にしている。日本の兵法書には、暗号に相当することばとして「計策文認(したた)め様の事」とある。

［長田順行］

原理と形式

暗号の原理は、ことばの仕組みを考えてみるとよくわかる。ことばは、決まった音（文字）が決まった順序に並び、それが決まった意味をもつわけであるから、これを第三者に秘匿する方法は、このようなことばの仕組みの一つ一つに、ある操作を人為的に加えること以外にはない。これをまとめると、(1)換字(かえじ)式、(2)転置式、(3)分置式、(4)約束語、(5)隠文式、(6)混合式の六つの形式となる。

(1)換字式substitution　もっともよく使われる暗号の形式である。その方法を、欧米ではサイファーcipherとコードcodeに分ける。サイファーとは、原文を文字単位に別の文字や符号で置き換えるものをいう。ポーの小説『黄金虫(こがねむし)』の暗号文はその一例である。コード（略号）とは、単一の文字、音節、単語、句あるいは文のように各種各様の長さのものを、一定の長さの無意味な文字群または数字群で置き換えたものをいう。身近なものには郵便番号がある。語句とそれを表す記号の対応を辞書のように一冊にまとめたものをコード・ブック（暗号書）という。

(2)転置式transposition　逆順に書く方法、図形を利用して原文を書き込み、別の方向に鍵(かぎ)の指示によって順次に書き出して暗号文とするといった方法などがある。なお、OLD ENGLAND（老いたるイギリス）を並べ替えて、GOLDEN LAND（黄金の国土）にするといったアナグラムも技法的には転置式とよべなくもない。

(3)分置式　身近な例には、単語の第1音節と第2音節の間に「ノサ」の2音を挟む「ノサことば」がある。また、折句(おりく)（アクロスティック）などもそうである。たとえば、紀貫之(きのつらゆき)の「小倉山　峯(みね)立ち鳴らし　なく鹿(しか)の　へにけむ秋を　しる人ぞなき」という和歌には、各句の初めに「おみなへし」が隠されている。実際には、新聞の文字に秘密インキで印をつけるとか、一定の窓を切り抜いた型紙を使うなどの方法が用いられる。

(4)約束語　隠語ともよばれる。ロッキード事件に関連して明らかにされた、以下のような隠語の数々はそのよい例である。

〔ロッキード社の隠語表（部分）〕
●日本関係
GOPHER（ジネズミ）＝川崎重工
IVY（ツタ）＝全日空
SCALPEL（解剖用メス）＝航空貨物会社
TAT（インド産小馬）＝日本
TAW（おはじきの石）＝東京
ROW（列）＝丸紅
HYENA（ハイエナ）＝明電舎
PELICAN（ペリカン）＝日本人およびドイツ人
MOW（干し草置き場）＝自由円
MUD（泥）＝日本側持ち分
APPETIZER（前菜）＝普通円
CAVERN（洞窟）＝日本円
●外国関係
COSMOS（宇宙）＝ポンピドー前仏大統領
POINTER（猟犬）＝ウィルソン前英首相
HALIBUT（大ヒラメ）＝エアハルト元西ドイツ外相
POWDER（火薬）＝ブラウン元英外相
LITTLE BEAST（小さな獣）＝パン・アメリカン航空
HURRICANE（熱帯性暴風）＝金銭の授受

　合いことばや符丁(ふちょう)なども約束語の一種といってよいだろう。約束語が一つの文章になっているようなものは隠語文とよばれる。太平洋戦争で「作戦開始日は8日とする」という意味に使われた「ヒノデハ　ヤマガタトス」という日本陸軍の例は、海軍の使った「新高山(にいたかやま)登れ」とともに有名である。

(5)隠文式　比喩(ひゆ)を使ったもっとも巧緻(こうち)性に富む暗号。『日本書紀』の諷歌(そえうた)や童謡(わざうた)の例もそうであるし、ギリシア神話のスフィンクスの謎(なぞ)かけなど、なぞなぞには隠文式のものが多い。

(6)混合式　代表的なものは、換字式と転置式の組合せである。一般的に強度は増すが、暗号作業は複雑となる。推理小説では、解決の意外性をねらう目的から、分置式や隠文式などのような暗号らしくない暗号を、組合せの最後に使うことがある。

［長田順行］

暗号解読の基礎資料

暗号の解読には、原文に使われた国語の一般的な知識のみならず、計量的な基礎資料が必要である。

　文字の使われる割合を百分率で示したものを頻度という。仮名で書いた日本語では、いうんしのよかとくつ……といった順に頻度が高い。これらはあくまでも一つの統計結果であって、実際の暗号文では、その順位はある程度変わる。文字の頻度の特徴は、換字式と転置式の形式判定のみならず、サイファーの各種の方式を判定し、最終的な解読に至るもっとも有力な武器となる。また、文字の続きぐあい（連接特徴）では、英語の場合は、th, he, in, er, re,……の順に、日本語では、よう、ゆう、せい、とう、てい、……の順によく使われる。これらの特徴は、転置式のみならずサイファーの解読にもきわめて有効である。単語についても、その頻度や連接には特徴がある。もちろん、この統計調査はたいへんな作業であるが、コード・ブックの作成、あるいは解読には欠かすことができない。

［長田順行］

暗号の歴史

暗号の起源は、人類がことばをもったときから始まるといってよい。初めはことばそのものが、それを知らない人にとっては暗号であったであろうし、言い換えそのものが、隠文式や約束語としての役割を果たしたであろう。一般的な暗号を使った例や暗号記法について述べた記録は、古代エジプトやギリシアの時代まで下らなければならない。ギリシアでは、スキュタレーとよぶ棒を使った転置式の暗号の例があるし、戦国時代の「字変四十八の法」と同じ構成の表が、のろしによる文字の伝送に使われている。ローマでは、カエサルの換字式の暗号が有名である。しかし、暗号の急激な進歩は、近代外交の発祥地である14～15世紀のイタリアを中心に始まる。

　当初は、約束語を表にしたもの（隠語表）が外交用に使われたが、しだいにコードがその主流となり、フランスのルイ13世、14世の治下では現在のコード・ブックの形態まで進歩した。それから何世紀もの間、コード・ブックは外交用暗号はもちろん、商業用暗号や軍事用暗号の主要な方式となった。

　サイファーは、一つの換字表を使っただけでは簡単に解読されることが知られるにつれて次々にくふうされ、最終的には、原文の一つ一つの文字を換字表を変えながら別の符号や文字に置き換えるところまで進歩した。通常、換字表の数は文字や符号の数と同じ（英語ではアルファベット26、数字ならば10）で、それぞれの換字表は一定の規則的な文字配列のものが使用される。なかでも「ビジュネルの正方形の表」は有名である。この方式は、欧米では換字表の数に着目して多表式とよばれるが、日本では換字表の選択に鍵(かぎ)を使うところから乱数式（乱字式）とよぶ。この乱数を一冊にまとめたものが乱数表（乱数帳）である。第二次世界大戦のころから、コード・ブックと乱数式の二つの方式はあわせて一つの暗号方式として使われるようになる。ミッドウェー海戦当時の日本海軍の「D暗号」もその一例である。

　暗号機というのは、換字式や転置式のある方式を機械化したものである。第二次世界大戦中に使用されたドイツのエニグマやアメリカのM209は、原理的には多表式であるし、1977年にアメリカ政府の暗号規格として採用されたDES(デズ)暗号Data Encryption Standardは、混合式を、進歩した計算技術と半導体技術によって具体化したものである。

　なお、現在では、ほとんどの国が通信攻撃（暗号解読もその一つ）と通信防衛を任務とする組織をもっている。このことは、戦時、平時を問わず、暗号戦争がいまもなお続いているということを物語っている。

［長田順行］

暗号とコンピュータ

暗号とコンピュータは深く関与している。コンピュータの揺籃(ようらん)時代にも、イギリスの数学者チューリングらが1943年に完成させた暗号解読用の真空管計算機（コロッサスColossus）があった。コンピュータの進歩とその利用形態の発達により暗号の様相も変化してきている。

［西村和夫］

近代的な暗号技術

情報理論の進歩は暗号の理論を飛躍的に進歩させた。とくにアメリカのシャノンが1949年に発表した理論は、現在でも役にたっている。その理論によれば、ある文字数以上の暗号文は、なんらかの方法によって解読されてしまう。ただしこの文字数は、暗号の方式と言語の特性によって異なり、使い捨ての乱数表を用いた方式では無限大になる（つまり解読できない）。また、暗号の安全性の尺度として、解読に要する作業量（四則演算の回数など）が重要であることも指摘している。

　現代的な暗号が古典的な暗号と技術的に異なるおもな点は次の三つである。

(1)処理単位が文字からビットになった――暗号化（組立て）と復号（翻訳）の処理において、古くは文字を操作の対象にしていたが、文字を二進符号で表したときの各桁(けた)（ビットという）を対象とするようになった。この傾向は暗号機の登場によって始まり、コンピュータでの処理が盛んになるとともに顕著になった。ビットのように細分化した要素についての暗号文の解読は、たとえばジグソー・パズル（文章）の一片（文字）をさらに細かく刻んだもの（ビット）を復原しようとするのと同じように、困難な作業となる。

(2)処理の能率が大幅にあがった――暗号解読にもコンピュータを利用することで、試行錯誤が手軽にかつ高速に行えるようになった。そのため、暗号化や復号の処理もコンピュータを使ってより複雑なものにしなければならない。

(3)安全性を計算量に拠(よ)るようになった――従来の複雑な暗号でも、その方式を推定されると、解読の鍵(かぎ)を見破られる可能性が大きくなり、安全とはいえなくなった。したがって、解読が原理的には可能でも、実際に解読しようとすると、最高速のコンピュータを使っても何万年もかかるような、計算量を重視した暗号が考案されている。

［西村和夫］

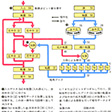
DES

アメリカの暗号規格であるDES方式は古典的な手法を現代的な思想で集成したもので、56ビットの鍵を用い、64ビットのデータを処理（暗号化と復号）する。処理は16回の単一操作の繰返しからなり、各操作での手法として、ビット単位の転置と加算および換字を行う。転置には、ビットを重複させて数を増やすもの（拡大転置）と、数ビットを削減するもの（縮小転置）とがある。換字は6ビットごとに行い、4ビットに縮小する。これは表を引くことで実現され、この部分（S箱という）がとくに解読を困難にしている。暗号化と復号には同一の鍵を用い、処理もほぼ同じである（違うのは、鍵の回転を右回りにするか左回りにするかだけである）。

［西村和夫］

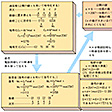
公開鍵暗号

ディフィーW. DiffieとヘルマンM. E. Hellmanは1976年に画期的な暗号の構想を発表した。その斬新(ざんしん)な点は、暗号化と復号の鍵を異なったものにすることで、これだけのことで、さまざまな長所が生じる。復号の鍵は秘密にしなければならないが、暗号化の鍵は公開して電話帳のようなものに載せることさえできる。したがって、多数の送信者が、ある受信者に同一の鍵で暗号化した通信文を送ることができる。しかもそれを復号できるのは、秘密の鍵を隠しもっている受信者だけである。これによって、特定の鍵を送受信者の間でひそかにやりとりする必要がなくなる。また、集団のなかで交信するときに各個人が秘密に保管しなければならない鍵の数も、いままでは交信する人の数だけ必要であったのが、各自の復号用の鍵だけですむ。

　もし暗号化と復号の処理が、逆に組み合わせてもうまく働くならば、署名をすることもできる。つまり、原文を（秘密の）復号用の鍵を使って暗号化した通信文にして送り、受け取ったほうは公開されている暗号化用の鍵を使って復号することによって原文に戻すのである。この通信文をつくれるのは秘密の復号の鍵をもっている人だけなので、署名（つまり捺印(なついん)）したのと同じ効果がある。したがって、二者が互いに相手の暗号化の鍵を知っていれば、署名付きの秘密通信を交わすこともできる。署名は、敵による攪乱(かくらん)を防いだり、商取引上の証拠とするために重要である。

　ディフィーとヘルマンが公開鍵暗号の構想を発表したときには、まだ具体的な方式が考案されず、いわば絵にかいた餅(もち)だったが、その後いろいろな具体的方式が提案されている。いくつかの方式は整数論を応用したもので、大きな整数による割り算の余りに関する演算を行う。これを法modulusのもとでの演算といい、たとえば60を法とすれば127mod60＝7となる。この代表的な方式としてRSA法があり、これを解読するには大きな整数（200桁）を素因数分解しなければならないが、それはほぼ不可能である（毎秒1億回の演算をしても100万年かかる）。RSA法のほかにも、秘密の通信だけができる方式、署名だけができる方式、さらにDESなどで用いる鍵の決定だけができる方式などもある。公開鍵暗号は電子メールや電子マネーなどに使われるようになってきた。

［西村和夫］

　1999年に複数台のコンピュータを使ってDESが解読された。そこでより安全性を高めるため、DESを3回繰り返すトリプルDESが考案された。

　その後、DESの後継としてAES（Advanced Encryption Standard）という暗号化技術が登場した。これは、最大256ビットのデータ長を使うためDESよりも安全性が高く、2001年にはアメリカの標準暗号方式として採用された。そのほかに、インターネットで広く使われるRSAやNTTが開発したFEAL（Fast Data Encipherment Algorithm）などもある。

［編集部］

『長田順行著『暗号』（1979・ダイヤモンド社）』▽『『コンピュータ・サイエンス』（『bit』別冊・1980・共立出版）』▽『デイヴィッド・カーン著、秦郁彦・関野英夫訳『暗号戦争』（ハヤカワ文庫）』▽『一松信著『暗号の数理』（講談社・ブルーバックス）』

[参照項目] | シャノン | チューリング | 乱数表 | ロッキード事件

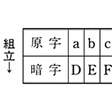
カエサル（シーザー）の換字表

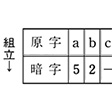
ポー『黄金虫』の換字表

字変四十八の法（戦国時代）

コード・ブック（暗号書）の例

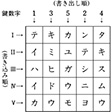
鍵式図形転置の例

ビジュネルの正方形の表（多表）

DES暗号の概要

公開鍵暗号（RSA法の概要）

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

暗号【あんごう】

秘密通信のため当事者間のみの約束に従って原通信文（平文(ひらぶん)という）に特定の変形を加えること。ときに暗号によって作られた暗号文を暗号ということもある。変形の手法は原理的に２種類に分かれる。（１）換字式では，平文の文字，文字群，音節，語句などを他の記号，文字などに置き換える。（２）転置式では，平文の文字の位置を一定の規約（キー）に従って変えていく。それぞれ多くの方法があり，両者の組合せ方式もある。軍事・外交・商業上によく用いられる暗号書（コードブック）とは，何万という文字や記号の置換えリストを辞書形式に作ったもので，通信者相互が使用法を約束して暗号文の作成，翻訳に利用する。
→関連項目共通鍵暗号方式｜公開鍵暗号方式｜コード（情報）｜ブラック・チェンバー

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

暗号
あんごう
cryptology

秘密通信を行うための方法や装置に関する科学。主として戦略に，ときには産業界でも，使用される。サイファー暗号とコード暗号に大別され，前者はさらに転字式と換字式に分けられる。コード暗号は換字式の一部と考えてもよい。暗号装置には，手動式から電動式にいたるまで種々のものがある。歴史的にみれば，古くはギリシアのスキュタレー方式，ローマのカエサル方式があり，近代暗号発祥の地イタリアでは，15世紀の前半に最初のコード集である「ベネチアのコード集」が使用された。次いで 16世紀の「ビジュネル暗号」，フランスの「2冊制コード集」が現れ，17世紀に入ってイギリスの F.ベーコンが2文字符号による通信法を導入，今日の二進符号化にまで発展した。近年では電子回路による自動化が標準となった。 1976年に，暗号化の鍵と復号の鍵とを別にする公開鍵暗号系が発表され，電子通信の秘密保持，プライバシー保護，文書の正当性認証などに大きな影響を与えつつある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典 第２版

あんごう【暗号】

甲乙両者が連絡通信を行う場合，その内容を第三者に秘匿する手段を暗号という。ときとして暗号によって作られた暗号文を暗号ということがある。また連絡通信そのものを秘匿する手段も考えられ，この手段をも含めて広義の暗号という。
［暗号の歴史］
　暗号は古くから使用されたもので，プルタルコスの《英雄伝》にはペロポネソス戦争(前431‐前404)で活躍したスパルタの将軍リュサンドロスが出先の司令官との連絡にスキュターレscytaleという1本の棒を使用する暗号を用いたと記されている。

出典　株式会社平凡社