単位(読み)タンイ(その他表記)unit
精選版 日本国語大辞典 「単位」の意味・読み・例文・類語
たん‐い‥ヰ【単位】
- 〘 名詞 〙
- ① 長さ、重さ、量などの数量を計算するときの基準となるもの。また、その数値。長さのメートル、重さのグラムなどの類。
- [初出の実例]「理家。凝流体の異重を比例するに餾水を単位とし之を比較の原に資り物体受熱の度も亦餾水受熱の度に比較す」(出典:舎密開宗(1837‐47)外)
- ② ( 一般的に ) 物事の比較計算の基となるもの。
- [初出の実例]「社会は一個人を単位(タンヰ)として、独立独行を主とすなるに」(出典:内地雑居未来之夢(1886)〈坪内逍遙〉三)
- ③ 仏語。禅宗の僧堂の座位。すなわち座席のこと。その座席の上に名札がはってある。
- [初出の実例]「蒲団常畱二単位一」(出典:永平道元禅師清規(13C中)弁道法)
- [その他の文献]〔勅修百丈清規‐六〕
- ④ ひとつの位。ひとけた。
- ⑤ 卒業などの資格を算定するために用いられる学課履修計算の基準。昭和二二年(一九四七)以降の学制下で、高等学校では一学年に三五単位時間の授業を一単位とし、大学では一五時間から三〇時間までの範囲で大学が定める時間の授業を一単位とする。
- [初出の実例]「耕二は大学で〈略〉支那語は格別理由もなく、思いつきで単位を取ってみる事にしたものであったが」(出典:春の城(1952)〈阿川弘之〉一)
改訂新版 世界大百科事典 「単位」の意味・わかりやすい解説
単位 (たんい)
unit
unit of measurement
マルクスの大著《資本論》の初めのところに〈1エレの麻布〉という表現がある。そこにどんな経済学的意味があるのか,また,なぜ麻布が例にあげられるのかは今は問わないが,もう一つの疑問〈エレとは何か〉は,ここでの検討の対象になりうる。エレは,布地などの寸法を測るための〈単位〉の一種だからである。
さて,エレに限らず,メートル,秒,アンペアなどの多種類の単位があるが,それらの意味や機能を考える前に,〈物事を数量的に表現するためのさまざまなことば〉をひとまとめに吟味しておくことにしよう。例えば,うそ八百,万巻の書,1杯のコーヒーといったいいならわしには,それぞれ独特な味わいが感じられるが,まず,うそ八百を検討してみる。この八百は,数の800のみでなく〈多数〉をも意味するので,うそ八百は〈うその多いこと,うそばかり〉を意味する。これを〈比率〉とみなして〈1000件の発言のうち800件,すなわち8割はうそ〉と解する人もあろうが,その種の比率を使うのなら〈千三(せんみつ)(1000のうち3だけはうそでない)〉や〈万八(まんぱち)(1万のうち8だけはうそでない)〉のほうが現実感に富んでいるのではなかろうか。万巻の書の万も,1万と多数の両方を意味するが,1万冊の本というと,個人でも意欲と投資しだいで所有できそうな蔵書規模であるから,この万という数は,手ごろというか小憎らしいというか,巧みに選ばれているといえそうである。
ところで,1万巻,1万冊の本というときの〈巻〉や〈冊〉は,比率を表すものではなく,現実の事物の件数,個数を表している。1杯のコーヒーの〈杯〉,12人の弟子の〈人〉も同類である。では,長さ3mの鉄棒の〈メートル〉,質量2kgの金塊の〈キログラム〉も同類であろうか。
これまでにあげた表現用語のうち,メートルとキログラムは,比率や件数,個数を表すことばとはやや違った機能をもっており,他の多数の類語(平方メートル,アンペア,パスカル,アンペア毎平方メートル,キロメートル,エレなど)とともに単位と呼ばれる。要約していえば,単位とは,〈量を測定するために基準として用いる一定の大きさの量〉である。うそ八百,万巻の書,1杯のコーヒーといった表現には,厳密な意味での〈単位〉の考え方は含まれていない。
単位の機能
メートル,キログラム,アンペアのような〈単位〉と,冊,巻,杯,人のような〈単位でないもの〉との違いは,どこにあるのだろうか。その核心は,前述の基準として用いる一定の大きさの量であるかどうかにかかっている。メートルは,長さを測定するために基準として用いることのできる,十分に一定な(時,所,場合によらず一定な)長さだが,〈冊〉は,一定の内容,もしくは価値をもっていない。そして,そもそも〈冊〉は,何かを測定するための基準として用いることのできる量ではない。〈冊〉は,測定やそのための単位とは別系統のことばなのである。それに比べると〈杯〉は,コーヒーその他の液体や粒体の分量を表現するときに使えることばではある。しかし,基準として用いることのできる一定性を備えてはいない。アメリカンコーヒーのカップ1杯とエスプレッソのデミタス1杯とは,まるで違っている。
話をメートルに戻すが,今,ある鉄棒の長さが3mだという記述がなされたとすると,この記述には次のような事柄がたたみこまれていると考えてよいのである。まず,ここでは〈長さ〉という〈量〉が問われていること,次に,この量の測定がすでになされていること,この量については単位,すなわち基準として用いる一定の長さがすでに定められていること,その単位の名称は〈メートル〉であること,そして,当の鉄棒の長さは1mという長さの3倍に相当すること。以上をまとめて〈鉄棒の長さL=3m〉と,(量)=(数値)×(単位)の形に記述するわけで,単位というものの機能は,この記述に全部ぬりこめられているといえる。1冊の本,1杯のコーヒーといった表現と長さ3mの鉄棒といった表現との違いも,ここで明りょうに理解されるであろう。
単位の歴史
酒などの分量を杯何杯とか樽何杯とかのことばで表現することは,人間が家族や部落を構成して社会的な営みを始めたのとほとんど同じ時期に開始されたに違いない。そこには単位の考えの芽生えが認められるし,現に,近代社会においても,杯,ジョッキ,樽などの〈器〉を表す単語が,そのまま体積の単位の呼名に採用されている例は数多く認められた。それらは,量を測定するために基準として用いることのできる量を代表していたかもしれないが,一定の量を代表するものではなかった。なぜなら,わが家の杯と隣家のそれ,また,わが部落の樽と他の部落のそれが,同じ分量の酒を盛るようにつくられているとは考えられない,つまり,器に入る液体の体積が一定であるとは考えられないからである。
時代が進み,社会的な営みが大規模かつ複雑なものに移り変わるにつれて,単位はしだいに緻密(ちみつ)な内容をもつようになった。器で体積の単位を決めるという発想は昔のままであるにしても,当の器を1種類に指定するとか,器の形や寸法を指定するとか,いろいろなくふうや申合せによって一定の体積を実現しようとする傾向が生じた。中国の各時代の嘉量,17世紀のドイツの数学・天文学者J.ケプラーがつくった枡(ます),日本で豊臣秀吉の時代に制定されたと解されている京枡は,形と寸法の指定された体積標準器の例であって,体積の単位の歴史のうえで,技術,行政のどちらの面からみても意義深いものとされている。これらの標準器では,形が円筒,または直方体と指定され,寸法(直径と深さ,あるいは3辺の長さ)も細かく指定されていて,標準器が具現する体積は,当時の社会の要求に十分こたえる程度に一定であると判断されていた。
ところで,ここに例示したような史上の標準器や,それによって具現される単位については,遺物や古記録による研究がなされており,例えば,ある単位と,それ以前または以後の単位との相互関係などが,綿密に調べられていることもある。また,体積の標準器の場合には,その寸法がどのような〈長さの単位〉に基づいて定められているか,つまり,体積の単位と長さの単位とがどういう相互関係にあったかが論証されている場合もある。
こうした歴史的研究は,いくつかの単位の相互関係を明らかにした反面,諸単位のとめどもない多様性をあばき出すことにもなった。人の足の寸法に由来するといわれた長さの単位(イギリス,アメリカのフートfoot。ドイツのフースFussその他),人が両手を広げたときの左右の指先の間の寸法に由来するといわれた長さの単位(日本,中国のひろ(尋)。イギリス,アメリカのファゾムfathomその他)のたぐいは,それぞれの由来のあいまいさに加えて,各国,各地方で,各時代に,また職業分野ごとに無秩序に標準の尺度がつくられたため,はなはだしく多様なものになってしまった。《資本論》のエレも,元来は人のひじから指先までの長さに基づくドイツ系の単位なのだが,実態は複雑だったから,マルクスは同書の巻末に諸単位の一覧表を掲げて比較の便に供しなければならなかった。日本の旧単位〈尺〉にしても,建築などに用いる曲尺(かねじやく)のほかに和裁用の鯨尺があって,二本立ての形になっていた。
どの国,どの地方,どの職業分野に属するかにかかわりなく,だれもがいつなりと使うことのできる単位を制定しようという考えは,もちろん古くからあったが,それが全世界的な規模で具体化され始めたのは,フランス革命の直前のころであった。フランスは,学識者を集めて対策を検討した結果,人類共有の物体である地球の寸法に基づいて長さの単位メートルを定めるという卓抜な方針をたて,その実現に必要な測量や他の従属的な単位を決めるのに必要な実験を精力的に開始した。時代は18世紀の末に近づいていた。
メートル法の成立と普及
18世紀末の時代の特徴は,自由,平等,博愛の理念やフランス革命の動向の中にのみみられるものではなく,イギリスからヨーロッパ大陸へ波及した産業革命の推移,それと並行する資本主義経済の成熟と広域化などとの関連においてもとらえられなければならないが,より具体的にみれば,交通(とくに航海)や通信の技術と運用制度の高度化が開始されて,多数の人の移動,大量の物資の輸送と交易,そして多彩な情報の交流が可能になった点などにも,この時代の特色を認めることができるであろう。地域,職域を超えた単位の統一という発想は,まさしくこれらの特色に呼応して顕現してきたのであるが,その実行にあたって,特定の先進国の利益に通ずる要素がきびしく排除され一挙に全地球的な構想がたてられたのは,史上まれな快挙であったと評してよい。この卓抜な構想の成立にもっとも力強く寄与したのは,I.ニュートンの力学やA.C.クレーローの地球形状論をはじめとする高度な科学的知見の集積であった。
構想の要点は,(1)地球子午線の全長を新たな測量によって確定し,その長さの1/40000000を長さの単位に選び,それをメートルと呼ぶこと,(2)メートルの1/10に相当する長さを1辺とする立方体の体積を考え,氷が融解する温度においてこの体積を占める蒸留水の質量を確定し,それを質量の単位に選び,グラーブ(のちにキログラム)と呼ぶことの二つであった。(1)のための測量は,スペインのバルセロナからパリの東をかすめてドーバー岸のダンケルクまでについて実行され,担当者ドランブルJ.B.J.DelambreとメシャンP.F.A.Méchainは,革命期の騒乱に悩まされながら1792年から6年余を費やしてこれを完遂した。一方,(2)のための実験は化学者A.L.ラボアジエを中心として92年に開始され,結晶学者アユイR.J.Haüyの協力下で着々と進められたが,ラボアジエが処刑された94年に中断され,2年後ルフェーブル・ジノーL.Lefèvre-GineauとファブローニJ.V.Fabbroniの手で再開されて,〈氷が融解する温度において〉ではなく〈水の密度が極大となる温度において〉の質量を単位に選ぶことや,名称をグラーブからキログラムに改めることを承認して99年終結した。これらの成果に基づいて作製されフランス文書館(アルシーブ)に納められた標準器は,〈アルシーブのメートル〉〈アルシーブのキログラム〉と呼ばれた。
これらの新単位は,万国博覧会などを通じて,また測地学や地磁気学の研究の広域化につれて,徐々に,しかし確実に各国で受容されることとなり,1875年にメートル条約が成立し,新単位のいっそうの普及と拡充をはかるための国際的な合議体(国際度量衡総会など)や中央機関(国際度量衡局)が編成された。日本は85年にこの条約に加入した。条約成立後の重要課題は,新単位を具現する標準器を製作して加入各国に配布することであった。白金90とイリジウム10の合金を材料とするメートル原器およびキログラム原器は,多くの学者,技術者の苦心の末に,また,この合金の調製の技術を巡る仏英間の競合の逸話などを残しながら,1880年代の末に完成し,89年の第1回国際度量衡総会の承認のもとに各国へ配布され始めた。日本への配布は90年になされた。一方,新単位の値をもっとも忠実に具現すると判断される原器が選び出され,それらは国際メートル原器および国際キログラム原器の名のもとに,国際度量衡局の地下室に厳重に保管されることになった。ただしここで注意を要するのは,新単位の値のもっとも忠実な具現の内容であって,第1回総会の合意による判断基準は,〈アルシーブのメートルおよびアルシーブのキログラムで具現されていた値ともっともよく近似,または合致すること〉であった。こうして〈地球子午線の……〉および〈蒸留水の……〉との直接の結びつきは断たれることになった。言い換えれば,地球子午線の長さと一定体積・一定温度の蒸留水の質量とは,単位の具現者の任を解かれ,あらためて,国際原器に基づく新たな測定の対象と解釈し直されるに至ったのである。
それ以後,原器はまさにかけがえのない基準の物体として機能し続けてきた。そしてキログラム原器の場合,元来の機能が今なお持続されているが,他方のメートル原器の場合,かねての機能は1960年に廃止されて,メートルという単位の具現者はまったく別なものに移り,83年,さらに別なものに移ることになった。ただし,具現される1mという長さ自体は,事実上まったく変更されずに今日に及んでいる。
このような学術的な面での変遷と並行して,メートルを中核とする単位の制度,いわゆるメートル法système métriqueは,急速ではなかったにせよ着々と諸国に普及した。日本では1958年末を境としてほぼ全面的なメートル法専用が貫徹された。ヤード・ポンド系の単位は,いくつかの国で今も用いられているが,その実体は,59年以後,1ヤード=0.9144mなどの関係を介してメートル法の単位から誘導されることになった。
単位の体系
メートル法というときの〈法〉に対応する欧語はsystem,système,Systemなどであって,語義上では〈体系〉〈系統〉,または単に〈系〉と訳すほうがよい。単位に関しても,一つの系統を形づくるようにとりまとめられた一群の単位の体系を考えることがあり,そのような体系を一般に単位系system of unitsと呼んでいる。その際,どのような系統のもとに諸単位をとりまとめるかについては,いろいろな着眼点がありうるが,もっとも重要なのは,どのような量を,いくつ,基本的なものとして選ぶか,そして,それぞれに対してどのような単位をあてはめるかの2点である。
提案ないし実現されたさまざまな単位系のうち,現代社会と深くかかわるものについて概説しておく。基本的な量として,長さ,重さ(物体に作用する重力),時間の3者を選んだ単位系は,重力単位系,または工学単位系と呼ばれ,土木,水理その他の工学の諸分野で広く用いられてきているが,一つの(一定の質量をもつ)物体に作用する重力は場所と時によって変わるものであるから,重力を基本的な量として選ぶのは好ましくないと考えられるようになり,むしろ,長さ,質量,時間の3者を基本的な量として選んだ単位系(絶対単位系ともいう)が,より広く支持されることになった。
次に,長さ,質量,時間のそれぞれに対してどのような単位をあてはめるかが問題になる。メートル法の範囲でも,かつては,センチメートル(cm),グラム(g),秒(s)をあてはめた単位系(CGS単位系)が便利とされていたが,20世紀に入ってから,電磁気諸量の単位のこととも関連して,メートル(m),キログラム(kg),秒(s)をあてはめた単位系(MKS単位系)のほうがいっそう便利と認められることになった。
一方,19世紀後半以後の科学技術,とりわけ熱,光,電磁気,物性にかかわる諸学術の進歩は,単位系の議論にもさまざまなインパクトを与えた。なかでも電磁気については,静電気現象の記述に便利な静電単位系と電磁誘導現象の記述に便利な電磁単位系との二つがJ.C.マクスウェルによって提案されたのち,多種類の単位系が考え出されて今日に及んでいる。例えば,上記の三つの基本的な量のほかに第4,さらには第5のものを選ぶ必要があるとして,4元あるいは5元の単位系が提案されたし,電磁現象の法則を表す数式の中の幾何学的因子πをどう扱うかに応じて,有理系と非有理系とを区別することも必要となった。また,日常的な量の表現に適合するよう構成された実用単位系,国際間で協定した標準器を基礎として構成された一群の国際単位も,実社会では重要視された。
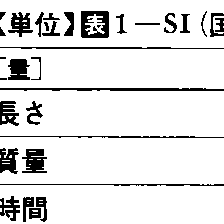
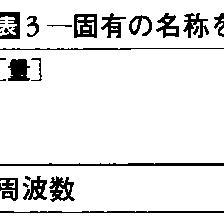
電磁気に関する単位系はこのように複雑化の傾向をたどったが,他の分野でも,多かれ少なかれ同様な傾向がみられた。すなわち,熱に関しては温度,熱量,エネルギーなどの単位,光に関しては波長,光度,光束,照度などの単位,物質の化学的性質に関してはいわゆる物質量の単位などが,それぞれ議論の対象となり,分野ごとにさまざまな単位や単位系が提唱されることにもなった。それらの大部分はメートル法の理念に沿うものであったから,拒否の対象とすることはできないが,一面,単位系の多様化は避けられなければならない。この矛盾は,1930年代からの検討の末に,60年の国際度量衡総会でひとまず解決され,国際単位系(SI)が成立した。国際単位系は,選ばれた七つの基本的な量(基本量)(長さ,質量,時間,電流,熱力学温度,物質量,光度)にそれぞれ対応させて基本単位(メートル,キログラム,秒,アンペア,ケルビン,モル,カンデラ)を定め,また,二つの補助的な量(平面角,立体角)に対応させて補助単位(ラジアン,ステラジアン)を定め,他の量については,物理学上の定義や法則を表す関係式の仲介のもとに〈組立量〉を考え,煩雑な係数などは用いないで簡明に〈組立単位〉を定めている。このような構成をもつ国際単位系は,既述の単位系一般論の立場でみれば,重力系でなく絶対系,CGS系でなくMKS系に属し,電磁気についていえば,静電系,電磁系のどちらでもないMKSA(Aはアンペア)系,非有理系でなく有理系のものといえ,全体として7元(補助単位を含めれば9元)の,一貫性のある(コヒーレントな)系を構成している。
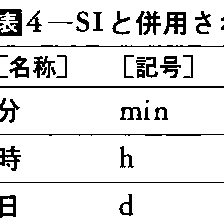
国際単位系は,全世界で使うことのできる単一の実用的な単位系として協定されたものであって,理論的にはなお改変の余地をもつかもしれないが,すでに世界主要国に普及し,その効用に強い期待が寄せられている。ただし現実には,国際単位系以外の単位のうち10個の併用,12個の暫定併用が認容されているなどの不徹底さも残っている。
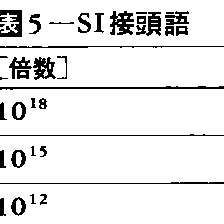
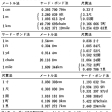
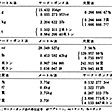
ともあれ,単位の世界にかつて認められた無秩序な多様化は,国際単位系の成立によって抑制されることになったといえよう。再び〈長さ〉の単位を例にとれば,建築用の曲尺,和裁用の鯨尺,麻布などのためのエレが復活されることはもはやないであろうし,ねじ用のインチも遠からず不要となるであろう。また,海上距離のための海里,光の波長のためのオングストローム,X線の波長のためのX線単位のような,特定分野で定められた単位も,しだいに顧みられなくなるであろう。これらの量は,すべて,幾何学的または物理的に〈長さ〉と解されるのであるから,おしなべて,国際単位系の単位メートルで,またはそれに所定の接頭語をつけて構成した単位キロメートル,センチメートル,ミリメートル,マイクロメートル,ナノメートルなどで表現すればよいのである。(表5)
日本の現今の単位は,計量の行政の面では計量法によって,また工業の面では工業標準化法に基づく日本工業規格JISによって,国際単位系への完全な整合化の方向へ段階的に改廃されつつある。
単位の現示と基礎物理定数
質量の単位は,前述のとおり国際キログラム原器によって具現され,それとの比較のなされている各国の原器がその国の質量測定の究極の基準の役をする。長さの単位も,かつては原器で具現されていたが,1920年代からの各国の研究の結果,60年の国際度量衡総会でメートル原器の機能の停止が宣言され,それ以後,メートルという単位は特定の光の波長に基づいて定義されることとなった。さらに83年の総会では,真空中での光の速さcに基づく定義への再変更が承認された。
1mという長さ自体は,〈アルシーブのメートル〉以来事実上まったく変えられずに今日に及んでいるのであるが,それを具現するものは,国際原器のような地球上ただ一つの物体から,原子スペクトル光源や安定化レーザーのような物理実験装置へと大きく変容した。物理学の進歩がもたらしたこの変容に伴って,単位の一定性は格段に確実なものとなり,一方,原器万能の権威主義は緩和され,相応の物理的な知識と技術をもつ人はだれでも単位を現示できるという事態が到来した。時間の単位の面では原子構造に関連する一定周波数の電磁波が,電磁気の単位の面ではジョセフソン効果という量子的現象が,それぞれ現代的な単位の現示手段として活用されている。これらの物理現象には,真空中の光速cのほかプランク定数hや電子の荷電eなどの基礎物理定数が直接に関与しているのであって,一定な物理的量という意味での単位と基礎物理定数とのかかわり合いを重視している点に,近年の単位論の特色が認められる。
→国際単位系 →度量衡
執筆者:高田 誠二
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「単位」の意味・わかりやすい解説
単位
たんい
unit 英語
unité フランス語
Einheit ドイツ語
物理量を計る場合の基準となる一定量。物理量とは、物や現象のうち、その性質が物理学的に明確で、その大きさを数量で表すことのできるものをいう。計量単位ともいう。物理量は、物理学の体系のなかで長さ、質量、時間などの基本的な量の含まれ方による「次元」dimensionが決まっている。次元とは、当該の量の座標軸に相当し、正負の符号が意味をもつ。たとえば速度vは単位時間T当りの長さLの変化であるから、
v=L/T=L1T-1
で、速度vはL1T-1の、またはLについて1、Tについて-1の次元ディメンションをもつという。また、面積は長さの2乗(L2)次元をもつ。物理量を計るということは、それと同じ量の一定量を約束して、計ろうとする量の大きさが約束した一定量の何倍であるかを数値で表すことである。この定義された一定量が単位で、量の大きさは、数値に単位をつけて表す。
物理量に対して、金属の硬さのように、物理的には量の定義が定まっていないが、計る方法や装置を約束して、その大きさを数値で表すものがある。この種の量で、工業上の必要から計るものを工業量という。
[小泉袈裟勝]
基本単位と組立単位
単位はどの量にも任意の大きさで約束できる。しかしある少数の、互いに独立な物理量に単位を選べば、ほかの量の単位はこれらを次元により組み合わせることによってつくることができる。この場合、最初に選ばれた単位を「基本単位」、組合せによってつくられた単位を「組立単位」または「誘導単位」という。たとえば、基本単位として長さにメートル(m)、質量にキログラム(kg)、時間に秒(s)をとれば、速度の単位は「メートル毎秒(m/s)」となり、力の単位は「キログラム・メートル毎秒毎秒(kg・m/s2)」となる。後者の場合長くなるので、これを「ニュートン(N)」と約束する。
[小泉袈裟勝]
単位の倍数と分数
基本単位と組立単位だけでは、大きさが適当でない場合が生ずるので、単位の倍数や分数の表し方を約束する必要がある。これにはさまざまな方法や習慣があるが、メートル法ではキロやセンチなどの接頭語を単位の頭につける方法をとっている。
[小泉袈裟勝]
単位記号
単位を逐一完全に書くのは煩わしいので、単位記号を約束する。メートル法は国際的な単位系であるから、この記号が厳密に定められている。通常は立体の小文字であるが、人名に由来するものは立体の大文字を用いる。たとえばメートルはm、キログラムはkg、ニュートンはNのようにする。しかし人名に由来するものでも単位名を完全に書くときは、たとえばnewtonと小文字で書く。また単位記号には、複数形はとらない。
[小泉袈裟勝]
単位系
基本単位を決め、それからいくつかの組立単位をつくると、ここに同族的な単位の系列ができる。これを単位系という。単位系の性格は基本単位のとり方で決まり、通常はこれを示すために基本単位あるいはその記号を並べてよぶが、そのほかの表し方もある。MKS単位系は基本単位に「メートル、キログラム、秒」を、CGS単位系は「センチメートル、グラム、秒」をとったものである。ヤード・ポンド法や尺貫法は、基本単位の名を連ねたものである。重力単位系は質量のかわりに地球重力加速度の下における力をとったものである。
単位系を特色づけるものに、もう一つ数値の進法がある。メートル法の十進(じっしん)法は18世紀末につくられたものであるが、それ以前の西洋の単位系は古代オリエントの六十進法や、ギリシア・ローマ時代の十二進法の混合したものである。
[小泉袈裟勝]
標準
単位は約束されても抽象的な数値だけでは意味がなく、その大きさを現実に示すもの、または方法がなくてはならない。これを標準standardという。とくに基本単位のそれは重要で、組立単位にも関係するから、第一に不変性と安定性、第二にいつでもどこでも実現できる性質つまり再現性、第三に十分高い精度が必要である。各種の単位系が基本的な量として長さ、質量および時間をとっているのは、これらが人類にとって基本的なもので、古くから標準の改良が行われてきているからである。
[小泉袈裟勝]
単位系の構成
少数の単位を基本単位とし、これを組み合わせて他の量の単位をつくるということは、すでに古代から行われていた。しかし、単位を定め、制度をつくらなければならない量は、長さ、面積、体積および質量に限られていた。そこでこのような体系や制度を度量衡、英語ではweights and measuresとよび、度のなかには面積を含み、measuresのなかには長さ、面積および体積を含ませている。時間は人類が計り始めた最初の量の一つと考えられるが、地球の自転周期という自然の標準があり、一昼夜の分割も太陽や星の位置に結び付ければよく、そこには1円周360度という自然の標準があった。そのため時間と角度とは度量衡以外の単位が実用されるようになるまで、単位系や制度のなかに組み込まれることはなかった。このような単位が必要になるのは、科学と工業がおこってからなので、ヤード・ポンド法とメートル法以外の単位系には含まれていない。ただ、地球の自転軸が公転軌道面に対して傾いているため、暦は別に定めるのが一般的であった。
[小泉袈裟勝]
単位系の種類
(1)尺貫法 尺と貫を基本単位とする日本固有の単位系。その起源は古代中国にあって共通する点は多いが、中国では質量に斤をとっている。
(2)ヤード・ポンド法 ヤードとポンドを基本単位にとったアングロ・サクソン系の単位系。工学用としてはこれに時間の秒が加わり、温度に華氏(かし)度(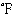 )をとる。起源は古代オリエントのもので、ギリシア、ローマおよびアラビア系の影響が加わっている。
)をとる。起源は古代オリエントのもので、ギリシア、ローマおよびアラビア系の影響が加わっている。
(3)メートル法 1790年、フランスのタレーランの提案により国際統一を目ざしてつくられた単位系で、国際的には1875年のメートル条約により発効した。「すべての時代に、すべての人々に」をスローガンとして、長さには地球子午線の4000万分の1を1メートルとした。
このようにつくられたメートル法も、度量衡以外の単位が科学や工業の必要から単位系に組み込まれるようになったとき、各種の単位系に分かれた。そのおもなものをあげると、MKS単位系、MKSA単位系、CGS単位系、CGS静電単位系、CGS電磁単位系、ガウスの絶対単位系、重力単位系などである。
(4)国際単位系 メートル法は、本来国際的統一単位系としてつくられたものであるから、前述のようにいくつかの単位系に分かれることははなはだ都合が悪い。そこで1960年の第11回国際度量衡総会において、これらを統一した単位系として決議されたのが国際単位系Système International d'Unitésである。SIという略称もこのときに決められた。
[小泉袈裟勝]
『小泉袈裟勝著『単位の起源事典』(1982・東京書籍)』▽『小泉袈裟勝著『単位のおはなし』(1979・日本規格協会)』▽『小泉袈裟勝著『続単位のおはなし』(1985・日本規格協会)』▽『『JISZ8202 量記号、単位記号及び化学記号』(1985・日本規格協会)』▽『『JISZ8203 国際単位系(SI)及びその使い方』(1985・日本規格協会)』
百科事典マイペディア 「単位」の意味・わかりやすい解説
単位【たんい】
→関連項目測定
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「単位」の意味・わかりやすい解説
単位
たんい
unit
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
普及版 字通 「単位」の読み・字形・画数・意味
【単位】たんい
字通「単」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
関連語をあわせて調べる
目次 飼養文化 北アメリカ 北方ユーラシア偶蹄目シカ科の哺乳類。北アメリカでは野生種はカリブーcaribouと呼ばれる。角が雄だけでなく雌にもふつうある。体長130~220cm,尾長7~20cm,...