翻訳|convergence
精選版 日本国語大辞典 「収束」の意味・読み・例文・類語
しゅう‐そくシウ‥【収束】
- 〘 名詞 〙
- ① 集めてたばねること。また、その状態。
- [初出の実例]「漏斗状の斜面の収束するところに木が生え」(出典:野火(1951)〈大岡昇平〉八)
- ② おさまりのつくこと。決着がつくこと。
- [初出の実例]「云ふ事は散漫であった。〈略〉収束(シウソク)する所なく〈略〉仕舞に飽きた」(出典:道草(1915)〈夏目漱石〉九六)
- ③ 数学で、関数、数列、級数に関して用いる語。
- (イ) 関数の値がある値に限りなく近づくこと。関数 f(x) において、xがaに近づくとき f(x) が値bに限りなく近づくならば、関数 f(x) は、xがaに近づくときbに収束するという。
- (ロ) 数列の項がある値bに限りなく近づくこと。このとき、その数列はbに収束するという。
- (ハ) 級数 a1+a2+a3+… の途中までの和がある値bに限りなく近づくこと。このとき、その級数はbに収束するという。収斂。
- ④ 光線などの束が一点に集中すること。また、その状態。集束。収斂。
- ⑤ 将棋で、寄せのこと。
日本大百科全書(ニッポニカ) 「収束」の意味・わかりやすい解説
収束
しゅうそく
convergence
ある値に限りなく近づくことを表す数学用語。以前は収斂(しゅうれん)ともいった。
数列の収束
数列a1, a2,……, an,……において、添数のnが限りなく大きくなるとき、anの値がある値Aに限りなく近づくならば、anはAに収束するという。Aをこの数列の極限値とよび、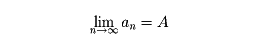
と書く。収束しない数列は発散するという。数列の収束を論ずる際に基礎となるのは次の定理である。
(1)単調増加。有界な数列は、ある極限値に収束する。すなわち、a1≦a2≦‥‥‥であり(単調増加)、かつある定数Mがあって、すべてのnについてan≦M(上に有界)であるならば、ある値Aがあって、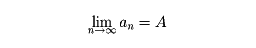
となる。
(2)数列が基本列ならば収束する。基本列というのは、先のほうに行くにしたがってお互いどうしの差の絶対値がいくらでも小さくなるような数列のことである。
[竹之内脩]
関数値の収束
一つの実変数の関数f(x)を考える。この関数がx=aの近くで定義されているとする(x=aでは定義されていてもいなくてもよい)。ある一定の数Aがあって、aに収束し、かつaと異なる数列x1, x2,……を任意にとったとき、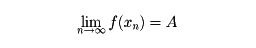
となるならば、これを「xがaに近づくとき、f(x)はAに収束する」といい、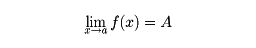
で表し、Aを、xがaに近づくときの極限値という。さらにx<aでありながらxがaに近づくときの極限値が定義される。これを左側極限値といって、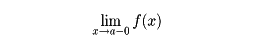
あるいはf(a-0)で表す。同様に右側極限値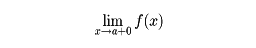
あるいはf(a+0)が定められる。f(x)がx→aのときの極限値を有するための一つの条件はf(a-0), f(a+0)がともに存在して相等しいことである。
以上は1変数の関数の場合であったが、同様のことは変数の数が多い場合(多変数関数)についてもいえるし、関数の値が高次元空間の点の場合(写像または変換)にも適用される。
[竹之内脩]
関数列の収束
ある集合Dの上で定義された関数の列f1(x), f2(x),……があるとき、Dの任意の要素xに対して、数列f1(x), f2(x),……がつねに収束するならば、その極限値をxに対応させて一つの関数f(x)が得られる。この関数を極限関数といい、このとき、関数列f1(x), f2(x),……はf(x)に収束(あるいは、詳しくは各点収束)するといって、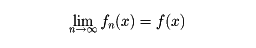
で表す。関数列が各点収束するだけでは、極限関数の性質を十分に得ることができない。関数列の収束の議論には、一様収束および平均収束の概念が重要である。
[竹之内脩]
εδ論法
以上述べてきたことは、収束についての概念的な論じ方であって、数学的に十分に精密な議論ではない。厳密には、収束を次のように定義して論じる。「数列a1, a2,……について、ある数Aがあって、どのようなε>0に対しても、自然数Nを適当にとれば、n≧Nであるようなすべての自然数nに対して、|an-A|≦εが成り立つとき、anはAに収束するという」。また、数列a1, a2,……について、どのようなε>0に対しても、自然数Nを適当にとれば、n, m≧Nであるようなすべての自然数n、mに対して、|an-am|≦εが成り立つとき、この数列を基本列あるいはコーシー列という。数列a1, a2,……がある数Aに収束するための必要十分条件は、それが基本列であることである。次に、x=aの近くで定義された関数f(x)に対して、ある数Aがあって、どのようなε>0に対しても、適当にδ>0をとれば、|x-a|≦δ, x≠aであるようなすべてのxに対して、|f(x)-A|≦εが成り立つとき、f(x)はAに収束するという。これは先に与えた定義と非常に異なるが、内容は同じことになる。収束についてのこのような形の厳密な論理展開は、17世紀イギリスの数学者ウォリスが初めてだといわれている。一般に用いられるようになったのは、19世紀中ごろからである。日本の数学教育のなかでは、大学の数学で初めて登場する。εとδを用いて論じられることが多いのでεδ論法(イプシロンデルタろんぽう)という。
[竹之内脩]
改訂新版 世界大百科事典 「収束」の意味・わかりやすい解説
収束 (しゅうそく)
convergence
(1)数列の収束 実数または複素数を項とする無限数列{an}(n=1,2,……)があって,項の番号nが限りなく増していくとき,対応する項anが一つの数αに限りなく近づく場合に,この数列は収束して極限値αをもつ,またはαに収束するといい,このことを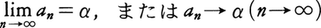 で表す。例えば
で表す。例えば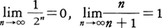 (2)点列の収束 距離ρが定義されている空間に,無限点列{pn}(n=1,2,……)があるとする。その空間に1点pがあって,距離の数列{ρ(pn,p)|n=1,2,……}が0に収束するとき,点列{pn}は距離ρに関して点pに収束するといい,点pを点列{pn}の極限点という。このことを
(2)点列の収束 距離ρが定義されている空間に,無限点列{pn}(n=1,2,……)があるとする。その空間に1点pがあって,距離の数列{ρ(pn,p)|n=1,2,……}が0に収束するとき,点列{pn}は距離ρに関して点pに収束するといい,点pを点列{pn}の極限点という。このことを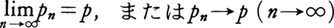 で表す。例えば,平面上で点pnの座標を(xn,yn)とするとき,
で表す。例えば,平面上で点pnの座標を(xn,yn)とするとき,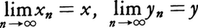 ならば点列{pn}は座標(x,y)をもつ点pに収束する。実数または複素数はそれぞれ直線または平面上の点と対応させられるから,実数列または複素数列の収束は,ふつうの意味での距離に関する点列の収束の特別な場合とみなされる。
ならば点列{pn}は座標(x,y)をもつ点pに収束する。実数または複素数はそれぞれ直線または平面上の点と対応させられるから,実数列または複素数列の収束は,ふつうの意味での距離に関する点列の収束の特別な場合とみなされる。
(3)関数の収束 距離空間(一般に位相空間)の中の集合Eで定義された実数,または複素数値関数f(p)があり,また点qがEの集積点(Eの中に,qを含まない点列で,qに収束するものがとれる)とする。点pがEの中を通って(qに一致することなく)qに限りなく近づくとき,f(p)が一つの値αに限りなく近づく場合に,p→qのときf(p)は極限値αをもつ,またはαに収束するといい,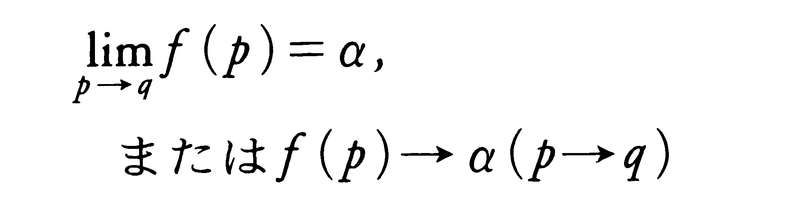
と書く。例えば,実数x≠0で定義された関数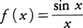 については
については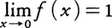
数列の特別な形としての無限級数の収束については,〈級数〉の項目を参照されたい。
(4)レンズや鏡などの作用で,光が一点に集まること,あるいは流体や電流が吸込みに向かって運動することをいう。
→発散
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「収束」の意味・わかりやすい解説
収束
しゅうそく
convergence
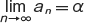 あるいは an→α(n→∞) と書く。数列 {an} が与えられたとき,Sn=a1+a2+…+an(n=1,2,…) とおき,ここから新しい数列 {Sn} をつくった場合に,この数列が収束して有限な極限値 S をもてば,無限級数 a1+a2+…+an+… は収束するといい,このときの極限値 S を,無限級数の和という。これを
あるいは an→α(n→∞) と書く。数列 {an} が与えられたとき,Sn=a1+a2+…+an(n=1,2,…) とおき,ここから新しい数列 {Sn} をつくった場合に,この数列が収束して有限な極限値 S をもてば,無限級数 a1+a2+…+an+… は収束するといい,このときの極限値 S を,無限級数の和という。これを 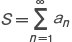 と書く。数列の収束を拡張して,関数の収束を定義することができる。関数 y=f(x) が 0<|x-a|<r で定義されているとき,一定の実数αがあって,任意の正の数 ε に対し適当に δ<r を定めて,0<|x-a|<δ ならば必ず |f(x)-α|<ε となるようにできるとき,f(x) はαに収束する。あるいは f(x) は x=a において極限値αをもつという。この場合の δ は ε に対して定まる値である。記号では
と書く。数列の収束を拡張して,関数の収束を定義することができる。関数 y=f(x) が 0<|x-a|<r で定義されているとき,一定の実数αがあって,任意の正の数 ε に対し適当に δ<r を定めて,0<|x-a|<δ ならば必ず |f(x)-α|<ε となるようにできるとき,f(x) はαに収束する。あるいは f(x) は x=a において極限値αをもつという。この場合の δ は ε に対して定まる値である。記号では 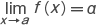 または f(x)→α(x→a) と書き表わす。ただし,最近では,x=a すなわち |x-a|=0 を含めて,条件の 0<|x-a| の部分を省く流儀もある。
または f(x)→α(x→a) と書き表わす。ただし,最近では,x=a すなわち |x-a|=0 を含めて,条件の 0<|x-a| の部分を省く流儀もある。
収束[気流]
しゅうそく[きりゅう]
convergence
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「収束」の意味・わかりやすい解説
収束(数学)【しゅうそく】
→関連項目級数|グレゴリー|収斂|数列|無限級数
収束(物理)【しゅうそく】
→関連項目沈降流|レンズ
出典 株式会社平凡社百科事典マイペディアについて 情報
最新 地学事典 「収束」の解説
しゅうそく
収束
conversion
⇒ プレート境界
出典 平凡社「最新 地学事典」最新 地学事典について 情報
普及版 字通 「収束」の読み・字形・画数・意味
【収束】しゆうそく
字通「収」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
世界大百科事典(旧版)内の収束の言及
【眼筋】より
…これに対し,運動方向と逆の作用をもつ筋群(上記の場合は右眼の内直筋と左眼の外直筋)を拮抗筋という。眼球の非共同運動には輻輳(ふくそう)convergence(収斂(しゆうれん)ともいう)と開散divergence(発散ともいう)の2型がある。輻輳は眼前の一点に視線を集中させる機能で,ふつう両眼の内直筋の収縮によって行われる。…
【収れん(収斂)】より
…系統の異なる生物分類群の間で独立に器官の形や体全体の形が類似する方向に進化することをいう。収れんの結果生ずる生物間の形態の見かけの類似現象をホメオモルフィーhomeomorphyといい,さまざまのレベルの分類群の間で認められる。多くは生態(特に運動様式・食性)の類似に関連して起こる。例えば,軟骨魚類のサメ,中生代に栄えた爬虫類の魚竜,哺乳類のイルカは骨格の基本的構造は著しく異なるが,いずれも遊泳に適した流線型の体形をもつ。…
【目∥眼】より
…外眼筋は一つの目に六つあり,それらの筋肉の働きで,眼球は水平,上下,斜めの方向へ動く。両目の視線を目前の1点に集中させる働きが輻湊(ふくそう)convergenceである。近いところを見るときには輻湊とともに調節が起こる。…
【級数】より
…snが簡単な式で表される級数の例として,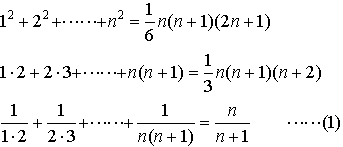 などがある。また〈等差数列〉 〈等比数列〉の項目にも述べられているように,
などがある。また〈等差数列〉 〈等比数列〉の項目にも述べられているように,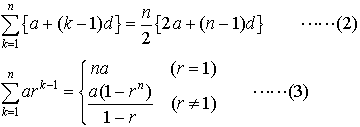 与えられた級数の部分和の数列{sn}において,nが限りなく大きくなるときsnがある定まった値sに限りなく近づくならば,すなわち数列{sn}が極限値sをもつならば,その級数は収束して和sをもつ,またはsに収束するといい,このことを
与えられた級数の部分和の数列{sn}において,nが限りなく大きくなるときsnがある定まった値sに限りなく近づくならば,すなわち数列{sn}が極限値sをもつならば,その級数は収束して和sをもつ,またはsに収束するといい,このことを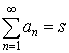 と書く。それ以外の場合には級数は発散するという。…
と書く。それ以外の場合には級数は発散するという。…
【極限】より
…数列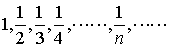 を考えると,この数列の第n項は,nが限りなく大きくなるにつれて0に限りなく近づく。一般に一つの無限数列{an|n=1,2,……}の第n項anが,nを限りなく大きくするときある一定の数Aに限りなく近づくとき,この数列は収束するといい,Aをこの数列の極限値と呼ぶ。記号で,
を考えると,この数列の第n項は,nが限りなく大きくなるにつれて0に限りなく近づく。一般に一つの無限数列{an|n=1,2,……}の第n項anが,nを限りなく大きくするときある一定の数Aに限りなく近づくとき,この数列は収束するといい,Aをこの数列の極限値と呼ぶ。記号で,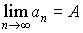 で表す。…
で表す。…
【発散】より
…数列の発散とベクトル場の発散の二つがある。
[数列の発散]
無限数列{xn}が収束しないとき,この数列は発散するという。とくに実数列{xn}において,nを限りなく大きくするときxnが限りなく大きくなるならば{xn}は正の無限大に定発散するといって,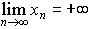 と書き,nを限りなく大きくするときxnが負になってその絶対値が限りなく大きくなるならば{xn}は負の無限大に定発散するといって,
と書き,nを限りなく大きくするときxnが負になってその絶対値が限りなく大きくなるならば{xn}は負の無限大に定発散するといって,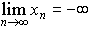 と書く。…
と書く。…
※「収束」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


