デジタル大辞泉
「像」の意味・読み・例文・類語
出典 小学館デジタル大辞泉について 情報 | 凡例
Sponserd by 
ぞうザウ【像】
- 〘 名詞 〙
- ① 物の形。人のすがた。また、神・仏・人・獣などの形をまねて作ったり描いたりしたもの。
- [初出の実例]「昔の国王のつくれる観音の像あり」(出典:観智院本三宝絵(984)中)
- [その他の文献]〔水経注〕
- ② 「ぞうぼう(像法)」の略。
- [初出の実例]「秀句に云く、代を語れば則像の終り末の初め、地を尋れば則唐の東羯の西」(出典:日蓮遺文‐開目抄(1272))
- ③ 物体から出た光が、レンズや鏡によって屈折または反射した結果、光線が集合して物体と相似の形を形成したもの。実際に集合してつくる像を実像という。また、レンズや鏡を通過または反射した光が、実際には集合しないが、あたかもある像から発したように進む場合、この光を目に受けると、その像のところに物体が存在するように見えるのを虚像という。〔物理学術語和英仏独対訳字書(1888)〕
- ④ 数学で、写像によって元または集合に対応する元または集合。fが集合Aから集合Bへの写像のとき、fによってAの元aに対応するBの元bを、fによるaの像といい、f(a) で表わす。また、Aの部分集合Mの元のfによる像の全体を、fによるMの像といい、f(M) と書く。
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報 | 凡例
Sponserd by 
普及版 字通
「像」の読み・字形・画数・意味
出典 平凡社「普及版 字通」普及版 字通について 情報
Sponserd by 
像 (ぞう)
image
物体の1点から出た光線束が光学系による反射と屈折を経た後,再び1点で交わるとき,光線束の出る物体の1点を物点,再び交わる1点を像点といい,像点の集まったものを像と呼ぶ。光学系を通過した光線束が実際に1点に集まる場合を実像real image,光線を逆向きに延長したときに1点で交わる場合を虚像virtual imageという。例えば凸レンズによる太陽の像は実像であるが,姿見に映った像は虚像である。実像の位置に感光材料をおけば像を記録できるが,虚像では不可能である。また像で,物体と上下左右の配列が同じものを正立像,反対のものを倒立像という。光学系の性質および物体の位置により,像の実,虚,正立,倒立が決まる。
共軸球面光学系では,光軸に垂直な面内の物点は,近軸光線による結像の場合,同じく光軸に垂直な面内に結像し,物体と像とは相似である。しかし実際の光学系においては,像面の湾曲や歪曲の収差のために像は物体の忠実な模写でなくなり,また上記以外の収差により光線束が1点に集まらず,その結果像は不鮮明になる。
点光源の像を点像というが,これは収差および開口絞りによる回折のため有限な広がりをもつ。すなわち,実際の光学系では,一つの物点に対して,広がりのある像が対応する。幾何光学的に求めた点像はスポットダイヤグラムと呼ばれ,写真レンズのような,残存収差が大きい場合の結像評価に用いられる。しかし,点像を厳密に求めるには収差の項を含む回折積分を解く必要がある。
→鏡 →球面鏡 →レンズ
執筆者:鶴田 匡夫
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
像
ぞう
image
数学用語。集合 X のおのおのの元 x に集合 Y の1つずつの元 y を対応させる写像を f:X→Y とする ( X から Y の上への写像) 。 f によって X の元 x に対応する Y の元 f(x) を,f による x の像という。さらに X の部分集合 S のすべての元の像の集合を f(S) と書き,これを f による S の像という。 f(S) は Y の部分集合である。たとえば実数の集合 R から R の上への写像が y=f(x)=x2+1 で与えられているとき,R の像は y≧1 を満足する実数 y の集合である。特に f(x) のことを単に f の像という。
像
ぞう
image
光学用語。1点から出た光線束がレンズや曲面鏡を通ったのち,再び1点に集るとき,その後者の点 (像点) を前者の点 (物点) の像という。光線は逆に進めば,完全にもとの道をたどるので,像点と物点とは互いに共役である。光線が実際に像を通る場合にその像を実像,実際には通らないが光線を逆に延長したとき像点に集る場合にその像を虚像という。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内の像の言及
【写像】より
…2変数の関数f(x,y)は,平面の点(x,y)に,関数の値f(x,y)を,それぞれ定めていると考えられる。この考えを一般にしたものが写像である。つまり,集合Aの各元に,集合Bの元を,ある規則によりそれぞれ定めているとき,この規則をAからBへの写像という。…
※「像」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 



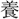 字の
字の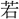 (ごと)くす」という。〔楚辞、九章、懐沙〕「志の像(のり)
(ごと)くす」という。〔楚辞、九章、懐沙〕「志の像(のり)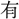 らんことを願ふ」、〔九章、橘頌〕「置きて以て像と爲さん」のように、〔楚辞〕に用例が多い。
らんことを願ふ」、〔九章、橘頌〕「置きて以て像と爲さん」のように、〔楚辞〕に用例が多い。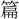 立〕像 イタル・ニタリ・ヤル・カタチ・カタドル・カタシロ・ウツス・オモヒヤル
立〕像 イタル・ニタリ・ヤル・カタチ・カタドル・カタシロ・ウツス・オモヒヤル 像・虚像・胸像・玉像・偶像・群像・形像・幻像・現像・骨像・坐像・座像・残像・実像・寿像・肖像・心像・神像・図像・聖像・石像・塑像・想像・尊像・雕像・泥像・銅像・仏像・木像・立像・霊像
像・虚像・胸像・玉像・偶像・群像・形像・幻像・現像・骨像・坐像・座像・残像・実像・寿像・肖像・心像・神像・図像・聖像・石像・塑像・想像・尊像・雕像・泥像・銅像・仏像・木像・立像・霊像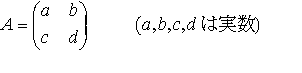 を一つ取り,平面のベクトル,
を一つ取り,平面のベクトル,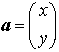 に対して,
に対して,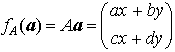 と定める。fA(a)もまた平面のベクトルになるから,fAは平面のベクトル全体の集合からそれ自身への写像である。ところで,任意のベクトルa,bと,任意のスカラーα,βについて,fA(αa+βb)=αfA(a)+βfA(b)となる。…
と定める。fA(a)もまた平面のベクトルになるから,fAは平面のベクトル全体の集合からそれ自身への写像である。ところで,任意のベクトルa,bと,任意のスカラーα,βについて,fA(αa+βb)=αfA(a)+βfA(b)となる。…