翻訳|sphere
精選版 日本国語大辞典 「球」の意味・読み・例文・類語
きゅうキウ【球】
- 〘 名詞 〙
- ① まりのように丸いもの。たま。「電球」「地球」
- ② 空間における、一定点から等距離にある点全体から成る曲面(球面)、あるいはそれによって囲まれた立体(球体)。〔医語類聚(1872)〕
- [初出の実例]「太陽は、大なる球にて、世界に、光と熱を与ふ」(出典:小学読本(1873)〈田中義廉〉二)
普及版 字通 「球」の読み・字形・画数・意味
15画
(異体字)球
11画
[字訓] たま
[説文解字]


[字形] 形声
声符は
 (りょう)。
(りょう)。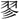 に
に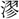 (こう)・樛(きゅう)の声がある。〔説文〕一上に球を正字とし、「玉聲なり」といい、重文として
(こう)・樛(きゅう)の声がある。〔説文〕一上に球を正字とし、「玉聲なり」といい、重文として を録する。〔爾雅、釈器〕に「
を録する。〔爾雅、釈器〕に「 琳は玉なり」、〔爾雅、釈地〕に「西北の美なる者」として崑崙(こんろん)虚の
琳は玉なり」、〔爾雅、釈地〕に「西北の美なる者」として崑崙(こんろん)虚の 琳・琅
琳・琅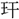 (ろうかん)をあげている。玉磬(ぎょくけい)の鳴るのを
(ろうかん)をあげている。玉磬(ぎょくけい)の鳴るのを 然・
然・ 鏘(きうさう)のように形容するが、球にはその用義法がなく、両字の間に慣用を異にするところがある。
鏘(きうさう)のように形容するが、球にはその用義法がなく、両字の間に慣用を異にするところがある。[訓義]
1. 美しい玉、
 琳。
琳。2. 玉磬。
3. 玉声。
[古辞書の訓]
〔名義抄〕
 タマ 〔
タマ 〔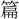 立〕
立〕 タマノナナリ・テハツクリ
タマノナナリ・テハツクリ[語系]
 はまた球に作る。求giu、
はまた球に作る。求giu、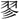 liu、九kiu、
liu、九kiu、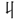 kyuは声義に通ずるところがあり、その形声字に糾纏・宛曲の義を含むことが多い。
kyuは声義に通ずるところがあり、その形声字に糾纏・宛曲の義を含むことが多い。[熟語]
 磬▶・
磬▶・ 然▶・
然▶・ 鏘▶・
鏘▶・ 鉄▶・
鉄▶・
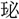 ▶・
▶・ 林▶・
林▶・ 琳▶
琳▶[下接語]
素
 ・大
・大 ・白
・白 ・
・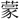
 ・琳
・琳
球
常用漢字 11画
(異体字)
15画
[字訓] たま
[説文解字]


[字形] 形声
声符は求(きゆう)。求は裘の初文。求にまるくして巻きこむ意がある。〔説文〕一上に「玉なり」(段注本)とし、重文として
 の字形をあげている。〔書、益稷〕に「
の字形をあげている。〔書、益稷〕に「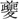 (き)(楽祖とされる神名)曰く、戛(かつ)として鳴球を
(き)(楽祖とされる神名)曰く、戛(かつ)として鳴球を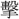 つ」、また〔楚辞、九歌、東皇太一〕に「長劍の玉珥を撫すれば
つ」、また〔楚辞、九歌、東皇太一〕に「長劍の玉珥を撫すれば  鏘(きうさう)として琳琅(りんらう)鳴る」とあって、いずれも玉声をいう。求・
鏘(きうさう)として琳琅(りんらう)鳴る」とあって、いずれも玉声をいう。求・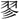 に、もと、まるい、糾纏(きゆうてん)するものの意があり、
に、もと、まるい、糾纏(きゆうてん)するものの意があり、 はまた美玉の名に用いる。
はまた美玉の名に用いる。[訓義]
1. たま、美しいたま。
2. 玉声。
3. 鳴球は玉磬。
[古辞書の訓]
〔名義抄〕球琳 上は玉磬、下は玉名なり 〔
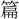 立〕球 タマノオト・タマ・コヱタマ
立〕球 タマノオト・タマ・コヱタマ[語系]
球・
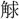 (
(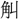 )・
)・ gyu、
gyu、 kyu、九kiuは声近く、その声符の字にみな、まるく巻きこむ意がある。
kyu、九kiuは声近く、その声符の字にみな、まるく巻きこむ意がある。[熟語]
球技▶・球球▶・球玉▶・球形▶・球状▶・球場▶・球灯▶・球拍▶・球琳▶
[下接語]
眼球・気球・血球・蹴球・小球・鏘球・打球・大球・卓球・地球・庭球・天球・投球・排球・鳴球・野球・籠球
出典 平凡社「普及版 字通」普及版 字通について 情報
改訂新版 世界大百科事典 「球」の意味・わかりやすい解説
球 (きゅう)
sphere
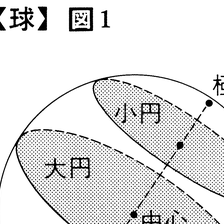
空間において,1定点から一定の距離にある点の全体を球面または球といい,定点をその中心という。中心と球面の点を結ぶ線分またはその長さを半径といい,球面の2点を結ぶ線分が中心を通るとき,この線分またはその長さを直径という。中心からの距離が半径より小さい点の全体を球面の内部,大きい点の全体を球面の外部という。球面とその内部を合わせたものも球と呼ばれる。球面を平面で切れば切口は円となる。この円を平面が中心を通るときには大円といい,そうでないときには小円という。大円の半径は球の半径に等しく,小円の半径は球の半径より小さい。大円の平面に垂直な球の直径を大円の軸といい,その両端の2点を大円の極という。球の直径の両端の2点を対心点という。球面の2点A,Bを通る大円は,A,Bが対心点でなければただ一つ定まり,A,Bが対心点ならば無数にある。球面の2点A,Bを結ぶ球面上の曲線のうち最小の長さをもつものはA,Bを通る大円の(劣)弧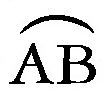 で,この長さをAとBの球面距離という。半径がrの球面の面積は4πr2で,その球の体積は4/3πr3である。表面積が与えられた立体の中で最大の体積をもつものは球である。球面または球は中心を通る平面によって互いに対称な二つの部分に分けられる。その各部分を半球面または半球という。球が平面と交わるとき,この平面の一方の側にある球面の部分は球冠と呼ばれ,球冠とこの平面で囲まれた立体は球欠と呼ばれることがある。球面が二つの平行な平面に交わるとき,これら2平面にはさまれた球面の部分を球帯といい,球帯とこれらの2平面で囲まれた立体を球台という。直線または平面が球面とただ1点を共有するとき,それらは球面に接するといい,共有点を接点という。この場合,直線を球の接線,平面を球の接平面という。接線や接平面は接点を通る半径に垂直である。二つの球面がただ1点を共有するとき,それらは接するといい,共有点を接点という。この場合,一方の球面の点が接点を除いて他方の球面の内部にあるか外部にあるかに応じて,これら2球は内接または外接するという。2球が接するとき,2球の中心を結ぶ直線上に接点がある。空間に直交座標を導入すれば,中心が(a,b,c)で半径がrである球面は,(x-a)2+(y-b)2+(z-c)2=r2を満たす点(x,y,z)の全体である。これを一般化して,n+1次元ユークリッド空間Rn⁺1の1点(a1,a2,……,an+1)と正数rに対し,Rn⁺1の点(x1,x2,……,xn+1)で(x1-a1)2+(x2-a2)2+……+(xn+1-an+1)2=r2を満たすものの全体をn次元球面という。二次元球面はふつうの球面で,一次元球面は円周,0次元球面は2点{+1,-1}である。
で,この長さをAとBの球面距離という。半径がrの球面の面積は4πr2で,その球の体積は4/3πr3である。表面積が与えられた立体の中で最大の体積をもつものは球である。球面または球は中心を通る平面によって互いに対称な二つの部分に分けられる。その各部分を半球面または半球という。球が平面と交わるとき,この平面の一方の側にある球面の部分は球冠と呼ばれ,球冠とこの平面で囲まれた立体は球欠と呼ばれることがある。球面が二つの平行な平面に交わるとき,これら2平面にはさまれた球面の部分を球帯といい,球帯とこれらの2平面で囲まれた立体を球台という。直線または平面が球面とただ1点を共有するとき,それらは球面に接するといい,共有点を接点という。この場合,直線を球の接線,平面を球の接平面という。接線や接平面は接点を通る半径に垂直である。二つの球面がただ1点を共有するとき,それらは接するといい,共有点を接点という。この場合,一方の球面の点が接点を除いて他方の球面の内部にあるか外部にあるかに応じて,これら2球は内接または外接するという。2球が接するとき,2球の中心を結ぶ直線上に接点がある。空間に直交座標を導入すれば,中心が(a,b,c)で半径がrである球面は,(x-a)2+(y-b)2+(z-c)2=r2を満たす点(x,y,z)の全体である。これを一般化して,n+1次元ユークリッド空間Rn⁺1の1点(a1,a2,……,an+1)と正数rに対し,Rn⁺1の点(x1,x2,……,xn+1)で(x1-a1)2+(x2-a2)2+……+(xn+1-an+1)2=r2を満たすものの全体をn次元球面という。二次元球面はふつうの球面で,一次元球面は円周,0次元球面は2点{+1,-1}である。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「球」の意味・わかりやすい解説
球
きゅう
sphere
空間において1点から一定の距離にある点全体の集合を球または球面といい、球によって囲まれる立体を球体という。点Aからの距離がrである点全体の集合として得られる球に対して、Aをその中心、rをその半径という。球の中心を通る直線と球とが交わる2点を対心点(または直径対点)といい、対心点を両端とする線分(またはその長さ、すなわち半径の2倍)をその球の直径という。球の中心を通る平面と球との交線を、その球の大円といい、中心を通らない平面と球との交線を小円という。球上の2点を結ぶ最短線は大円の一部である。
(x, y, z)を直交座標とするとき、中心が(a, b, c)で半径がrの球の方程式は
(x-a)2+(y-b)2+(z-c)2=r2
であり、この球によって囲まれる球体は不等式
(x-a)2+(y-b)2+(z-c)2≦r2
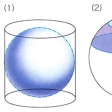
を満たす。半径rの球の表面積は4πr2であり、半径rの球体の体積は(4/3)πr3である。半径rの球の表面積はそれに外接する直円柱の側面積に等しい(の(1))。また半径rの球から間隔dの平行平面で切り取られる部分(の(2))の面積は2πrdである(平行平面の位置に関係なくその間隔だけで決まる)。
なお、小学校の教科書には「どこから見ても丸く見える図形を球という」と書かれている。これを厳密に述べれば「曲面S上にない任意の点Pについて、PとS上の点とを結ぶ直線全体の集合がPを頂点とする円錐(えんすい)をなすときSを球という」となる。これが球の自然な定義である。これに対して「空間において1点から一定の距離にある点全体の集合を球という」は論理的な定義である。この二つの定義は同値であるが、その証明はやさしくはない。
[荻上紘一]
ブリタニカ国際大百科事典 小項目事典 「球」の意味・わかりやすい解説
球
きゅう
sphere
(x-a)2+(y-b)2+(z-c)2=r2……(1)
で与えられる。中心Cが原点にある場合は,Cの座標は (0,0,0) であるから,方程式は
x2+y2+z2=r2……(2)
である。また次の不等式
(x-a)2+(y-b)2+(z-c)2≦r2……(3)
を満足する点全体を球ということもある。このときは,(1) を満たす点 ( x ,y ,z ) の全体を球面といい,(3) を球体という。球の表面積 S およびそれで囲まれる球体の体積 V は,それぞれ S=4πr2 ,V=4πr3/3 で与えられる。ただし r は半径,πは円周率である。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「球」の意味・わかりやすい解説
球【きゅう】
→関連項目半径
出典 株式会社平凡社百科事典マイペディアについて 情報
岩石学辞典 「球」の解説
世界大百科事典(旧版)内の球の言及
【延髄】より
…延髄という名称は本来,脊髄の延長を意味するところからきている。また延髄は球根のように膨らんでいるところから球という名称が用いられることがある。延髄の下方は脊髄最上端(第1頸神経の上縁)を境とする。…
※「球」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
[名](スル)1 人から受けた礼・贈り物に対して行為や品物で報いること。また、その行為や品物。「地酒を贈って返礼する」2 仕返しをすること。また、その仕返し。意趣返し。返報。[補説]書名別項。→返礼[...