翻訳|spin
精選版 日本国語大辞典 「スピン」の意味・読み・例文・類語
スピン
- 〘 名詞 〙 ( [英語] spin )
- ① 回ること。回転。旋回。「車がスピンする」 〔世界の自動車(1958)〕
- ② 飛行機の錐揉(きりもみ)降下。
- [初出の実例]「今日は錐揉み(スピン)の練習でしたね」(出典:汚れた英雄 雌伏篇(1968)〈大藪春彦〉大空の翼)
- ③ フィギュアスケートで、氷上の一点でこまのように、体を旋回させること。
- [初出の実例]「後の足を水平以上に高くあげながら、水鳥のやうに辷っては、姿勢をスピンに変へてゐた」(出典:臈たき花(1933)〈中河与一〉一二)
- ④ テニスや卓球などで、球に回転を与えること。また、その回転。
- ⑤ ダンスで、足の親指のつけ根のふくらんだ部分で回転すること。
- [初出の実例]「スピンは柔道の感じだった。〈略〉技をはずされて引きずり回されているような感じだった」(出典:金色の鼻(1973)〈古山高麗雄〉)
- ⑥ 糸をつむぐこと。
- ⑦ 電子または他の素粒子の自転運動に伴う角運動量のこと。その粒子固有の値をもつ。〔自然科学的世界像(1938)〕
日本大百科全書(ニッポニカ) 「スピン」の意味・わかりやすい解説
スピン
すぴん
spin
素粒子またはその複合粒子のもつ固有の角運動量で量子論的な自由度である。古典物理的な描像では粒子の自転による角運動量と考えられる。運動する粒子の全角運動量は、軌道角運動量とこのスピン角運動量のベクトル和で表される。
原子スペクトルの多重項構造、すなわち原子のエネルギー準位の微細構造の特徴を理解するために、パウリは、原子の軌道を運動する電子に新しく二価性をもつ自由度を付加した。クローニッヒRalph Kronig(1904―1995)、ハウトスミット、ウーレンベックは、パウリの前記の考えを粒子の自転と解釈し、自転に基づく角運動量の大きさが、ħ(ディラック定数。プランク定数hを2πで割ったもので、エイチ・バーと読む)を単位にして1/2の値をとると考えた(第3軸成分は±1/2の値をとる)。また電荷をもつものが回転していれば円電流が生じ、それに比例する磁気モーメントが予想できる。この磁気モーメントの、ボーア磁子eħ/2mc(eは電子の電荷、mは同じく質量、cは光速度)を単位にして測った値をμとして、このμとħを単位として測った角運動量との比をg因子とよぶ。このg因子を2とすると、トーマスの効果も考慮して、原子のエネルギー準位の微細構造、さらにまたパウリの原理を加えることによって周期律を含めて原子の諸特徴をみごとに説明できることがみいだされた。
[小川修三・植松恒夫]
スピン演算子
量子力学では、物理量は状態関数に対する演算子として表現される。電子のスピンをどのように表すかという問題もパウリによって解決された。まず電子の状態を記述するシュレーディンガーの波動関数ψ(x)を2成分(2行1列の行列)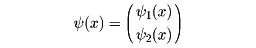
とすることによって、この波動関数に演算する次のような演算子S(=sx,sy,sz)、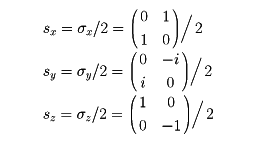
を導入することができる。この演算子は、電子が原子の周りを回転することによる軌道角運動量L(=Lx,Ly,Lz)と同じ代数的性質を備えており、角運動量としての資格をもっている。しかし普通の軌道角運動量の値がħを単位にして整数値であるのに対し、スピンは半整数の値をもつこと、またg因子が軌道運動による部分については1であるのに対し、スピンについては2であるなど、単純な自転描像ではかならずしも簡単に理解ができるとは限らない面がある。これらの問題は、ディラックの相対論的電子論の提唱をまって解明されることになった。
一般にスピンの値がħを単位にして整数値をとる粒子をボソン、半整数値をとる粒子をフェルミオンという。前者はボース‐アインシュタイン統計、後者はフェルミ‐ディラック統計に従う。光子、グルーオン、ウィークボソンなどの力を媒介するゲージ粒子はスピンが1でボソン、物質を構成するクォークやレプトンはスピンが1/2でフェルミオンである。フェルミオンは同じ状態には1個の粒子しか存在できないというパウリの原理に従う。力の統一にはフェルミオンとボソンの間を関連づける超対称性とよばれる対称性が重要な働きをすると考えられている。
[小川修三・植松恒夫]
核スピン
原子核の構成要素の一つである陽子は、電子と同じくスピン1/2をもちパウリの原理を満たす粒子(フェルミ‐ディラック粒子)であることが、水素分子の比熱の問題の解明のなかで明らかになった。もう一つの要素である中性子も、電荷が0という点を除いて陽子と同じ性質をもつ。陽子・中性子を構成要素とする原子核は、これら粒子のスピンや軌道運動の合成による核全体の角運動量をもつ。これを核スピンというが、同時に構成要素の磁気モーメントの和からなる核磁気モーメントができる。この核磁気モーメントは、それと軌道電子の磁気モーメントとの相互作用により、原子のエネルギー準位のずれ、すなわち準位の超微細構造を与える。この構造から核のスピンを決定できる。
一方、核子は三つのクォークからなるが、核子のスピンがその構成要素のクォークやグルーオンにいかに担われているかが、偏極ビームおよび偏極ターゲットを用いた核子の深非弾性散乱の実験で研究されている。これまでのところ、素朴なクォーク模型の予想とは異なっており、クォークやグルーオンの固有のスピン以外に軌道角運動量からの寄与も含めて、核子スピンの起源の問題として追究されている。
[小川修三・植松恒夫]
『朝永振一郎著『スピンはめぐる』(1982・中央公論社)』▽『亀淵迪・原康夫・小寺武康編、朝永振一郎著『角運動量とスピン』(1989・みすず書房)』▽『久保謙一・鹿取謙二著『スピンと偏極』(1994・培風館)』▽『宮下精二著『岩波講座 物理の世界 物質科学の展開7 量子スピン系――不確定性原理と秩序』(2006・岩波書店)』
百科事典マイペディア 「スピン」の意味・わかりやすい解説
スピン
→関連項目協同現象|クッシュ|グラビトン|K中間子|原子核|原子核物理学|原子構造|磁気共鳴|磁気モーメント|磁性体|ゼーマン効果|双極子|中性子|ディラック|ハウトスミット|バリオン|ヒッグス粒子|フェルミ粒子|ボース粒子
出典 株式会社平凡社百科事典マイペディアについて 情報
改訂新版 世界大百科事典 「スピン」の意味・わかりやすい解説
スピン
spin
静止している粒子の角運動量をスピンといい,粒子の自転の角運動量と解釈することができる。量子力学によれば角運動量の大きさは,ħ(プランク定数hを2πで割ったもの)を単位にして0,1/2,1,3/2,……という整数,あるいは半整数に限られる。ある素粒子,あるいはある状態の原子核はつねに一定の大きさのスピンをもつので,スピンはその粒子を特徴づける量子数の一つに数えられる。例えば電子,核子はスピンが1/2であり,α粒子やπ中間子はスピン0,重陽子などはスピン1である。スピンの大きさをS(×ħ)とするとき,スピンを空間のある方向へ射影した成分は,S,S-1,S-2,……,-Sという離散的な値のみをとりうる。したがってスピンSの粒子は2S+1個の状態(スピンの方向)をもつことになる。例えばスピンが1/2の電子は,主量子数,方位量子数など軌道で決まる状態のおのおのに対し,スピンが上向き,下向きの2種の状態がある。
電子のスピンは原子スペクトル中の二重項(接近したスペクトル線の対)の存在,異常ゼーマン効果などを説明する中で導入された。すなわち,アルカリ元素のスペクトルはボーアの原子論では理解できない二重項をもち,また磁場をかけたときのエネルギー準位の分離のしかたに異常性を示すが,1925年にウーレンベックGeorge Eugene Uhlenbeck(1900-1988)とハウトスミットSamuel Abraham Goudsmit(1902-78)は,電子が内部自由度をもち2個の状態をとりうるとすれば,これらの現象を説明できることを明らかにした。電子が二つの状態をもち磁場によって分離することは,銀の原子線が不均一磁場によって2本に分けられることで直接確かめられた。また元素の周期表を説明するためには,一つの軌道に2個まで電子が入りうることが必要で,これは電子のスピンが1/2(とりうる状態が2個)であることを示す。スピンは軌道角運動量と相互作用し(スピン軌道相互作用),両者が平行であるか反平行であるかによってエネルギーに差を生ずる。これによって原子のスペクトルに微細構造ができる。原子核がスピンをもつ場合は,電子のスピンとの結合によってさらに複雑な超微細構造をつくり,これから原子核のスピンの大きさを推定することもできる。一般に原子核のスピンは磁気モーメントの測定などから決めることができるが,短寿命のものや素粒子のスピンは,それらの崩壊,反応の角分布のようすなどから決められる。
粒子のスピンと統計とは密接な関係があり,スピンが整数のものはボース統計に従い,スピンが半奇数のものはフェルミ統計に従う。原子核の場合は,その構成子である核子がスピン1/2のフェルミ粒子であるので,その複合体の統計およびスピンが整数であるか半奇数であるかは,核子数が偶数であるか奇数であるかによって決まる。素粒子のスピンと統計の関係は,パウリによって相対論的場の理論から証明された。粒子はそれに固有の定まったスピンをもつのだが,一般により大きいスピンをもつ励起状態が存在する。素粒子のこのような励起状態の一群をレジェ系列という。ただし電子などのレプトンのレジェ系列の存在は明らかでない。
執筆者:宮沢 弘成
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「スピン」の意味・わかりやすい解説
スピン
spin
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
化学辞典 第2版 「スピン」の解説
スピン
スピン
spin
G.E. UhlenbeckおよびS. Goudsmitは,磁場中での原子スペクトルの分裂の仕方を説明するために,電子がその軌道運動の自由度のほかに自転の自由度としてスピン角運動をもつことを提唱したが,のちにP.A.M. Diracが相対論的電子論の立場から,スピンが電子のもつ内部自由度の一つであることを導き出した.量子力学的にはスピンsは角運動量演算子であり,s2 の固有値は,プランク定数hを2πで割ったℏを使うと,
s(s + 1)ℏ2
で与えられる.sはスピン量子数とよばれ,その値は1/2である.原子核を構成する陽子や中性子もスピンをもっており,それらのスピン量子数は電子と同じく1/2である.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
パラグライダー用語辞典 「スピン」の解説
スピン
出典 パラグライダー用語辞典について 情報
サーフィン用語集 「スピン」の解説
すぴん【スピン spin】
出典 (株)デジサーフ、(株)セキノレーシングスポーツサーフィン用語集について 情報
世界大百科事典(旧版)内のスピンの言及
【磁気モーメント】より
…この磁場は磁気モーメントがつくる磁場と同じで,もとの閉曲線に沿っての定常電流は磁気モーメントと同等の効果を与え,磁気モーメントとみなすことができる。電子は電荷をもち,自転運動(スピン)をし,また軌道運動をする。これらの運動が電子の磁気モーメントを形成し,この磁気モーメント,とくにスピンに基づくものが物質の磁気的性質を担っている。…
※「スピン」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
〘 名詞 〙 春の季節がもうすぐそこまで来ていること。《 季語・冬 》 〔俳諧・俳諧四季部類(1780)〕[初出の実例]「盆栽の橙黄なり春隣〈守水老〉」(出典:春夏秋冬‐冬(1903)〈河東碧梧桐・高...

