精選版 日本国語大辞典 「回転」の意味・読み・例文・類語
かい‐てんクヮイ‥【回転】
- 〘 名詞 〙
- ① くるっとまわること。また、まわすこと。
- [初出の実例]「銕石の心を回転して蜿媚の心を生じたと云心ぞ」(出典:四河入海(17C前)一四)
- 「壜を回転して燐をして普く壜内に布達せしめ密に口を栓塞し貯ふ」(出典:舎密開宗(1837‐47)内)
- [その他の文献]〔後漢書‐虞詡伝〕
- ② 平面や空間の図形や物体が、その各点の相互の位置関係を変えることなく、ある点や直線のまわりを一定角だけまわること、あるいは、まわりつづけること。また、そのまわす操作。回転移動。回転運動。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
- ③ 事に応じて次々と考えをめぐらすこと。
- [初出の実例]「寝てゐた間の頭の回転(クヮイテン)の工合によってどんな事にでもなって行く」(出典:金(1926)〈宮嶋資夫〉一三)
- ④ 物事が初めから終わりまでめぐる一巡。特に、飲食店などで、客が次々に入れかわる効率。また、投資された資金が回収されるまでの一巡。
- [初出の実例]「後から後からと、所謂『廻転』を急いで、追ひ立てられる感じと違って、『何卒ごゆっくり』と言はれてゐるやうで気持がいい」(出典:ロッパ食談(1955)〈古川緑波〉甘話休題III )
- ⑤ 「回転競技(かいてんきょうぎ)」の略。
日本大百科全書(ニッポニカ) 「回転」の意味・わかりやすい解説
回転(数学・物理学)
かいてん
数学用語と物理学用語の二義がある。
数学用語
平面の任意の点を定点Oの周りに定方向に定角度θだけ回すことを回転、または回転移動という(の(1))。この操作は、平面をそれ自身の上に写す写像と考えられる。O、θをそれぞれ回転の中心、回転角という。空間においては、定直線lを含む任意の平面をlを軸として定方向に定角度θだけ回転させるという操作は、空間をそれ自身の上に写す写像と考えられる。これを空間の回転移動といい、l、θをそれぞれ回転軸、回転角という(の(2))。とくに、180度の回転を、Oまたはlに関する対称移動という。空間の定点Oを通る直線を軸とする回転を全部ひっくるめてOの周りの回転という。平面と空間いずれにおいても、Oの周りの回転はすべて直交変換の一種であり、したがって合同変換の一種でもある。また、平面と空間いずれにおいても、Oの周りの回転が二つ与えられたとき、これらを続けて行った変換を最初の二つの回転の積と定義する。このとき、平面のOの周りの回転の全体がつくる群と、空間のOの周りの回転の全体が生成する群をともに回転群という。
平面や空間における回転という概念は次のようにして一般化できる。まず、nを自然数とし、実数の全体をRで表す。n個の実数の組(x1,…,xn)の全体をRnで表せば、Rnは普通の和とスカラー倍に関してR上のn次元ベクトル空間になる。A=(aij)をn次実正方行列とすると、Rnの元(x1,…,xn)を決めるたびにRnの元(y1,…,yn)が
yi=ai1x1+…+ainxn,i=1,…,n
によってただ一つ定まる。これはAをもとにしてRnからRnへの写像が定まったことを意味する。そこで、この写像をfAで表そう。明らかにfAは線形である。AがtAA=Iを満たすとき、Aを直交行列といい、fAを直交変換という。ただし、tAはAの転置行列を、Iは単位行列を表す。「直交変換はどんな図形もそれと同じ形の図形に写す」ことが知られている。Aを直交行列とすると、その行列式は±1であるが、とくに+1のとき、変換fAをRnの回転という(この意味の回転は中心とか軸という言葉を伴わないことに注意)。その全体は写像の合成を積として群をなすが、それをRnの回転群という。
平面に直交座標系を一つ定めると、平面はR2と同じになる。2次行列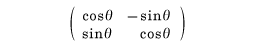
をAとおけば、Aは行列式1の直交行列で、直交変換fAは原点を中心とする角θの回転にほかならない。このとき、先に定義した平面の回転群とR2の回転群は一致することがわかる。同様に、空間に直交座標系を一つ定めると、空間はR3と同じになる。3次行列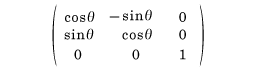
をBとおけば、Bは行列式1の直交行列で、直交変換fBはz軸を軸とする角θの回転にほかならない。このとき、先に定義した空間の回転群とR3の回転群は一致することが知られている。
[高木亮一]
物理学用語
回転運動をさす場合がある。
物理学でしばしば用いる演算子のことを回転またはローテーションrotationという。たとえば、流れのようすを表すには流れの各点に流速を示すベクトルを書けばよい。すなわち、各成分vx、vy、vzが点の座標の関数である速度ベクトル関数v(x,y,z)を与えればよい。これをベクトル場という。流体の渦の状態は、このベクトル関数からローテーションという微分演算子rotあるいはcurlを作用させて求めることができる。すなわち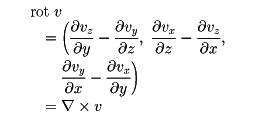
となる。磁場Hのローテーションは電場Eである。すなわちE=rotHとなる。
[田中 一]
最新 地学事典 「回転」の解説
かいてん
回転
rotation
回転変形による歪み。平面変形の状態を考え,変形前にきわめて近い位置にあった2点をP(x, y),Q(x+dx, y+dy)とし,変形によるP点の変位の成分を(u, v)とすると,
回転
地学的現象においては,内回転と外回転を区別。内回転は,物体内部に固定した座標系に関して,物体の変形によって起こる回転である。アフィン変形において,変形前の直線は変形後も直線であるが,その方向は変形によって一般に変化し,回転が起こる。ただし特別の場合にのみ,歪み主軸の回転が起こらない。この場合を非回転歪みといい,純粋すべりはその代表的な場合。圧延がほぼこれに相当。この場合にも主軸以外の方向では回転が起こっている。内回転に対し,物体内部に固定した座標軸が物体外の空間に固定した座標系に関して回転することを外回転という。例えば,両端固定した試料を軸方向から圧縮したときの歪み(キンクバンドなど)や,フレキシュラル・スリップ褶曲の場合の層面の褶曲で示される回転は外回転。後者の場合,地層内部において層面に固定した座標系に関する歪みによる回転が内回転。変形現象では外回転と内回転とが同時に起こり,外的制約のもとで互いに補い合っている。すなわち,同時に起こる外回転と内回転とのセンスは逆である。地学的現象においては,外回転のみならず内回転も不確定の場合が多い。その場合には,歪みの成分のうち純粋歪みしかわからない。
執筆者:植村 武・小島 丈児

出典 平凡社「最新 地学事典」最新 地学事典について 情報
改訂新版 世界大百科事典 「回転」の意味・わかりやすい解説
回転 (かいてん)
rotation
(1)平面上の各点Pに対し,Pをその平面上の一定点Oのまわりに一定角θだけまわした点をP′とするとき,PをP′にうつす対応を平面上の回転といい,Oを回転の中心,θを回転角という。空間の各点Pに対し,Pを一定直線lのまわりに一定角θだけまわした点をP′とするとき,PをP′にうつす対応を空間における回転といい,lを回転軸,θを回転角という。空間の1点Oに対し,Oを通る任意の直線を軸とする回転をOを中心とする回転という。平面の場合も,空間の場合も1点Oのまわりの回転の全体は合成を積として群をつくる。これを回転群という。この群は,平面の場合には可換群であるが,空間の場合にはそうではない。
(2)空間内に微分可能なベクルト場Vがあり,点(x,y,z)にベクトル(u,v,w)が対応しているとき,点(x,y,z)にベクトル を対応させることにより,新しいベクトル場が得られる。このベクトル場をベクトル場Vの回転といい,rotVまたはcurlVで表し,ローテーションVまたはカールVと呼んでいる。
を対応させることにより,新しいベクトル場が得られる。このベクトル場をベクトル場Vの回転といい,rotVまたはcurlVで表し,ローテーションVまたはカールVと呼んでいる。
→ベクトル解析
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「回転」の意味・わかりやすい解説
回転(ベクトル)【かいてん】
→関連項目渦度|演算子|ベクトル|ポテンシャル|マクスウェルの方程式
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「回転」の意味・わかりやすい解説
回転
かいてん
slalom
回転
かいてん
rotation
回転
かいてん
「ローテーション」のページをご覧ください。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
普及版 字通 「回転」の読み・字形・画数・意味
【回転】かいてん
字通「回」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
世界大百科事典(旧版)内の回転の言及
【回転運動】より
…太陽の周りの惑星の運動のように,大きさを考えず1点で表した物体(質点という)が他の1定点の周りで行う円運動や楕円運動をいうこともあるが,大きさのある物体の(変形を別途に考えることにして)運動を,並進運動と回転の合成として取り扱う場合の後者を指すのがふつうである。例えば,机の上を転がる円筒を考えると,その運動は軸の平行移動とその周りの回転とを合わせたものとみなすことができる。…
【回転運動】より
…太陽の周りの惑星の運動のように,大きさを考えず1点で表した物体(質点という)が他の1定点の周りで行う円運動や楕円運動をいうこともあるが,大きさのある物体の(変形を別途に考えることにして)運動を,並進運動と回転の合成として取り扱う場合の後者を指すのがふつうである。例えば,机の上を転がる円筒を考えると,その運動は軸の平行移動とその周りの回転とを合わせたものとみなすことができる。この場合,各瞬間の運動を,円筒と机の接触線を軸とした回転と考えることも可能である。…
【自転】より
…天体がその重心を通る軸のまわりに回転する現象である。複数の天体が共通重心のまわりを回る公転に対する語。回転の軸を自転軸,1回の回転に要する時間を自転周期という。一般に自転の状態は,自転軸の方向と自転周期によって定まる。地球の自転の場合,自転軸は天の北極を向き自転周期は1恒星日である。 天体の自転周期の測定には,天体の種類に応じていくつかの方法がある。太陽系の天体で表面に模様が見える場合は,その移動を観測して決める。…
【座標】より
…これに対し一般の平行座標系を斜交座標系skew coordinatesという。直交座標系では両座標軸の正の向きは,x軸を原点Oのまわりに時計の針のまわる向きと反対の向きに90度回転したときに,x軸の正の向きとy軸の正の向きが一致するように選ばれているのが通常である。このとき,両座標軸により分かたれる平面の四つの部分のおのおのを象限といい,図4のI,II,III,IVの部分を第1,第2,第3,第4象限という。…
【座標変換】より
…これを座標系の平行移動という。また,両座標系が同じ点Oを原点とする直交座標系で,I,JをOのまわりにθだけ回転した位置にI′,J′があるときは(図2),座標変換式は,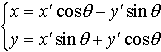 となる。これを座標系の回転という。…
となる。これを座標系の回転という。…
【ベクトル解析】より
…S上の点でのベクトル場Fのn成分をFnと書くことにし,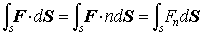 なる面積分を定義して,これをSを通過するベクトル流vector fluxという。
なる面積分を定義して,これをSを通過するベクトル流vector fluxという。
[勾配,発散,回転]
スカラー場φ(x,y,z)が与えられたとき,(∂φ/∂x,∂φ/∂y,∂φ/∂z)を成分とするベクトル場をφの勾配,あるいはグラディエントgradientと呼び,▽φ,またはgradφで表す。ベクトル場F=(Fx,Fy,Fz)に対して,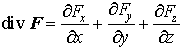 で定義されるスカラー場divFをFの発散といい,またx,y,z方向の単位ベクトルをそれぞれi,j,kとするとき,
で定義されるスカラー場divFをFの発散といい,またx,y,z方向の単位ベクトルをそれぞれi,j,kとするとき,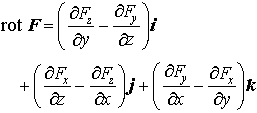 で定義されるベクトル場rotF(curlFとも書く)をFの回転という。…
で定義されるベクトル場rotF(curlFとも書く)をFの回転という。…
※「回転」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...