時間とともに,人間が自己および他者について認知し,語ろうとするときに登場する基本概念であって,通常はいっさいの事物の生起する舞台もしくは容器のごとき役割を果たしていると考えられる。時間をとめたとき,世界がそこにおいて存在するもの,といういい方もできよう。もちろん,このとらえ方自体,ある程度西欧的な哲学の伝統によりかかっており,例えば日本語における〈間(ま)〉は,明らかに時間と空間の双方を含んだ概念であるが,もともと〈時間〉とか〈空間〉という日本語がそうした西欧的背景のなかで用いられる習慣がある以上,ここでもさしあたって西欧的な概念史を問題にする。
西欧的空間概念の系譜
古代ギリシア文化圏で注目すべき空間論はデモクリトス,それにプラトン,アリストテレスに見いだせよう。デモクリトスにおいては,空間は,完全な〈空虚mēon〉(すなわちいっさいの存在の否定)としてとらえられ,それはまた,存在としての原子(アトム)が運動するための余地であるとみなされた。古代ギリシアでは,こうした存在の否定としての空間概念はきわめて珍しく,事実プラトンもアリストテレスもデモクリトスへの激しい反感を隠していない。プラトンの場合は,現実の経験的な事物を〈仮象〉と考え,それが〈真象〉たるイデアの模写であるという立場をとるが,空間はその意味では仮象でも真象でもなく第三の概念であるとされる。すなわち空間はイデアと同じように変化せず永遠にその同一性を保つが,しかしそれ自体としてなんら固有の形式を有しないという点でイデアとは異なるのである。経験的事物はイデアを父とし,空間を母として生まれる子であるともいわれる。一方アリストテレスは,物体どうしの相互の関係として空間をとらえる立場を打ち出した。しかし,具体的・現実的な空間としては,ギリシアでは,すでに述べたように,存在の否定である空虚もしくは真空を否定していたから,つねに何ものかがこれを満たしていると考えていた。いずれにせよこうしたギリシアの空間への強い関心が,空間関係を扱う学問としての幾何学の発達を促したと考えることができる。
他方宇宙全体の空間の構造についても,ギリシアでははっきりした概念があった。プラトンは,天体の世界と地上の世界とりわけ人体とを,マクロコスモス(大宇宙)とミクロコスモス(小宇宙)として対応させたが,アリストテレス以降は,天上界と地上界(月下界)とは,原理的,価値的に区別された。前者は完全な世界,後者は不完全な世界であり,それが各天体を支える球の重層的構造をとりながら(その中心に地上界がある),閉鎖的な球的宇宙を構成する,と考えられた。こうした球的空間秩序は,キリスト教的な世界観と結び付いて,一つのコスモス像を造り上げ,例えば中世都市のような現実の空間にも反映されることになった。実際ヨーロッパの中世都市空間は,自然条件の許す限り,円形で,求心,離心の方向性が明確に定まっており,この閉鎖的な都市空間は,近代に入って鉄道,自動車道路のごとき新しい要素が生まれても,容易に壊れないほど強固なものとなった。さらに,こうした空間構造としてのコスモス像は,舞台芸術のような空間芸術にも影を落としている。ローマのコロセウムをはじめ,中世,あるいはルネサンス期の劇場の構造は,決してそうしたコスモス像と無関係ではない。もっともコペルニクスの太陽中心説は,結果としてこうしたコスモス像の破壊を導いた。不完全な地上界が,完全な天上界を貫通して回転するということは,整然たる静的秩序のなかにあったコスモスへの挑戦になった。ブルーノ以降,宇宙の無限性や世界の複数性を論ずる可能性が開かれたのも,コペルニクス説がきっかけだったといえよう。
さて,近代初期に,ガリレイ,デカルト,ニュートンらの手で,運動の問題について,新しい理論体系が誕生するに伴って,その運動の生起する空間そのものに関しても,新しい展開が生じた。とりわけ空間解釈で重要なのはニュートンの〈絶対空間absolute space〉であろう。ただしニュートンの空間概念についてはやや誤解があって,絶対空間は完全に物理的な概念ではなく,むしろ,それ自体,神の〈感覚体sensorium〉のごときものだと理解されている(《光学》第2版)。それにしても,ニュートンにとって空間は,いかなる事物にも先立って存在し,いっさいの事物がそのなかで生起する〈容器〉のごとき概念として理解されていたことは確かであろう。デカルト的な三次元座標によって表現されるにしても,空間は三方向に一様に広がり,しかも,経験的事物とは無関係に存在するのである。その意味では,空間は,存在論的にいっさいの事物に先行するものであり,その点で〈絶対的〉でもあることになる。一方これに対して,アリストテレス的な関係論的解釈を洗練徹底し,ニュートンの絶対主義的な空間解釈と対立したのはライプニッツであった。ライプニッツは,事物の存在に存在論的に先立つ空間という考え方を否定し,事物の存在に伴って初めて現れるさまざまな関係(順序,位置など)がわれわれに空間という概念を与えるにすぎないと考えた。これを空間の関係主義的解釈と呼んでおこう。ニュートンの絶対主義とライプニッツの関係主義とは,その後も多くの追随者を生んで今日に至っているが,カントはいわば第三の道をとった。ニュートンが空間を存在論的にいっさいの事物に先行させ,ライプニッツが空間の存在論的身分を否定したのに対して,カントは空間を時間とともに,人間の認識の形式として,人間の側に求めた。認識が成立するとき,それはつねに時間と空間の形式の枠において,という条件があるのだ,とカントはいう。
このような議論が空間の存在論上,認識論上の身分を問題にしている間に,19世紀に入るや物理学の世界で,新しい展開が起こった。電磁気学における〈場〉の概念の成立がそれである。空間(少なくとも物理的な空間)は,それ自体ある物理的な性質を備えており,そのなかに存在する事物の振舞いに対して影響を与える,という理解がこの〈場〉の概念の中心にあった。言い換えれば,空間は単に事物を入れるいれもの,事物の生起する中立的な舞台ではなく,空間そのものがひずみをもち,機能をもつことになった。このような空間に対する新しい解釈は,その後心理学における〈生活空間〉,生物学における〈環境世界〉,あるいは文化人類学における〈文化空間〉など,他領域に及んでおり,人間の生きている空間が,時代,社会(共同体)によってさまざまなひずみをもっている,という基本的な認識は,現在広く共有されているといってよい。19世紀にもう一つ注目すべき事態が起こった。それは,空間関係を表現するための幾何学の多元性が認められたことである。空間関係は,ギリシア以来ユークリッドの幾何学によって一義的に記述されると考えられてきたが,19世紀に至って,非ユークリッド幾何学が出現して,空間関係の記述方法が幾通りもありうることが明らかになった。このことがのちに20世紀に入ってもう一つの空間概念の大きな変革を支えることになった。アインシュタインの手で生まれた相対性理論は,時間と空間との間のカテゴリカルな区別を取り除いたという意味で,やはり西欧的空間(時間)概念の歴史にとっては画期的なことだったといってよい。時間と空間は,独立の概念ではなくなり,相互に浸透し合った一つの連続体として理解されることになったからである。
ところで,すでに述べたように,西欧のコスモス像は都市構造などに反映される強固な秩序概念を形成していたが,19世紀からようやく崩壊の兆しが見られた。現代建築や都市設計の基礎を築いたミース・ファン・デル・ローエに典型的なように,それ自体秩序と意味をもった空間構造から,均質で等方的な格子構造への移行が見られる。近代的高層ビルは,空間を均質な格子に分割することを土台にして造られており,こうした流れは,元来コスモス像の希薄な日本では,とりわけ第2次大戦後の〈開発〉の結果として顕著である。例えば庄屋,鎮守の森,神社,川,墓場などがゆるやかなコスモスを造り上げていた日本の農村空間は,機能だけを目的にした高速道路や新幹線が縦横に走ることによって蹂躙(じゆうりん)され,大黒柱,床の間,水屋,土間などによって形づくられていた家屋内の空間構造も,戦後は団地などの集合住宅だけでなく,一般家屋でも無視されるようになった。こうした事態は,社会的な階級構造の崩壊と表裏をなすが,その意味では空間の〈民主化〉という比喩が成り立つかもしれない。しかし前にも触れたように,人間の生きる空間は,個人にとっても,社会共同体にとっても,つねに意味構造を備え,ひずみをもったものである。逆にいえば,人間が生きるということ自体が,そのまま空間をひずませている。そうしたなかで,空間があたかも均質,等方,平等,中立であるかのような虚構に立つことは,人間の生にとってかなり大きな無理を含むともいえる。交通機関や通信手段の発達によって,今日空間距離は確かに格段に克服されてきた。それだからこそ,現代のわれわれには,新しい空間構造の理念が必要とされているといえるのである。
→時間
執筆者:村上 陽一郎
文化人類学における空間
空間の距離的認識
人間の初原的な形での空間認識は物の存在を通して行われる。ある物の位置は,同じ空間にいる人間にとっては方向と距離によって決定される。方向の認識もさまざまの変異がみられるが,ここでは空間の距離的認識について述べる。
人間の無意識的な距離的認識については,ホールEdward T.Hallのプロクセミクスproxemicsが重要である。彼は,人間と人間が接触するとき,4種の距離のとり方があると主張した。密接距離(愛撫,格闘,慰め,保護の距離),個体距離(他者と恒常的に分離するための距離),社会距離(個人的でない,社会的な用件を処理する際にとられる距離),公衆距離(公的な場でとられる距離)の四つである。この4種の距離は状況によって使いわけられる。しかし,文化が異なると具体的な距離のとり方が異なり,誤解が生じる。たとえば,アラブ人にとっての個体距離はアメリカ人の密接距離に相当し,彼らが会話をしようとすると,アメリカ人はアラブ人はぶしつけで失礼な人間と思い,アラブ人はアメリカ人を距離をおく冷たい人間と思ってしまう。このように,四つの距離は各文化において認められるが,文化によってそのものさしが異なることを見いだした。
ホールの主張の中では,個体距離が特に重要である。人間は単に身体が占めている空間を占有しているのではなく,身体付近の一定の空間を個人の空間として占有している。このような空間は単に人間だけにとどまらず,非接触性の動物においても普遍的に認められる。それは進化のかなり早い段階で,同種内攻撃を回避させる方法のひとつとして出現し,なお人間にまで尾を引いているものと考えられた。個体距離は二つあるいはそれ以上の個体間においてみられる距離であるが,その基礎には,個体ごとに占有する空間というものがあるはずである,というのがホールの主張である。
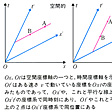
指示詞は,世界のどの言語にもみられる語群であり,かつ距離的な認識をその語の中に含んでいる。約500の言語の指示詞に関する空間的意味成分の分析から,人間は自己を中心とした,かなり普遍的な同心円状の距離的空間認識を潜在的にもっていることが明らかになった。それらは,〈手のとどく空間〉である触覚空間,〈声のとどく空間〉である聴覚空間,〈視覚のとどく空間〉である視覚空間と,もはやみることのできない視覚外空間である。これらの内,〈手のとどく空間〉である触覚空間は,個人が占有している空間,すなわち個体空間に一致するのではないかと考えられる。先に述べた文化による個体距離のとり方の違いは,個体空間の認識の違いにあるのではなく,個体空間のあつかい方の違いにある。すなわち,アラブ人にとって,ここちよく会話のできる状態は,個体空間がほとんど重なりあうほどの状態であり,アメリカ人にとっては,互いの個体空間をわずかに共有するほどの状態が安定した状態であるということになる。ただし,動物での個体空間を抽出することはむずかしく,人間の場合は言語をもちいてはじめて明らかになったにすぎない。
執筆者:吉田 集而
方位における空間認識
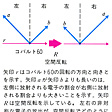
人は自分の住んでいる自然にもとづいて空間意識をもつ。地球が丸いということがわかり,地球が自転しつつ太陽の周囲を公転するという認識がもてた現在でも,太陽は東からのぼり,西に沈むという意識を人々はまだ用いている。日の本の国,日本という表現はやはり天動説的感覚で周囲をみている。1年を通じて太陽は出没の位置を変え,夏至と冬至の間の太陽の軌道差は地球各地の時の観念に差をもたらし,これは各文化の暦の差となっている。また空間意識の形成には山川草木やあらゆる森羅万象が作用しており,方位の認識には風が影響していることは柳田国男編の《風位考資料》がつとに明らかにしている。人は方位というと〈東西南北〉とか十二支を用いたものをもち出すが,実は地上各地の社会には独特の空間認識のしかたがある。日本においてこのような独自の民俗的空間認識を考証したものに移川子之蔵(うつしがわねのぞう)の《方位名称と民族移動並びに地形》(1940)がある。この中では,例えば台湾高山族諸社会の方位名称が,太陽,地形,風向,移住から生じていると実証されている。方位は一般に,単なる空間の分割ではなく,各空間に対する吉凶などの意味づけが伴っていて,これを方位観と呼んでいる。なお,動物における空間の問題については,〈棲分け〉〈縄張〉の項を参照されたい。
執筆者:倉田 勇


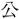 、北郭の民の
、北郭の民の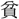 なるを憂へ、管子を召して問ふ。~管子對へて曰く、~千鍾の家は、
なるを憂へ、管子を召して問ふ。~管子對へて曰く、~千鍾の家は、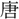 園(菜園)を爲(つく)ることを得ず、市を去ること三百
園(菜園)を爲(つく)ることを得ず、市を去ること三百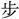 の
の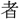 は、
は、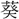
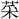 を樹うることを得ざらしむ。此(かく)の
を樹うることを得ざらしむ。此(かく)の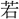 (ごと)くんば、則ち
(ごと)くんば、則ち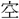
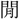 以て相ひ給
以て相ひ給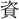 する
する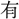 り。
り。