デジタル大辞泉 「環」の意味・読み・例文・類語
かん【環】[漢字項目]
1 ドーナツ形の玉。また、輪の形をしたもの。「環状/一環・金環・連環」
2 周囲を取り巻く。ぐるりと回る。「環海・環境・環視/循環」
[名のり]たま
[難読]
翻訳|ring
整数や多項式,あるいは二次の行列には,和および積がある。このように,数学で扱う対象には,次に述べる公理を満たす二つの算法〈加法〉〈乗法〉をもつものが多い。そこで,集合Aに,その2元a,bの和a+bを対応させる加法および積a・bを対応させる乗法が定義され,それらが次の公理を満たすとき,Aを環と呼んでいる。
(1)加法に関し,加群をなす。
(a) a+b=b+a
(b) (a+b)+c=a+(b+c)
(a,b,c A)
A)
(c) a+x=bは必ずただ一つ解をもつ。
(2)乗法に関し,半群をなす。
(d) (a・b)・c=a・(b・c)
……結合法則
(3)乗法が加法に対し,分配法則を満たす。
(e) a・(b+c)=a・b+a・c,
(a+b)・c=a・c+b・c
環Aの加法に関する単位元は,零元と呼ばれ,0で表す。Aの元aの加法に関する逆元を-aとかく。(c)(e)により,
(f) a・0=0・a=0,
a・(-b)=(-a)・b=-a・b
Aの元eで,任意の元aとの積が,
(g) a・e=e・a=a
であるものをAの単位元と呼ぶ。単位元は,存在すればただ一つで,ふつう1で表す。なお,数学の各分野で扱われる重要な環は,たいてい単位元をもつので,環といえば,単位元をもつ環を意味することが多い。また,
(h) a・b=b・a ……交換法則
も満たすとき,可換環と呼ぶ。
(1)数の環 整数の全体Z={……,-m,……,-2,-1,0,1,2,……,n,……}は,通常の加法,乗法に関し可換環をなし,有理整数環と呼ばれる。
(2)多項式環 可換環Aと,変数Xについて,Aの元を係数とする多項式全体は,可換環になる。Aの上の変数Xの多項式環といい,A[X]で表す。
(3)行列環 可換環Aの元aijを(i,j)成分とするn次正方行列全体は,行列の加法,乗法について,環をなす。A上n次行列環といい,Mn(A)で表す。n≧2のとき,例えば,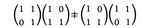 だから,非可換である。
だから,非可換である。
(4)その他 ある領域で定義された連続関数全体のなす環,ハミルトンの四元数,グラスマン代数などは,多元環と呼ばれ,多方面で重要な環である。
(1)零因子 環Aの,0でない元a,bの積a・bが,0であるとき,aを左零因子,bを右零因子という。二次正方行列環で,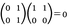 であるから,
であるから,
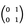 は左零因子,
は左零因子, は右零因子である。左,右零因子を総称し,零因子という。
は右零因子である。左,右零因子を総称し,零因子という。
(2)整域 零因子をもたない可換環を,整域という。有理整数環Zや,整域Aを係数とする多項式環A[X]は,整域である。
(3)逆元 単位元1をもつ環Aの元aに対し,a・b=b・a=1となる元bを,aの逆元といい,a⁻1で表す。逆元が存在する元を,可逆元,あるいは単元という。可換環A上のn次正方行列αが,可逆元であるための必要十分条件は,αの行列式がAの可逆元であることで,αの逆元をαの逆行列という。
(4)イデアル 環Aの部分集合Iで,左A-加群として,Aの部分加群であるものを,左イデアルという。同様に,右A-加群を考え,右イデアルを定義する。左イデアルかつ右イデアルであるものを,両側イデアル,またはイデアルという。
(5)部分環 環Aの部分集合A0が,Aと同じ算法に関し,環の構造をもつとき,A0をAの部分環という。例えば,有理整数環Zは,有理数体Qの部分環である。
(6)剰余環 環Aの両側イデアルIによる,Aの同値関係≡を,〈a≡a′⇔a-a′∈I(a,a′∈A)〉で定める。商集合A/≡の元,の和+,積・として,それぞれ同値類の元a,bをとり,それらの和a+b,積a・bが属す同値類を対応させると,A/≡に環の構造が与えられる。この環をAのIによる剰余環と呼び,A/Iとかく。有理整数環Zのイデアルとして,3の倍数全体3Z={……,-6,-3,0,3,6,……}をとると,Zの3Zによる剰余環Z/3Zは,3個の元,,からなる整域(さらに,可換体)である。
環Aから,環Bへの写像fが,
f(a+b)=f(a)+f(b)
f(a・b)=f(a)・f(b) (a,b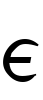 A)
A)
を満たすとき,fを準同型という。準同型の合成は,また準同型である。
さらにfが全単射であるならば,逆写像f⁻1:B→Aも準同型である。このとき,fを同型と呼ぶ。準同型f:A→Bの像Imf(=f(A))は,Bの部分環で,fの核Kerf(=f⁻1(0))は,Aの両側イデアルである。fは,A/f ⁻1(0)からf(A)への同型を導く(準同型定理)。逆に,環AのイデアルIに対し,Aから,AのIによる剰余環A/Iへの自然な全射πは準同型で,Kerπ=Iである。このように,Aの両側イデアルは,Aから,ある環への準同型の核として特徴づけられる。
上に述べた環の公理には,乗法の結合法則(d)が入っている。ところで,乗法の結合法則は満たさないが,他の公理は,すべて満たす重要な代数系として,リー代数などがある。このようなものも含め,環を定義することがある。その際には,乗法の結合法則を満たすものを結合環と呼ぶ。
執筆者:西村 純一
ドーナツ状をした玉で円孔の半径と辺の幅の等しいものをいう。天子が諸侯を封ずるときに賜る瑞玉(ずいぎよく)の一種。服飾や車輿(しやよ)の装飾にも用いられたが,耳環,指環,腕環などを指すこともある。環に似て辺の一部分の欠けているものを玦(けつ),平板で外辺の幅と円孔の直径とが等しいものを璧(へき)という。とくに,腰に帯びる環を玉環ともいう。《左伝》昭公十六年に〈宣子,環有り〉とあるのは,杜預の注によれば玉環のことであるという。
執筆者:杉本 正年
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
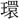

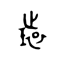


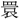 (かん)。
(かん)。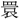 は死葬のとき、死者の復活を願って玉環をその胸もとにおき、復活の象として目をその上に加えた形。その玉を
は死葬のとき、死者の復活を願って玉環をその胸もとにおき、復活の象として目をその上に加えた形。その玉を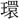 という。〔説文〕一上に「璧(へき)なり、
という。〔説文〕一上に「璧(へき)なり、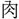 と好(孔)と一の
と好(孔)と一の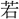 (ごと)き、之れを
(ごと)き、之れを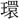 と謂ふ」とみえる。援引に用いる
と謂ふ」とみえる。援引に用いる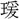 は「
は「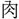 、孔に倍す」、つまり肉部の多い玉である。〔説文〕に
、孔に倍す」、つまり肉部の多い玉である。〔説文〕に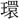 を
を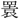 (けい)に従う字とするが、金文の
(けい)に従う字とするが、金文の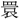 は目+衣+
は目+衣+ 、その
、その が環の形である。
が環の形である。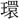 タマキ・トモキル・メグル・ユビマキ 〔字鏡集〕
タマキ・トモキル・メグル・ユビマキ 〔字鏡集〕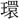 タマキ・ユビマキ・メグル・モトアシ・キル・トモ
タマキ・ユビマキ・メグル・モトアシ・キル・トモ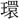 ・
・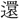 (還)hoanは同声。
(還)hoanは同声。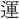 (運)hiu
(運)hiu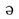 n、回hu
n、回hu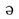 iと声義近く、みな旋回の意がある。
iと声義近く、みな旋回の意がある。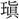 ▶・環
▶・環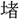 ▶・環佩▶・環
▶・環佩▶・環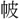 ▶・環璧▶・環抱▶・環擁▶・環流▶・環繚▶・環列▶
▶・環璧▶・環抱▶・環擁▶・環流▶・環繚▶・環列▶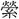 環・玉環・金環・銀環・
環・玉環・金環・銀環・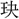 環・指環・耳環・珥環・珠環・周環・循環・繞環・旋環・刀環・佩環・珮環・半環・轡環・歩環・鳴環・游環・揺環・琳環・輪環・連環・彎環
環・指環・耳環・珥環・珠環・周環・循環・繞環・旋環・刀環・佩環・珮環・半環・轡環・歩環・鳴環・游環・揺環・琳環・輪環・連環・彎環出典 平凡社「普及版 字通」普及版 字通について 情報
任意の二つの整数の和と積はまた整数になる。この整数の和と積の性質を調べ、整数全体の集合Zの性質としてとらえると、環という概念に達する。すなわち一般に、集合Aに和と積とよばれる2種類の二項演算が考えられ、和についてはAが可換群になり、積については、結合律
(ab)c=a(bc) (a, b, c∈A)
を満たし、和と積の間には、分配律
(a+b)c=ac+bc,
a(b+c)=ab+ac
(a, b, c∈A)
が成り立つとき、Aを環という。とくに環Aが積に関して、可換律
ab=ba (a, b∈A)
を満たすとき、Aを可換環という。
整数全体の集合Z、多項式全体の集合C[X]はともに可換環である。また、n次正方行列全体の集合Mn(C)は環であるが、n≧2のときMn(C)は可換環ではない。このように環になっている集合はたくさんある。これらの共通した性質を研究するのが環論である。環Aには、Zの0のように
a+z=z+a=a (a∈A)
を満たす特殊な元zがある。このzを環Aの零元という。多項式環C[X]の零元は零多項式であり、行列環Mn(C)の零元はn次正方零行列である。
環Aの零元以外の元全体の集合が積に関して群になっているとき、環Aを体(たい)という。有理数全体、実数全体、複素数全体はそれぞれ体であるが、Zは体でない。環Aに、Zの1のように
ae=ea=a (a∈A)
を満たす特殊な元eがあるとき、このeを環Aの単位元という。
環は単位元をもつとは限らないが、もてば、ただ一つである。Zは単位元1をもつが、偶数全体の集合は単位元をもたない可換環である。また、C[X]、Mn(C)の単位元は、それぞれ、定数多項式1、n次単位行列
En=(δij)
(δijはi=jなら1、i≠jなら0)
である。
[菅野恒雄]
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
出典 株式会社平凡社百科事典マイペディアについて 情報
…石庖丁形のものは前11世紀ころに終末期に達し,骨製の鋤先をかたどったものは前5世紀の秦にわずかに残存する。この時期に特徴的な玉器としては,ほかに断面がT字形の環があり,この玉器は前2千年紀後期にもとづく。 前14世紀~前10世紀ころ,すなわち殷王朝後期から西周前期にかけての時期には,自然の動物や想像上の動物をかたどった小型の装身具,護符,愛玩品が多く作られた。…
…昆虫などでは主として彩色によって,魚や哺乳類あるいは昆虫の中でも甲虫類などでは体の一部に傷をつけて標識する。しかし最も一般に用いられるのは魚類におけるタグtagと鳥類における足輪(リング)ringである。以下鳥類の標識を中心にその概要を述べる。…
…装身具の一種。指輪はほかの装身具より文化性が高いといわれる。未開社会では首飾,腕輪,耳飾などを用いるが,指輪はあまり用いない。つねに狩猟や採集,あるいは農耕にたずさわっている人々には,指輪がじゃまになるからである。バビロニアやアッシリアでも指輪は用いられていなかった。指輪の歴史が始まるのは古代エジプトあたりからで,金のほか貝殻や軟らかい石や紫水晶のものがつくられ,大衆用には陶器のものがあった。エジプトでは指輪にスカラベを彫ったもの,あるいは指輪の飾台(そこに認印のしるしが彫られた)をスカラベ形にしたものが幸運のしるしとして用いられた。…
※「環」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
目次 飼養文化 北アメリカ 北方ユーラシア偶蹄目シカ科の哺乳類。北アメリカでは野生種はカリブーcaribouと呼ばれる。角が雄だけでなく雌にもふつうある。体長130~220cm,尾長7~20cm,...