目次 運動観の歩み 物理学における運動 運動の記述と座標系 座標系のえらび方 運動の法則 重力場での運動 束縛運動 質点と質点系 剛体の運動 相対運動 絶対運動の否定と相対論的運動方程式 量子力学での運動 生物における運動 植物の運動 動物の移動運動 遊泳swimming 匍匐creeping 歩行walking 跳躍jumping(leaping ) 走行running 飛翔flying 腕わたりbrachiation ヒトの運動 運動のメカニズム 運動の中枢性制御 運動時におけるエネルギー代謝 運動時における身体の諸変化 運動という概念を最も広くとるとき,それは,この世界におけるいっさいの〈変化〉を指すと考えられる。そしてこのような世界の〈変化〉一般を論ずるという意味でなら,中国,インドその他の古代文化圏にも,運動論はあった。むしろ,形而上学のみならず,魔術や呪術的世界観さえ,運動を論ずるものであったと見ることができる。
運動観の歩み 古代中国の形而上学体系として知られる《易経》は,もともと〈易〉の文字がトカゲ,あるいはヤモリをかたどった文字であるともされることからも明らかなように,(体色の)〈変化〉の象徴であり,結局は〈変化の学問〉を意味したし,それはのちに陰陽,五行,太極などの概念と結びついて,万物の起源たる唯一者〈太極〉からさまざまな物質や現象が生み出されて,世界となるための〈変化〉の原理を説明する,独特の運動論を構成したといってよい。ヘブライ思想とギリシア思想の混血から生まれたカバラ もまた,同様に根元をなす一なる基本原理から,多くの形而上学的しかけを用いて,自然界のあらゆる事物が生み出される過程,すなわち〈変化〉について統一的な説明を与えようとする知識体系といえる。ヘルメス思想 ,インドのアートマン理論など,こうした〈変化〉=〈運動〉にかかわる学は数多い。
しかし,今日われわれが運動という概念でとらえる概念形成に,最も直接的にかかわっているのは,古代ギリシアの形而上学体系であろう。もちろん,ギリシアにあっても,運動は,必ずしも,物理的な意味,つまり物体の位置運動としてのみとらえられたわけではない。アリストテレス は,一般に運動を,可能的なものから現実的なものへの〈変化〉として措定している。そこには,量的変化(増減,膨縮など),質的変化(物質の色の変化など),生成消滅(実体上の変化)が,位置運動のほかに,運動として数えあげられていた。位置運動に関しては,自然運動と強制運動が区別される。前者は,その運動体の本性に従って起こるものであり,完全さをその本性とする天体の世界にあっては,位置運動としてただ一つ許された等速円運動がそれであった。また,不完全さを宿命とする月下界にあっては,その世界を構成する土,水,空気,火がもつ本性(前3者は〈中心に向かう〉傾向,後1者は〈中心から離れる〉傾向)に従った垂直落下(もしくは垂直上昇)が自然運動である。強制運動は,他から直接運動力を与えられ,むりやりに動かされて生ずる運動であって,月下界の運動のほとんどすべてがこれに属する(天上界には強制運動はない)。こうして天体の位置運動は,多くの等速円運動を組み合わせて記述する,落下運動は宇宙の中心たる地球(の中心)に向かって起こる,などというギリシア的な宇宙論の基本了解が生まれる。
もとより,強制運動と自然運動の区別も,ギリシアの自然観のなかで,とくに生命体を照準したときには微妙にゆれ動く。生物がみずからの身体を動かす〈力〉は,そのもののもつ〈アニマ〉に由来するが,そうしたアニマを自然物のどこまで広げるかによっては,自然運動における〈本性〉の概念が影響されるからである。例えばアニミズム の傾向の強いプラトン主義あるいは新プラトン主義 では,天体の〈本性〉は,むしろそのアニマによる〈意志〉に接近し,ほとんど同義になる。こうして古代ギリシア・ローマ世界の運動観は,さまざまな考え方の可能性を重ね合わせた状態にあったということができよう。
近代科学の成立とともに,運動の問題は,もっぱら物理学とりわけ力学的側面に集約されていくが,それは,このようなギリシア的な運動観のなかから,強制運動,つまり運動力と運動の関係のみに視点を据えた論点に,するどく照明を当て,他の運動観をそれぞれ別個の場所へと分類した上で捨て去った結果であった。その意味で,運動に関する統一的視点は,近代の深まりとともに失われていく。さてギリシア的な強制運動の理論と,近代力学のそれとの根本的な差は,運動力が運動体に何を与えるか,という問題である。前者はそれを運動そのもの(つまり〈速さ〉)と考え,後者はそれを運動の変化(つまり〈加速度〉)と考えているからである。近代力学の成立はニュートン の運動法則の成立に重なるといってよいが,アリストテレスからニュートンまでの2000年の時間のなかで,古代世界,ビザンティン,イスラム,中世ヨーロッパを経て熟成した運動概念についてのさまざまな研究の歴史の延長上に,ニュートンの運動法則が存在する。しかし,運動の問題についてニュートン力学 があまりにもみごとに一つの解決を与えたがために,もはや今日,運動を広く変化一般として論ずることは不可能になった。したがって,ここでは,いくつかの側面から,運動を別個に扱うほかはないことになる。村上 陽一郎
物理学における運動 運動の記述と座標系 (1)直線運動 物体が一つの直線の上を運動する直線運動では,その上のある点Oから測った物体の位置座標x が時間t の関数x (t )としてどう変化するかがわかれば運動がわかったといってよい。運動について最も基礎的概念の一つは物体のもつ速度であろう。いまの場合,ある瞬間t における速度v というのは,時間t とt +⊿t (⊿t >0)の間の平均速度をv t を0に近づけたときの極限値だと考える(v =ẋ と書く)。一般に速さといえばv の絶対値を指すが,速度といえば符号も含めて考える。ある瞬間にv >0ならば物体はx の増す方向に運動しつつあり,v <0ならば逆向きに運動していることになる。止まっていた物体がしだいに速度を増し(つまり加速し),ある正の速度をもつ段階では,速度の増加率,いいかえると加速度a (v a は平均加速度をā とし,t を0に近づけたときの極限値である。簡単な直線運動の例としてa (t )=a 0 の等加速度運動を考えると,t =0での位置座標x 0 ,速度v 0 とすると,x (t )=x 0 +v 0 t +1/2(a 0 t 2 ),v (t )=v 0 +a 0 t となる。また,振幅A ,角振動数ωの単振動では,x (t )=A cosωt ,v (t )=-A ωsinωt ,a (t )=-A ω2 cosωt =-ω2 x (t )である。
(2)平面や空間内での曲線運動 一般の運動のときにはある定まった点(原点O)から物体の位置Pに向けて引いた矢印,すなわち位置ベクトルr O P の動きが時間t の関数として知れれば運動がわかったといえる。r t )を与えることは,平面または空間に固定した座標系に対するr x ,y )または(x ,y ,z )をt の関数として(x (t ),y (t ))または(x (t ),y (t ),z (t ))のように与えることと同じである。このとき,物体が平面または空間に描く曲線を軌道という。r r t )はt を補助変数とした軌道の方程式である。速度ベクトルv t )は,r
の⊿t ─→0としたときの極限(ṙ r r t )での速さに等しく,軌道に対する接線の方向をもち運動の向きを向いている。二つの位置ベクトルr t +⊿t )とr t )の差⊿r r t )の端点からr t +⊿t )の端点に向けて引いた矢印に対応する。v ṙ ẋ ,ẏ ,ż )であるようなベクトルだといってもよい。加速度ベクトルa(t )はv t )の時間的変化率v t )に等しい。xy 平面上の運動の例として半径がR ,角速度がωの等速円運動の場合,r R cosωt ,R sinωt ),v R ωsinωt ,R ωcosωt ),a R ω2 cosωt ,-R ω2 sinωt )=-ω2 r
座標系のえらび方 運動は相対的なものであるから,運動を記述するのに動いている座標系を採用することもできる。例えば動いている電車の乗客にとっては,車内の物体の運動は電車に固定した座標系を用いて記述するのが自然であろう。しかしこの座標系では見かけの力を考慮しなければならないため,力学の立場からは必ずしも便利ではない。力学の立場では運動の法則が最も簡単な形をとる座標系,すなわち慣性座標系 (慣性系)を用いるのが望ましい。ふつうわれわれが地上の物体の運動に対して用いる地上に固定した座標系はこの慣性系に十分近いことがわかっている。このことは地上での実験をもとに発達してきた力学にとっては幸いなことであったというべきであろう。しかしこの座標系も地球の回転を考慮しなければならないような運動または現象,例えば人工衛星の運動やフーコー振子 などについてはもはや慣性系とはいえない。現在慣性系と考えられているのは太陽系の重心に原点があり座標軸が恒星のつくる天球に対して決まった方向に向いているような座標系である。
運動の法則 慣性座標系では次のような運動の法則(ニュートンの運動の3法則)がなりたつ。(1)慣性の法則 慣性系では力の働いていない物体は,加速度のない運動(静止または等速直線運動)をする。(2)運動の法則 運動量の変化は,及ぼされる力に比例しその力の及ぼされる方向に起こる。具体的に運動方程式の形に書くと,P m ×速度ベクトルv F
ṗ F ṗ p dt ) (1)
P v
または加速度ベクトルa=v
ma=F
で表される。(3)作用反作用の法則 二つの物体が直接お互いに及ぼしあう力(作用と反作用)は,同一直線上にあって大きさが等しく逆向きである。なおニュートンはこの3法則のほかに,力が平行四辺形の合成則にしたがう,つまりベクトルであることをつけ加えている。
(3)式の形の第2法則に現れる左辺の加速度は,速度の変化率という運動学的概念だからわかりやすいが,このままでは質量の定義がなされていない。ニュートン自身は物体の質量をまさにその物体に含まれる物質の量と考えていたのだが,具体的には(3)式と第3法則を用いて質量を定義することができる。例えば一つのやり方として次のようなことを考えればよい。単位質量の物体1と質量m の物体2をばねでつなぎ,ばねを伸ばして滑らかな水平面上で運動させる。このとき物体1,2の加速度の大きさの比a 1 /a 2 がm に等しい。質量がわかれば運動の変化を起こさせる原因としての力が(1)または(3)式によって定義できる。質量
重力場での運動 例えば(3)式から,質量m の物体に働く重力の大きさは,物体によらず一定である落下の加速度g(=9.8m/s2 )を用いてm gと表せる。逆に重力の作用の下での物体の運動は,自由落下,放物運動のどちらについても(3)式の右辺のFを鉛直下向きに向いた大きさm gのベクトルとしてこの運動方程式(位置座標に関して2階の常微分方程式 )を解き,物体の位置r t )を時間t の関数として求めることによって理解することができる。落下運動の場合にはその鉛直方向の位置座標z (t )は,t =0における位置座標および鉛直方向の速度をそれぞれz 0 ,w 0 として,z (t )=z 0 +w 0 t -1/2gt 2 で,また放物運動はこれと水平方向の運動x (t )=u 0 t の組合せとなる(u 0 はt =0における水平方向の速度)。同じ力の下での運動形態,または軌道の違いは,初期条件(t =0での物体の位置と速度)の違いに対応する。ニュートン以前の考えには運動形態の多様性をそれぞれの場合の力の多様性のせいにする先入観があったが,ニュートンの理論によって同じ力の下でもいろいろな運動の形態がありうること,逆にいうと月の運動にしろ人工衛星の運動にしろ,また惑星,すい星のそれにしろすべて地球または太陽の万有引力の下での運動として統一的に理解されることになった。万有引力の法則はあらゆる2物体間に働き,2物体の質量をm 1 ,m 2 ,2物体の距離をr としたとき,F =μ(m 1 ・m 2 )/r 2 で表される(μは万有引力定数 )。地上の物体が受ける重力はその物体に地球の各部分が及ぼす万有引力の総和にほかならない(厳密には,さらに地球の自転による遠心力が加わる)。
束縛運動 上にあげた例は力(重力,万有引力など)がわかっていて運動(軌道)を調べることのできる例であったが,束縛運動のように軌道があらかじめ与えられていてそれからそれに対応する力が決まってくる場合もある。斜面(またはもっと一般に与えられた曲面)上の運動とか,長さl の糸の端につけたおもりの水平面内での等速円運動などがそれである。このようなときには斜面上に物体を保たせようとする抗力や糸の張力が運動から逆に定められることになる。例えば後の場合糸の張力T はmv 2 /l でなければならない。束縛運動
質点と質点系 ここまでのところで,漠然と物体と呼んですませてこられたのは,実は運動に際してその物体の大きさを気にする必要のない場合を考えていたからである。このような場合力学ではもう少し厳密に,質量をもつが点と考えてよい理想化された対象すなわち質点という概念を導入する。すなわちこれまでの話は質点の力学であった。これに対し大きさをもった物体は質点のあつまり(質点系)であるとして取り扱う。同様に質量が変わる物体の運動も当然質点系の運動として扱わねばならない。例えばロケットは燃料を噴射した反動で推進されるのだから,たとえロケットを質点として扱うにしてもはじめは質点系と考えて運動方程式を導く必要がある。その結果によると方程式は,ṁ をm の変化率,v ṁ v
剛体の運動 質点系として典型的なものは変形の無視できる,固い物体の理想化としての剛体である。固定軸のある剛体の回転運動は軸のまわりの角運動量L ,慣性モーメント I ,力のモーメントN を用いて,運動方程式,
L N (4)
L =I ω (5)
(L dL /dt ,ωは角速度) (5)
から定めることができる。この方程式は剛体を微小部分(または質点)に分け,そのおのおのについてたてた(1)および(2)式の形の運動方程式から導くことができる。固定点のあるときの剛体の運動は,剛体の位置を指定するのに三つの角度(例えばオイラー角 )が必要なため,その変化を与える(4)式の形の三つの連立方程式 (角運動量ベクトルL L やN はベクトルに変わる)を解いて定めねばならない。最も一般的な剛体の運動は重心の運動とそのまわりの回転運動との重ね合せとして記述できる。重心の運動は質量として剛体の全質量m をとりFとして剛体に働く力の総和が重心に作用しているとして(3)式を用いることによって調べることができる。重心のまわりの回転運動については上述のオイラーの運動方程式を用いればよい。変形する物体(弾性体や流体)の運動については,やはりその微小部分が時間的にどのように運動していくかを追求するための運動方程式を(1)~(3)式に基づいてたてることによって取り扱うことができる。このように古典力学の運動方程式はすべて(1)~(3)式から導かれるものといってさしつかえない。回転運動
相対運動 ニュートンの運動方程式(1)~(3)式は慣性系でなりたつと考えているので,これに対して加速運動をしている座標系で運動方程式を同様の形に表した場合,右辺に見かけの力すなわち慣性力が現れる。例えばある慣性系Kに対しξの加速度をもって運動している座標系K′での物体の加速度a a m (a′ F F m a F m ξとなるから,K′では加速度と逆向きの力-m ξが余分に働いていることになる。動き出した電車の乗客が進行方向とは逆に引き戻されるように感じる力はまさにこの慣性力である。この種類の力として日常経験されるものに,回転している系で働く遠心力 ,さらに回転系で運動しているときに働くコリオリの力 などがある。
絶対運動の否定と相対論的運動方程式 ニュートンの運動方程式はどの慣性系でも同じ形でなりたち(ガリレイの相対性原理),慣性系どうしの間はガリレイ変換 で結ばれている。すなわち(1)~(3)式はガリレイ変換に対して不変である。一方電磁気学の場の概念の確立に伴い,場の担い手つまり媒質としてエーテル の存在が当然のこととして信じられるようになった。このエーテルは,恒星に対して固定した座標系で静止しており,物体がその中を運動してもそれにひきずられることなく,光はその中をc =2.99×108 m/sの速度で伝わるとして多くの事実が説明できることがわかった。そこで19世紀末にいたって地球の公転運動を利用してそのエーテルに対する運動(絶対運動)が観測できるのではないかという考えが生まれ,そのような試みが行われるようになった。しかしこの考えもマイケルソン =モーリーの実験で,静止したエーテルに対する地球の運動がまったく検出できない(いいかえるとエーテルは地球とともに運動する)という否定的な結果が出るにおよんで重大な矛盾に出会うことになった。アインシュタイン はこれに対してすべての慣性系で光速がc である(いいかえるとすべての慣性系で,同じマクスウェル の方程式がなりたつ)という相対性原理を提出し,いっさいの困難をとり除いた。しかしこのことは同時に慣性系の間の変換としてガリレイ変換ではなくローレンツ変換 を用いなければならないことを意味したので,運動方程式もローレンツ変換に対して不変の形に修正しなければならなくなった。その結果は,(1)式はそのままで,(2)式のm を速度v によって変化する,m 0 はv =0の静止しているときの質量である。このような修正の結果が正しいことは光速に近い速度をもつ荷電粒子の運動で実際に確かめられている。相対性理論
量子力学での運動 これまで見てきたようにニュートン力学(古典力学)では,ある時刻に,例えば電子の位置と速度がわかればそれ以後の運動を完全に知ることができる。しかし量子力学の登場はこのようなマクロな世界で通用する概念が,原子の内部などのミクロな世界にはまったく適用できないことを明らかにした。量子力学によればそもそも電子がある時刻に,ある位置である決まった速度をもつような状態をつくりだすことは不可能なことなのである(位置と運動量の不確定関係)。それだけでなく,電子や陽子,中性子などでは粒子としての性質だけでなく,観測・実験のやり方によっては光同様,干渉,回折など波動としての性質を示す。量子力学的粒子の場合,われわれが知ることができるのは(一般に複素数の値をとる)波動関数Ψ (r t )だけであり,|Ψ (r t )|2 dV は時刻t に座標(x ,y ,z )の位置rの微小体積要素dV 中に粒子が存在する確率を与える。一般にΨ は空間内にある広がりをもっているので電子の位置の測定を繰り返すとその範囲で電子は違った場所に異なった頻度で見いだされることになる。Ψ (r t )の時間的変化はシュレーディンガー方程式 で定められる。その意味でこの方程式はニュートンの運動方程式に対応する基礎方程式であるということができる。実際これを用いて力F r U (r r r t )〉=∫dV r Ψ (r t )|2 が,運動方程式m 〈r¨ t )〉=〈F r r¨ d 2 r /dt 2 )。波動としての性質をもつのは名前のとおり波動関数Ψ (r, t )であるが,シュレーディンガー方程式をみたすこの関数はプランクの定数h を0に近づけていくと(m を無限に大きくしていったときも同様),それに対応して広がりが小さくなっていき,古典力学の軌道r=r t )上だけで値をもつ局在した関数に収縮していく。この意味で量子力学は古典力学を含んでいるとみなすことができる。しかしh は実際は0でないから量子力学的粒子は古典力学では考えられないふるまいを示す。その典型的な例は,古典粒子の通り抜けられない壁を越えて粒子(または波動関数)が滲み出してくるトンネル効果 であろう。そのほか古典力学の(有限領域での)定常運動では連続的にとることのできた力学的エネルギーの値が,とびとびの(離散的な)ものしか許されなくなるということなども顕著な事実として挙げることができよう。量子力学 田辺 行人
生物における運動 生物における運動もその力学的メカニズムについては無生物と変わるところがないが,それが生命活動の一つ,つまり外的な状況の変化に対する主体的・能動的な反応として現れるところに特質がある。したがって運動のエネルギー源 は基本的に自己のものでなければならない。運動に際して風や水流,重力といったものを補助的に利用することは多いが,それのみによってなされる他動的な移動は一般に運動とはみなさない。
運動能力は動物において高度な発達をとげているが植物にもいくつかの特徴的な運動様式がみられる。動植物を通じてその基礎となるのは細胞運動で,これには鞭毛運動,繊毛運動,原形質流動,筋細胞の収縮,細胞分裂時における細胞小器官の挙動などがあるが,多くの場合そのエネルギー源はATP である。多細胞生物ではこれらの個々の細胞運動の総体が器官・個体レベルでの運動となって現れる。また個体発生の過程においては形態形成運動と呼ばれる特異な運動が見られる。
植物の運動 動物細胞とは対照的に,植物細胞は一般に固い細胞壁で囲まれており,特殊な細胞(例えば,鞭毛を有する精虫)を除けばみずから運動する能力をもたない。一つの植物細胞の分裂によって生じた二つの細胞は隣合せに配置され,その後の発生段階においても相対的な位置関係は維持されるのがふつうである。したがって,植物の発生過程で見られる形態形成運動は細胞の分裂能や細胞伸長の方向性によって左右されている。外部からの刺激に呼応して起こる植物器官の屈曲運動(成長運動と膨圧運動に大別される。詳しくは〈屈性 〉〈傾性 〉の項目を参照)もまた細胞の分裂能や伸長性によっても説明することができる。一方,植物にあっても単細胞のバクテリアや藻類はかなりの運動性を有する。バクテリアの運動は鞭毛によるもので,光,化学物質,温度などに対して正または負の走性 を示す。刺激の種類によって走光性,走化性,走熱性などに分類され,バクテリアは主として刺激強度の時間的変化を認知して一方向的な運動を行う。藻類のクラミドモナス のある種のものでは,有性生殖を行う条件下においてアセチレン,エチレン,一酸化炭素,二酸化炭素への走化性運動を示す。また,珪藻で見られる細胞の滑走運動は有名であり,この場合,細胞からの粘液性物質(酸性多糖)の分泌が運動の原動力であると考えられている。変りものの生物として知られている変形菌類は,分類学的には植物と動物の両方に位置づけられており,生活史のなかで独特の挙動を示す。例えば,細胞性粘菌では動物的な相と植物的な相が生活史のなかで時間的に完全に分離しており,子実体形成の段階で最終的な分化をとげる細胞は細胞壁をもつ点において植物的である。しかし,子実体形成以前においてはすべての細胞はアメーバ状であって,仮足を形成しながら運動する。アメーバの集合時に見られる指向的な走化性運動および多細胞体の極性的な移動運動,これらはアメーバの仮足の一方向的な形成に基づいて起こる。この場合の細胞運動の基礎機構は,動物の非筋肉細胞のそれと大差ないと考えられるが,環状AMPをはじめとする走化性物質がいくつか同定されその初期反応が若干明らかにされていることを除けば,まだ不明な点が多い。細胞内での運動としてはブラウン運動以外に顕著な原形質流動が認められる。動物細胞にくらべてより規則的な流動パターンを示す植物細胞,とくに車軸藻類の節間細胞や変形菌類フィザルムPhysalum の変形体を用いて流動のメカニズムの解析が進んでおり,細胞運動におけると同様に流動にも収縮性タンパク質(アクチン・ミオシン系)が重要な役割を果たしていることを示す事実が蓄積されつつある。前田 靖男
動物の移動運動 ごく一部のものを除き,動物は食物やすみ場,異性を求めて積極的に動きまわる。また餌となる動物は動くことによって敵から逃れる。このような移動運動locomotionこそ動物を動物たらしめた基本的な特徴といってよい。移動運動の様式には遊泳,匍匐(ほふく),歩行,跳躍,走行,飛翔(ひしよう),帆翔,ジェット推進などいろいろあり,そのために使われる器官(運動器官)や機構もさまざまである。筋肉運動の場合は,関節をもつ骨格とそれに付着する伸筋・屈筋の組合せが一般的であり,骨格は無脊椎動物では外骨格,脊椎動物では内骨格になる。
遊泳swimming 遊泳は液体状の媒質の中を,底面から離れて移動する様式であり,まず歴史的に最も古く現れたものと考えてよい。単細胞動物は,鞭毛か繊毛あるいは波動膜の運動によって動く。多細胞動物でも,多くの無脊椎動物の幼生やワムシなどは,体に生えた繊毛を巧みに動かして水中を泳ぐ。しかし多くの多細胞動物は,筋肉の働きで体を波状に動かして泳ぐ。遊泳性の環形動物などはその典型である。魚も基本的にはこの形の遊泳をするが,脊椎骨の出現によって,体全体は波状に動かず,ほとんど尾部だけを左右に強く振って泳ぐものも少なくない。水の抵抗によって生ずる反作用の前向きの分力が推進力となる。尾以外のひれは多くの場合平衡を保つためにしか使われない。水生哺乳類は陸生の祖先の運動様式とそれに対応する体の構造のために,水平についた尾を上下に振るとともに,四肢の変形であるひれも使う。付属肢をもつ節足動物も遊泳の際に肢(あし)を使う。甲殻類の付属肢の多くは平たい遊泳肢となり,櫓でこぐときのようにそれらを動かして泳ぐ。ケンミジンコ のように第1触角を使って,跳ねるように泳ぐものもいる。水生昆虫では3対の肢のうち,ふつう後肢が遊泳用の肢に変形しているが,水面を泳ぐミズスマシでは前肢がその役を担っている。いずれもこの肢をオールのように使って泳ぐ。急激な水流を作って泳ぐものもいる。クラゲは傘を開閉し,甲殻類は尾を急速に曲げ,二枚貝は急に殻を閉じ,また頭足類やトンボの幼虫は水管あるいは肛門から水流を噴出することによって,速やかに反対方向へ泳ぐ。
匍匐creeping 次に現れた様式は匍匐である。水中・陸上を問わず,底面に体をつけて支えながら動くものである。速度は一般にのろい。アメーバはいわゆるアメーバ運動によって物の上をはう。肢をもたない無脊椎動物は,筋肉の収縮によって体の一部の収縮と別の部分の弛緩を繰り返し,体に一定間隔で支点となる変形を生じさせて,これを前後の方向へ移してゆくことによって移動する。巻貝類の腹足に見られる足波や,ヒモムシ,ミミズなどの蠕動(ぜんどう)運動がその典型的な例である。ヘビが地上をはうときも,原理は同じであって,いくつかの点が支点となり,その後の部分を前方へひっぱる。支点になった部位では,地面との摩擦を大きくするため,うろこが立てられている。
歩行walking 肢をもつようになった動物では,歩行すなわち肢で体重を支えながら,肢の先を支点にして体を駆動する様式が現れる。歩行の際,どの肢がどのような順序で動くかは,動物の種によって決まっている。この場合には肢は車輪のスポークと同じように腰を中心に回転運動をする。なお,木登りや崖登り行動は,体重を支えるための爪や四肢の巧みな運動が関与するけれども,基本的には匍匐か歩行の応用と考えてよい。
跳躍jumping(leaping) 甲殻類や唇脚類のように,肢の数が多いものでは,いつもどれかの肢が底面についているが,昆虫類や脊椎動物のように肢の数が少なくなると,とくに強力な肢を急激に屈伸して,全部の肢を底面から離して体を移動させる跳躍が可能になる。ノミが跳躍するとき,ノミはまず〈かがみこむ〉ようにして,強い後肢を折りまげる。すると,後肢の根もとにあるレジリンという物質の塊がひずみ,ひずみエネルギー が蓄えられる。そして同じく後肢の根もとにあるキャッチ機構がはずされた瞬間,ひずんだレジリンがもとに戻り,蓄えられていたエネルギーが放出されて,ノミの体は空中高く跳躍するのである。動物の体が大きく重くなると,体長と跳躍可能な高さとの比は減少する。それは体重が増すほど跳躍後着地するときの落下速度が大きくなり,それだけじょうぶな肢が必要となるが,肢のじょうぶさは肢の半径の2乗倍にしかならないのに,重さは3乗倍になるから,どうしても追いつけないためである。
走行running 走行は連続的な跳躍とみなすことができる。走行が可能なのは哺乳類と鳥類だけである。走行のときの肢の動きかたは,歩行の場合とは異なることが多い。哺乳類では食肉類やウサギなどに見られるように,前肢2本と後肢2本とをそれぞれそろえ,体を背腹にしなわせながら走ることが多い。この形は水生哺乳類の遊泳の方式にひきつがれている。
飛翔flying 飛翔とは翼ないしそれに類似した器官によって,地上から離れて空中を移動することである。鳥類と昆虫類において,異なる方式の飛翔が見られる。鳥ではふつう,翼の打下ろし打上げに伴って,偏心した羽軸をもつ初列風切羽の1本1本の羽毛がねじれ,渦巻状の気流がなん本も後方に向かって送りだされる結果,推力が生じ,これによって空気中を前進する翼の本体が不動翼のように働いて揚力を生じる。つまりプロペラ機と似た原理によって飛ぶのである。一方,昆虫やハチドリのようにごく小型の鳥は,翼の角度をたえず変えながら打ち,推力と揚力を同時に得る。ヘリコプター と同じ原理である。コウモリもこれに近い飛びかたをする。これらヘリコプター型の飛翔をする動物は,一般に飛びかたがうまく,急上昇,急降下をはじめ,細かな動きができる。ハエなどは天井にさかさにとまった位置から瞬間的に飛びたつことができ,また長時間静止飛翔(ホバリング)をつづけることも可能である。ムササビやヒヨケザル,トビトカゲ,トビガエルなどは,翼に似た皮膜をもっており,これで滑空glidingする。翼竜の仲間も滑空によって飛んでいたと考えられる。トビウオは水中で尾を強力に振り,その勢いで水面上に飛びだし,長い胸びれを左右に広げて滑空する。大型の鳥も翼を動かさずに滑空することがあるが,多くの場合,上昇気流を利用して舞い上がったり舞い下りたりする帆翔soaringをしている。
腕わたりbrachiation 霊長類のうちの類人猿は,ひじょうに変わった移動様式をもっている。前肢で木の枝にぶら下がり,体を前後に振りながら〈腕で歩いて〉いく〈腕わたり〉であり,これが人類の直立二足歩行の能力を準備したといわれている。日高 敏隆
ヒトの運動 ヒトの身体は多数の関節でつながった骨組み(骨格)からなり,一つまたは二つ以上の関節にまたがって骨格筋 (横紋筋)が骨につながっている。骨格筋の両端は結合組織の腱によって骨に結合しているが,この筋肉の収縮,弛緩によって関節を軸とした運動が生ずる。すなわち,腕,脚などの体肢の屈曲,伸展によって身体各部の相対的位置が変化し,種々の姿勢をとる。さらに身体全体の空間上の位置をかえて移動することもある。いいかえると,静止した姿勢からの連続した変化が運動であるともいえる。運動には多数の形があるが,基本的なものとして,歩行や跳躍など主として下肢の筋肉の働きによる運動と,つかむ,持つ,投げるなどの上肢の筋肉の働きによる運動がある。ヒトでは,とくに手指の運動が精妙で高度に発達している。特別な形の運動として,外眼筋の働きで視線をかえる眼球運動や,顔面の表情筋による表情の変化などがある。これらの運動を可能にしている骨格筋はすべて神経の支配を受けているが,大脳の意志に基づく随意運動と,無意識に自動的に生ずる反射運動に分けることもある。
運動のメカニズム (1)関節 身体各部位の位置の変化は,筋収縮により関節 を軸とした回転運動に基づく。回転の面や範囲は関節の形によって決まり,多軸性,2軸性,1軸性の関節に分けることができる。多軸性関節は,肩関節や股関節のように凸面の関節頭と凹面の関節窩が球面状をなしていて,きわめて自由な運動が可能である。一般に,関節の回転軸を中心として体肢が身体軀幹から遠ざかる外転,接近する内転や,ひじ,ひざ,手首などの関節を軸とした屈曲,伸展,さらに腕,脚などを内側や外側にねじる回内,回外などの運動がある。一般に,ある関節の屈曲,伸展はその関節の屈筋と伸筋の働きでなされるが,この両者を互いに他の拮抗筋という。この場合,屈曲,伸展にそれぞれおもに働く筋肉を主動筋といい,同じ方向の運動をする筋肉を共同筋という。
(2)筋肉の収縮 骨格筋は存在する部位や機能から種々の大きさ,形をしているが,数百~数千本の直径10~100μの筋繊維でできている。筋肉の収縮(筋収縮)は,その筋繊維を支配する運動神経繊維を通って神経の興奮(活動電位 またはインパルス)が神経末端まで達し,さらに筋繊維に伝えられることにより生ずる。神経末端と筋繊維の接合部は神経筋終板と呼ばれる特殊の構造をしていて,インパルスが到着すると,神経末端部に含まれているシナプス小胞 からアセチルコリン という伝達物質が放出される。アセチルコリンは,神経末端と筋繊維のせまい間隙(100~300Å)を拡散して筋繊維膜の受容体(レセプター)と結合し,その部分の膜の脱分極(イオン透過性の上昇)を起こし終板電位を発生する。この終板電位が一定の大きさになると活動電位を発生し,筋繊維全体に伝わる。この筋繊維表面膜の脱分極が横行小管(T小管)を経て内部に伝えられ,内部の筋原繊維を構成するアクチンフィラメント とミオシンフィラメント が反応して短縮(収縮)を起こす。
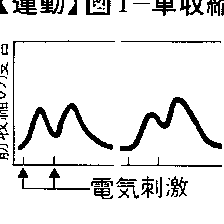
(3)筋収縮の様式 筋肉に直接またはその支配神経に1発の短い電気刺激を加えると,筋肉は数十ミリ秒の時間経過で1回収縮するが,これを単収縮という。この単収縮の過程は筋肉の種類によって異なり,速い収縮をする筋肉を〈速い筋肉fastmuscle〉,緩やかな収縮をする筋肉を〈遅い筋肉slow muscle〉という。速い筋肉は眼筋や下肢の腓腹筋などで,ミオグロビン含有量が少なく白筋ともいう。遅い筋肉はひらめ筋など姿勢の維持に働く筋肉で赤筋ともいう。この白筋と赤筋は,それぞれ相動性α運動ニューロン と持続性α運動ニューロンとによって支配されている。運動神経を通って短い間隔でつぎつぎにインパルスが神経筋終板に到着すると,単収縮がつぎつぎと融合し加重され,連続した強い収縮が引き起こされることになるが,これを強縮という(図1)。この型の収縮は単収縮の数倍以上の張力を発生し,通常の運動はすべてこの型の収縮によってなされる。また弱い収縮の場合は少数の筋繊維の収縮でよいが,強い収縮を必要とするときは収縮する筋繊維の数が増加する。筋収縮
(5)相反神経支配 一般に,ある関節で屈筋の収縮により屈曲するとき,その拮抗筋である伸筋は抑制され弛緩する。逆に伸筋が収縮するときは屈筋が抑制され弛緩する。そのため脊髄には相反神経支配の機構があり,このしくみによって円滑な屈曲または伸展が可能となる。
運動の中枢性制御 意志に基づいてなされる運動すなわち随意運動を起こす運動司令は,大脳皮質から下行して脳幹,脊髄にインパルスとして最終的にα運動ニューロンを興奮または抑制することによって運動を制御する。したがってα運動ニューロンを最終共通路ともいう。この場合,α運動ニューロンの活動は大脳基底核,小脳,脳幹などの働きで調節され,それによって精妙で複雑な運動が可能となっている。一見,随意運動として合目的で円滑な運動も,その背後に比較的単純な脊髄,脳幹レベルでの反射に基づいていることがしばしばある。
(1)反射 反射とは,刺激により意識とは無関係に運動が生ずることである。反射を形成するためには,刺激を感受する受容器と,それに接続してインパルスを送る求心繊維,さらに脊髄または脳幹に存在する反射中枢でシナプスを介して遠心繊維(運動神経)に接続する効果器(筋肉)が必要である。これらの反射に関与する全経路を反射弓という。脊髄に反射中枢をもつ脊髄反射には伸張反射,屈曲反射,交叉(こうさ)性伸展反射などがあり,また脳幹に反射中枢をもつ反射には姿勢反射,呼吸反射,咀嚼(そしやく)反射などがある。
(a)伸張反射 これは筋肉とくに伸筋が一過性にまたは持続的に引き伸ばされると反射的に収縮が生ずるもので,筋肉の長さを自動的に制御し,とくに背筋や下肢伸筋の抗重力筋群によく発達していて,直立姿勢の保持に役だつと考えられる。この反射に属するものとして,膝蓋腱反射 (しつがいけんはんしや)やアキレス腱反射などの腱反射がある。この場合,伸張反射を起こす刺激として,腱をたたき筋肉を伸張する方法が用いられる。この反射の受容器は筋繊維に並列して数十個程度存在する筋紡錘 である。この筋紡錘中には錘内筋繊維が数本あり,ここにIa求心繊維末端が付着している。筋肉が伸張されると筋紡錘もいっしょに引き伸ばされ,Ia求心繊維にインパルスが発生して脊髄に伝えられ,シナプス1個を介して直ちに前角のα運動ニューロンに接続して,伸張された筋肉が収縮する。この筋紡錘中の錘内筋繊維にはα運動ニューロンの近くにあるγ運動ニューロンから細い運動神経(γ運動繊維)が接続し,筋紡錘の伸張に対する感度を調節している(図3)。
(b)屈曲反射 皮膚に痛み刺激(侵害刺激)が加わると,刺激された側の体肢の屈筋が収縮し,伸筋は弛緩して肢全体を刺激から遠ざけるように屈曲する。例えば熱い物にふれたとき手を引っこめたり,足で画鋲を踏んだとき下肢を曲げたりする。この反射の求心路は皮膚や深部の痛み受容器を支配する細い求心繊維で,介在ニューロンを経由して多くの屈筋支配の運動ニューロンに興奮性に接続する。この反射は,刺激が強いと,同側の近くの関節の屈筋だけでなく,周辺の関節の屈筋にまで広がる。さらに対側肢の交叉性伸展反射を引き起こすこともある。
(c)姿勢反射 運動の際に頭や体が傾いたり首がねじれたりすると,自動的に体肢,体幹の筋緊張が変化し,適切な運動姿勢をとり平衡を保つ。この働きを姿勢反射といい,単一の反射ではなく,いくつかの要素的な反射の協調による。姿勢反射は脊髄,延髄,中脳と異なるレベルに反射中枢があり,上位レベルになるほど全身性に広範囲に生ずる。脊髄レベルの局所的な反射として交叉性伸展反射がある。これは屈曲反射で,一側の下肢が屈曲したとき,対側の下肢が伸展して体重を支え,身体の平衡を保つものである。全身の骨格筋に及ぶ反射として緊張性迷路反射と緊張性頸反射がある。緊張性頸反射では,首をねじると顔の向いた側の上下肢が伸展し,反対側の上下肢が屈曲する。例えば片手で伸び上がってボールをつかもうとしたとき,この姿勢をとる。また頭部を前屈すると上肢の屈曲と下肢の伸展が生じ,頭部の後屈ではこの逆の反射が生ずる。緊張性迷路反射では,頭部の空間的な位置,すなわち頸と体幹の関係は変えずに頭部を下げると,上肢が伸展し下肢が屈曲する。逆に頭部を挙上すると,上肢が屈曲し下肢が伸展する。これは,内耳の前庭器(卵形囊と球形囊)に働く重力によって受容器が興奮してインパルスを発生し,脳幹の前庭神経核を経由して脊髄のα運動ニューロンに影響を及ぼすことによる。この頸反射と迷路反射は実際の運動の際には協調して働き,両者の組合せによって種々の反射姿勢をとることができる。反射
(3)運動野 大脳皮質の中心前回(ブロードマンの分野4)にあり,この部位の電気刺激で反対側の体肢の運動が生ずる。運動野には,下肢,体幹,上肢,顔の順序で運動野の上方から下方に各部位の筋収縮を起こす運動部位が配列されている。また精密な運動をする手指やくちびる,舌などに対応する領域が広い。運動野には,個々の筋収縮を引き起こす直径約1mmの錐体細胞群が皮質表面に垂直に円柱を形成している。前運動野(分野6)およびその特殊な部位である補足運動野では,頭と眼球の協同運動,一定の姿勢運動など組になった運動が起こる。分野6の前方の分野8は眼球や瞳孔の運動を起こす領域である。また分野6の下方に隣接して発語に関与する運動性言語野(分野44)がある。小脳は前運動野と強く結びつき,運動のプログラムの作成に関与し,他方,運動の遂行に伴う末梢からのフィードバック入力を参照しながら運動のプログラムを修正すると考えられる。大脳基底核は,これらの運動を円滑に遂行させるのに必要な身体全体の姿勢と各筋肉の筋緊張を調節する。運動野 錐体路 は大脳皮質の運動野から途中でシナプス を介さずに脊髄前角の運動ニューロンに至る経路で,延髄の腹側の錐体を通り大部分の繊維は交叉して反対側の脊髄を下行する(図5)。しばしば皮質脊髄路ともいわれるが,錐体路の中には脳幹の脳神経核の運動ニューロンに至る経路も含める。錐体路には約100万本の神経繊維が含まれ,運動野以外に前運動野,頭頂葉の連合野などからの繊維を含んでいる。かつて錐体路は随意運動の司令を伝える経路と考えられたが,サルで錐体路を切断した後でも立ったり,物をつかんだりする随意運動は残るので,錐体路のみが随意運動の下行路というのは正しくない。しかし,錐体路の切断後はとくに手指の運動の速度と力の調節が悪くなり精密さを欠くようになるので,錐体路は随意運動のなかでも手指の運動に重要とみなされる。
錐体外路 は,錐体路以外,すなわち大脳皮質の運動領域から錐体路を経由しないで,脳幹の赤核,網様体,前庭神経核などを経て運動ニューロンに至る経路である。錐体外路は運動野,前運動野,頭頂連合野のほか,前頭葉の前頭前野や後頭葉,側頭葉からの下行繊維を含む。錐体外路は,錐体路が手などの熟練した随意運動を遂行できるように,姿勢および関連した筋活動を維持すると考えられる。大脳から脳幹の運動神経核を経て脊髄へ下行する経路には,おもなものとして赤核脊髄路,網様体脊髄路,前庭脊髄路がある。これらの経路は脊髄前角のαおよびγ運動ニューロンに興奮または抑制性の作用を及ぼす。前庭脊髄路は眼筋および頸筋の運動ニューロンの活動を調節するほか,体肢の伸筋支配の運動ニューロンには興奮作用,屈筋ニューロンには抑制作用を及ぼし,伸張反射弓を促進する働きがある。網様体脊髄路は,網様体の異なった二つの領域から相反する興奮および抑制の複雑な下行性作用を及ぼしている。赤核脊髄路の作用は錐体路と似ているが,上肢の屈筋活動を促進させるのに対し,下肢筋にはほとんど影響を及ぼさない。また小脳や大脳基底核などからの入力を受け,赤核を経由して脊髄の運動ニューロンに影響が及ぶ。
(5)小脳・基底核による運動制御 小脳と大脳基底核は協調して随意運動を制御する。小脳は運動時に身体各部の皮膚,筋肉,関節から体性感覚入力を受け,さらに前庭器,視覚器,聴覚器からも入力を受ける。他方,大脳皮質運動野から脳幹の橋核,下オリーブ核を経て運動司令の入力を受けている。小脳はそれらの入力を統合して,出力を脳幹の神経核および視床を経由して大脳皮質に送る。したがって小脳は随意運動に際し,運動司令を受け,同時に運動に伴うフィードバック情報を参照しながら運動の速度,範囲,力などの誤差の補正をするとみなされる。小脳半球の外側部はおもに体肢筋群の協調および手指の運動に関与し,傍虫部,虫部は体幹筋の筋緊張の維持,姿勢保持に関与する。大脳基底核は尾状核,被殻,淡蒼球からなる核群で,大脳皮質と密接に連絡し,大脳皮質によって開始された運動のための姿勢調節に重要な役割を果たす。尾状核と被殻を合わせて線条体という。また黒質,視床下核などの核を基底核に関連する核として扱うことがある。基底核は大脳皮質の運動野をはじめ,広範な部位から入力を受け,線条体-淡蒼球から視床を経て運動野にもどるフィードバック回路を形成する。また淡蒼球から中脳網様体,赤核を経て脊髄に至る経路もある。基底核は随意運動に際し,小脳と協同して体肢,体幹の筋緊張を持続的に調節する。とくに一定の姿勢を保持するため頸部,体幹,上下肢の空間的位置関係および運動の時間系列をプログラムする働きがあると考えられている。筋肉 →大脳皮質 青木 藩
運動時におけるエネルギー代謝 身体運動で主役を演ずる器官は骨格筋で,骨格筋は運動時そこに種々の化学変化を起こすが,運動が激しいほど消費されるエネルギーも増加するので,運動の強さをこの立場から量的に示すことができるわけで,一般にエネルギー代謝率というものが用いられる。基礎代謝 にあたるエネルギーである。安静時消費エネルギーというのは,いわば運動という仕事をする準備状態における代謝量で,基礎代謝量の1.2倍くらいとされている。運動時消費エネルギーというのが運動中の消費代謝量であって,これから安静時消費エネルギーを引けば,純粋に外的な仕事をするために消費された熱量になる。これが上式の運動代謝にあたるエネルギーである。エネルギー代謝率の例をいくつかあげると,安静休息0,座位0.3,歩行3,かけ足7,自転車乗り4,入浴1などである(なお夜間睡眠は基礎代謝の80~90%)。
エネルギー代謝量と疲労 との関係は,運動(または労働)の種類によって必ずしも一概にはいえない。エネルギー代謝率が4以上の運動の場合には,身体のほとんどすべての筋肉を用い,しかも動的な要素が多いので,この場合には疲労は主としてエネルギー消費量によって評価される。このように動的な激しい運動の場合には,疲労度はエネルギー消費量によって測られるが,一定の姿勢を保持するような静的仕事の場合にはこれと異なり,疲労の程度に比べてエネルギー消費量はきわめて少ない。例えば約50kgの重量を背負って立っているときのエネルギー代謝率は0.5という低い値を示す(ぶらぶら歩いているときでさえエネルギー代謝率は1.5~2である)。
運動時における身体の諸変化 運動時にはエネルギー代謝が盛んになるが,それに伴って酸素やエネルギー源を補給することが必要になる。そこで身体の諸器官にはこれに適応した変化が起こり,血液を十分に配布するために心臓の働きが盛んになり,血液のガス交換を十分に行うために呼吸活動が高まる。
(1)心臓と血管 心臓は運動の強度に応じて拍動数を増すと同時に,1回の拍動によって駆出する血液量も増加するので,毎分心臓から駆出する血液の量は平常の数倍にも達する。心臓に対するこのような効果は,血中の炭酸ガスや筋肉の代謝産物の増加によって延髄の心臓中枢が刺激され,心臓神経を介して心臓の働きを盛んにする結果起こるものである。運動開始と同時に心拍動数は増加するが,運動を開始しようと心構えをするだけでも拍動数が増すことが多い。これは大脳皮質が延髄の心臓中枢に対し神経性の影響を与えるためと考えられる。炭酸ガスその他の代謝産物は血管運動中枢を刺激して全身的に血管収縮効果を現し,心臓の活動増強と相まって全身の血圧を上昇させる。一方,これらの筋肉代謝産物は直接筋肉の毛細血管に作用してこれを拡張させ,筋肉組織中の流血量は増加する。
(2)呼吸 運動時には心拍動数の変化にほぼ比例して呼吸運動が速くかつ深くなる。これは,血中の炭酸ガスや乳酸の増加および酸素圧の低下により呼吸中枢(および頸動脈体,大動脈体)が刺激される結果である。呼吸も心臓の働きと同様に運動しようという心構えだけで変化するが,これも大脳皮質が延髄の呼吸中枢に対し神経性の影響を及ぼすためと考えられる。
(3)体温と発汗 運動に伴って筋肉に熱が発生するので,体温が上昇する。すると反射的に末梢の皮膚血管が拡張して皮膚からの放熱が盛んになり,また同時に皮膚汗腺が活動して発汗を生じ,蒸発熱によって熱放散が盛んになって体温の上昇が防がれる。山口 登


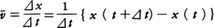 の⊿tを0に近づけたときの極限値だと考える(v=ẋと書く)。一般に速さといえばvの絶対値を指すが,速度といえば符号も含めて考える。ある瞬間にv>0ならば物体はxの増す方向に運動しつつあり,v<0ならば逆向きに運動していることになる。止まっていた物体がしだいに速度を増し(つまり加速し),ある正の速度をもつ段階では,速度の増加率,いいかえると加速度a(
の⊿tを0に近づけたときの極限値だと考える(v=ẋと書く)。一般に速さといえばvの絶対値を指すが,速度といえば符号も含めて考える。ある瞬間にv>0ならば物体はxの増す方向に運動しつつあり,v<0ならば逆向きに運動していることになる。止まっていた物体がしだいに速度を増し(つまり加速し),ある正の速度をもつ段階では,速度の増加率,いいかえると加速度a(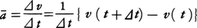 の⊿tを0に近づけたときの極限値である。簡単な直線運動の例としてa(t)=a0の等加速度運動を考えると,t=0での位置座標x0,速度v0とすると,x(t)=x0+v0t+1/2(a0t2),v(t)=v0+a0tとなる。また,振幅A,角振動数ωの単振動では,x(t)=Acosωt,v(t)=-Aωsinωt,a(t)=-Aω2cosωt=-ω2x(t)である。
の⊿tを0に近づけたときの極限値である。簡単な直線運動の例としてa(t)=a0の等加速度運動を考えると,t=0での位置座標x0,速度v0とすると,x(t)=x0+v0t+1/2(a0t2),v(t)=v0+a0tとなる。また,振幅A,角振動数ωの単振動では,x(t)=Acosωt,v(t)=-Aωsinωt,a(t)=-Aω2cosωt=-ω2x(t)である。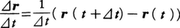
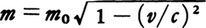 の形に変えればよいということであった。このm0はv=0の静止しているときの質量である。このような修正の結果が正しいことは光速に近い速度をもつ荷電粒子の運動で実際に確かめられている。
の形に変えればよいということであった。このm0はv=0の静止しているときの質量である。このような修正の結果が正しいことは光速に近い速度をもつ荷電粒子の運動で実際に確かめられている。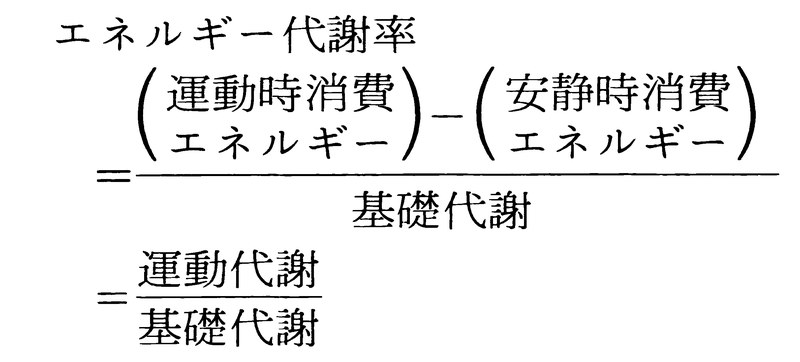




 動す。
動す。