目次 デカルト =ニュートン 的発想とその限界 場の概念の登場と展開 物理学における場 遠隔作用 と近接作用 場の概念の確立 量子力学 と場 重力場の理論 一般には，空間そのものが何らかの作用（物理的，心理的）をもち，そこに現象を生じさせると考えられるとき，その空間を〈場〉と呼ぶ。場の概念は，必ずしも〈場〉と呼ばれない場合も含めて，今日，科学の諸領域で重要な役割を果たしつつある。それは，一つにはニュートン力学的な遠隔作用 を前提とする力の概念に対抗して，またもう一つには原子論的発想に対抗して，とりあえずは19世紀に生まれた。したがって，出発点は物理学にあるといってよい。
デカルト=ニュートン的発想とその限界 ニュートン力学と呼ばれるものの本態は，実はデカルトの基本プログラムである。デカルトは世界を材料としての〈もの〉と，その材料のふるまい （運動）を定める運動法則とに還元するプログラムを立てた。デカルトにあってその両者は，創造主たる神によって原初的なものとしてつくられ与えられたが，それゆえに〈もの〉と〈運動〉とは，世の終りまで半永久的に保存されると考えられた。そこで世界は，〈もの〉と，それに外から与えられる〈運動〉とによって記述されることになった。皮肉なことにデカルトは真空 を認めなかったために原子論者にはなれなかったが，原子論における原子をデカルトの材料としての〈もの〉の具体像となし，一方，〈運動〉の法則にはニュートンの運動法則を採用することによって，このプログラムは理念上は完成したかに見えた。ある時点において作用している力や力学的状態を完全に把握・解析する能力をもち，宇宙の全運動を確定的に知ることのできる超人間的知性で，ラプラスによって想定されたことから，のちに〈ラプラスの魔〉と呼ばれたものはそうした状況の象徴ともいえる。
しかし，ここに解決されないで残された問題がいくつかある。第1に，ニュートンの運動法則における〈力〉は，いったいどのような機序で〈もの〉に働くと考えるべきか。例えば重力がその好例である。二つの〈もの〉の間に〈遠隔的〉に働く重力は，どのような作用機序によるのか。第2に，18世紀末からしだいに人々の関心をひき始めた電気や磁気において，その作用機序は重力のような〈遠隔作用〉として理解するだけでよいのだろうか。つまり，物体に対する力の遠隔的作用という形でそれ以上の説明を拒否する（それが《プリンキピア 》におけるニュートンの〈我は仮説をつくらず〉という言明の真意であった）ことに満足できないような状況が，19世紀に入ると生まれてきたのである。
場の概念の登場と展開 1820年H.C.エルステッドが電流の磁石に対する影響を明証する事実を発見した。電流を流した電線の傍らに磁石を置くと，電流の方向に対して直角に（もしくは円環をなすように）磁石が動く，という事実である。この事実は，それが電流であること（つまり静電気では起こらない），また従来の引力（静電気や磁力の場合には斥力も加わるが）のように，点と点との間に，直線的に働くのではないことなど，遠隔作用力で説明するには困難な性格をもっていた。そこからファラデー の磁場（電場）という着想が現れる。この着想の物理学的意味は重要であり，その説明とその後の展開については次項に譲るとして，より広範囲な文脈での意味もまた見逃し得ない。つまり，物質が存在する空間は，完全に中性的で等方・等質な性格をもつものではない，という認識をそれが生み出したからである。物体は等方・等質・中性の空間内にあって，ただ物体どうしの相互作用のみに注目すればよい，という原子論的な発想と，物質（もの）とそれに与えられる運動の2本立てで原理的にはすべての現象は記述される，というデカルトに淵源するプログラムとは，ともに修正を迫られることになった。
物体が存在したり，運動したりすること自体，空間を歪ませ，等方・等質・中性の空間を変形しているという認識からは，当然，物体もしくは物質ではなく，それまで単に物質にとってのいれものにすぎないとされてきた空間そのものに対する関心が引き出される。この新しい関心はひとり物理学にとどまらず，生物学，心理学，哲学などにも広がった。20世紀初頭，胚の発生，器官形成などの場面で，さまざまな異なった条件下にも等結果性equifinalityを実現するような〈場〉が生物体として考えられるというグルビッチA.G.GurvichやワイスP.A.Weiss以来の生物学上への〈場〉の応用が見られ，こうした考え方はベルタランフィ など現代のシステム論の原型をなすものとなった。さらにユクスキュル の〈環境世界Umwelt〉のように，生物にとっての環境空間は，決して客観的に等方・等質的なものではない，という考え方にも場の概念は取り込まれている。この路線上には，現代の動物行動学におけるプロクセミクス ，生活圏，なわばり ，すみわけ など，個体，群れ，種などさまざまなレベルでの生物の存在と環境空間とのかかわりに着目する概念系が見据えられる。
また心理学ではK.レウィンの〈生活空間〉が重要である。もともと心理的行動B を個人P と環境E の関数（B ＝f （P ，E ））としてとらえるという物理学的アナロジー を心理学に導入したレウィンは，環境すなわち心理的な作用をもった〈生活空間〉を心理現象の根本に据えようとした。現代では，このような考え方は社会や国家にも拡張され，グループ・ダイナミクス ，ゲーム理論 などに暗々裏にあるいははっきりした形で取り入れられている。さらにこうした発想は文化人類学 においても顕著である。E.T.ホールの個人のもつ個体空間〈バブルbubble〉のような着想から，一つの文化圏それ自体が一つの場として，人間行動を支配する“歪んだ”空間であると考えるエスノメソドロジー に至るまで，場の概念は広範に広がっている。
哲学においては，サルトルの〈状況〉や，実存主義における〈世界〉は，自己実現を可能にするものであると同時に，自己実現を限定する役割も担うと考えられる。こうした概念も特異な場所，意味空間としてのトポス というような考え方と並んで，諸科学における〈場〉の哲学的な定式化の試みと見ることができよう。もっとも，諸科学においては物理学からのアナロジーとしての場は発見誘導的な意味で，重要な役割を果たしたが，物理学における場自体の厳密な数学的定式化とは違って，精密化されるに従ってその領域特有の概念に転化される傾向があることは指摘しておくべきかもしれない。村上 陽一郎
物理学における場 空間的に分布する量で，とくに力や作用の伝達に関与するものを場，あるいは力の場と呼ぶ。古典物理学 でもっともよく知られているのは，電場や磁場であり，またこれらが物理学における場の概念の出発点である。特殊相対性理論 および一般相対性理論 において場という考え方はさらに本質的なものとなり，一方，量子力学では，粒子と場の二重性が明らかにされた。現在の素粒子論は，量子力学と特殊相対性理論とを結合させた場の量子論によって記述される。以下，まず静電場の説明から始めよう。
遠隔作用と近接作用 原点Oにある点状の電荷Q が，距離r だけ離れた点P（x ，y ，z ）に作る電場E kQ /r 2 （k は比例定数）で，Q ＞0ならばOからPを向き，Q ＜0ならばPからOを向くベクトルである。点Pに，もう一つの電荷Q ′をおくと，F Q ′E E Q とQ ′の間に働くクーロンの力を与えることがわかる。すなわち，電荷を結ぶ方向の，kQQ ′/r 2 の力である。もちろん，QQ ′＞0ならば斥力，QQ ′＜0ならば引力である。
しかしクーロンの法則では，離れた2点の間に直接力が働くと考えるのに対し，上述の考え方では，力は電場を介して伝えられると解釈する。すなわち，電荷Q は，まわりの空間に電場E Q ′は，その場所における電場から力を受けとるのである。第1の離れた2点間に直接力が働くとする考え方を遠隔作用と呼び，場を経由する第2の考え方を近接作用と称する。
ただ静電気力に限っていえば，二つの考え方は，同じ結果を得るための記述法の差にすぎない。しかし磁気に関する法則は，もっぱら近接作用論的に表現される。2本の平行直線電流I 1 ，I 2 の間に働く力を考えてみよう。まず電流I 1 はアンペール の法則によって，そのまわりに同心円状の磁場H I 2 があると，電流には，電流と磁場の双方に垂直な方向に力が働く。こうして，結局2本の電流の間に力が働く。この結果を，磁場を介さず，電流間の直接の力として導くことも不可能ではないが，きわめて複雑である。さらにM.ファラデーによる電磁誘導の法則では磁束の考え方が本質的であり，場の概念なしにこれを理解することは事実上できない。
場の概念の確立 電気，磁気の諸法則をまとめたマクスウェル の方程式は，完全に場の理論の形をとっている。しかし物理的な実体としての場の概念の確立にとって決定的であったのは，マクスウェルによる電磁波の理論である。マクスウェル方程式の解の一つとして，彼は真空中をc ≒3×108 m/sで伝わる波，電磁波が存在することを見いだし，これが光の本性であることを示した。電荷が振動するとそのまわりに振動する電場や磁場が生じ，それが離れた場所にある別の電荷に達すると，それを振動させる。すなわち，電荷から電荷へ，作用が電磁波を通じて伝達されるのである。ここまでは，静電気力の場合と同じであるが，注意すべきことは，作用の伝わり方に時間がかかることである。なぜなら光速c は有限の値をもっているからである。
これは，離れた電荷の間の空間に何物かが存在することを示唆する。ちょうど水面に石を落とすと，波が水面を伝わり，離れた点に浮かぶ落葉を動かすのに似ている。これこそ近接作用の考え方にほかならない。これに反し，遠隔作用論 では，途中には何もないと考える。したがって，作用が伝わるとすれば，それは瞬間的に伝わらなければならない。アインシュタイン の特殊相対性理論のもとでは，空間的に離れた2点における同時性は絶対的な意味をもたず，座標系の選び方によって変わるものであることが明らかにされた。遠隔作用論に特有の瞬間的な作用の伝達という考えは，この同時性の概念に基づいているので，相対論とは相入れない。こうして，相対論においては近接作用論的な場による記述が不可欠となる。
量子力学と場 特殊相対性理論以後，物理学における流れの一つは，微視的物理学の追究から量子力学へとつながる。ここでは，電磁場も光子という粒子像をももつこと，また逆に古典的には粒子と考えられる電子なども波動の性質を示すことが発見される。すなわち，ド・ブロイ ，E.シュレーディンガー の物質波の考え方である。このようにして場の概念は飛躍的に拡張され，粒子像との相補性という新しい面も出現したのである。
量子力学の完成後，多くの素粒子が発見されることになるのであるが，これらを記述する方法は，現在ではすべて場の形式を用いて行われる。これは前に述べたように，特殊相対性理論の要求に一致するようにするためである。作用の伝達は，1点における場の重なりおよび真空中の波動の伝播（でんぱ）の組合せによって表される。前者は場の相互作用と呼ばれる。量子力学によれば，これは，その場所におけるそれぞれの量子，すなわちその場に相当する粒子の生成，消滅を表す。このような事柄を整合的に記述する理論形式が相対論的な場の量子論であり，現在の素粒子論の基礎となっている。
ディラック の陽電子論は，このような理論形式の最初の物理的成果といってよい。これは，電子の物質波に相当する，フェルミオン場に関する理論であるが，電磁場と同じ範疇（はんちゆう ）に属するボソン場に関する最初の成果は，湯川秀樹による中間子論であった。中間子は，粒子像でみれば質量をもつ粒子であり，その反映として，対応する中間子場は有限の到達距離をもつ。これに対して電磁場は，無限の到達距離をもつといわれているが，これは静電場が～1/r 2 のようにふるまうことに対応している。一方，中間子場は～e ⁻μ / λ /r 2 のように，r ＞λに対して急速に小さくなってしまう。ここで到達距離λは，中間子の質量μとλ＝ħ/μc という関係にある（ħは，プランク定数h を2πで割ったもの）。
重力場の理論 特殊相対性理論以後のもう一つの発展は，アインシュタイン自身による一般相対性理論およびそれに基づく重力の理論である。ニュートンの重力は，静電気力と同じく遠隔作用的な力と考えられていたが，一般相対性理論では，完全に近接作用論的な場の理論として定式化される。この理論における重力の場，すなわち重力場は，曲がった時空の計量テンソルである。そして，マクスウェルの電磁波に対応して，真空中を光速c で伝播する波動の存在が導かれる。これが重力波である。重力の作用もこの重力場を通じて有限の時間をかけて伝達されるのである。この重力波を実験的に検知するための努力が現在精力的に進められている。
こうして電磁場と重力場は多くの共通点をもつ場の理論として定式化されることとなり，これらをさらに高い立場から統一的にとらえようとする統一場の理論が種々試みられた。なかでも，H.ワイルの理論が有名であるが，ここで提出されたゲージ理論 およびゲージ場の概念は，その後素粒子の基本理論として受け継がれている。相対性理論 →場の量子論 藤井 保憲
［名］
［接尾］助数詞。演劇で、一幕のうちで一区切りのつく場面を数えるのに用いる。「二幕三
〈ジョウ〉
〈ば〉「場合・場所・場面／足場・市場・急場・職場・相場・立場・墓場・本場」
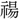(しよう)・湯(とう)の声がある。昜は台上に玉（日の形）をおき、その玉光が放射する形。玉による魂振りの儀礼を意味し、その儀礼を行うところを場という。〔説文〕十三下に「
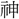を祭る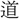
なり」とあり、両祭壇の間を場という。〔漢書、郊祀志上〕に「犧牲壇場」と称しているもので、墓祭のときには「羨道(えんどう)」（墓室に通ずる道）で行った。〔孟子、
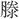文公上〕に、孔子の喪送の後、ひとり子貢が「室を場に
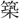き」三年の喪に服したことを記している。〔周礼、地官、場人、注〕に「地を
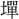(せん)を爲(つく)り、季秋に圃中を除して之れを爲る」とは、田中に「祭の場(にわ)」を作ることをいう。わが国の古訓に「には」とよみ、「斎場」をいう。なお〔説文〕には「一に曰く、田
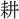さざるなり。一に曰く、
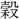を治むる田なり」とあり、「
立〕場 サカヒ・ミチ・バ・ミギリ・ニハ