デジタル大辞泉 「円」の意味・読み・例文・類語
えん〔ヱン〕【円】
2 平面上で一点から等しい距離を保ちながら動く点の軌跡(円周)と、その内部。「同心
3 《yen》日本の通貨単位。1円は100銭。明治4年(1871)の新貨条例により、両に代わって円が定められた。記号は¥。
[類語]円形・同心円・真ん丸・半円・楕円・長円・丸っこい・丸まっちい・丸丸・丸い・
( ③について ) 近世、小判の形から、「両」と同意に使われたが、明治四年(一八七一)「新貨条例」によって採用され、純金四分(一・五グラム)に相当し、それまでの一両、または永一貫文にあたるとされた。しかし、実質的に金本位制が確立して金と直結したのは明治三〇年で、「貨幣法」によって純金の量目二分(〇・七五グラム)に相当すると定められた。昭和六年(一九三一)の金本位制離脱後は、対ドルあるいは対ポンド相場がその価値の基準となった。第二次大戦中から戦後にかけて円の価値は暴落したが、昭和二四年一ドル三六〇円とされた。昭和三九年日本がIMF八条国になるとともに、円の交換性は回復に向かい、さらに目ざましい経済力の成長から国際的にも、その価値が高まり昭和四六年一二月、一ドル三〇八円と切り上げられた。昭和四八年二月、アメリカがドルの再度の切下げを行なったのを契機に、主要国通貨はいずれも変動相場制に移行し、円もこれにならった。
平面的な円形を表わす「まと」「まとか」に対して「まろ」は本来円筒形や球形を表わしたものという。中世以降「まる」に転ずるとともに、平面、立体ともに意味するようになった。→「まる(丸)」の語誌
日本の貨幣の単位。1871年(明治4)5月、維新政府が制定した「新貨条例」により、日本に流通する貨幣の単位の呼び名が、江戸時代の「両(りょう)」から「円」に改められた。そして流通貨幣を全国的に統一し、金本位制度が採用されることになった。すなわち、(1)純金1500ミリグラムを1円とし、20円、10円、5円、2円、1円の5種の金貨を本位貨幣として鋳造する、(2)円の100分の1を「銭(せん)」、銭の10分の1を「厘(りん)」とし、従来の四進法(1両=4分(ぶ)、1分=4朱(しゅ))を十進法に改める、(3)貨幣を新たに円形とし、前記の本位貨幣のほかに50銭、20銭、10銭、5銭の4種の銀貨、および1銭、半銭、1厘の3種の銅貨を補助貨幣として鋳造する、というものであった。「円」という名称は、貨幣を円形としたこと、日本が鋳造機械を買った香港(ホンコン)で当時すでに円の呼称をもつ貨幣が用いられていたこと、またメキシコから流入してきた円形の銀貨を洋円とよんでいたことなどから、形状と名称の実例に基づいて名づけられたものといわれている。
[原 信]
この新制度は、当時欧米先進国で採用されていた金本位制に倣ったものであったが、東洋の主要国は銀本位制をとっており、また、貿易にはメキシコ銀などの銀貨が主として用いられていたので、貿易の便宜のためとして「貿易銀」と称する1円の銀貨の鋳造が認められていた。これは当初は開港場における通商取引にのみ用いられるものとされていたが、1878年(明治11)に国内一般にも流通せしめるようになり、事実上は金銀複本位制の形をとるようになった。
このような制度の発足にもかかわらず、明治初年来、新政府の発行した多額の不換紙幣や、1877年の西南戦争によるインフレーションで、金・銀貨と紙幣の価値が大きく乖離(かいり)するようになり、金・銀貨は退蔵され、物価上昇はひどくなった。
1881年、松方正義(まさよし)が大蔵卿(きょう)に就任すると、財政緊縮と増税などにより強力な引締め政策を断行、財政の黒字を通じて大量の不換紙幣を回収した。さらに1882年には日本銀行を設立、1884年には兌換(だかん)銀行券条例により、同行は銀貨に兌換できる兌換銀行券発行の特権を認められ、翌年には初めて額面10円の兌換日本銀行券が発行された。かくして、日本は実質的には銀本位制になったが、1890年代になると世界的に銀の価値が金の価値に比して大きく低落するようになり、円は金本位制をとる欧米諸国の諸通貨に対して為替(かわせ)相場が下落し、国内の物価上昇を招いた。
政府はこの事態に対処するため、1893年に貨幣制度調査会を設けて幣制改正の研究を進め、その結果、金本位制への移行が急務との結論に達した。しかし、それには巨額の金準備が必要とされ、着手は困難を極めたが、1897年に日清(にっしん)戦争による清国からの賠償金2億3000万両を得ることとなったので、これをもとに、名実ともに金本位制に移行した。同年制定の貨幣法により、1円を純金750ミリグラム、すなわち従来の半分にし、日本銀行券は金貨に対する兌換券となった。この段階で日本の近代的通貨制度が確立した。
[原 信]
第一次世界大戦中の1917年(大正6)9月、日本はアメリカに続いて金輸出を禁止し、約20年間続いた金本位制を停止した。大戦後、アメリカは1919年、ドイツは1923年、イギリスは1925年、もっとも遅れていたフランスも1928年には金本位制に復帰したが、日本は戦後のインフレーション、およびその後の関東大震災の影響により、復帰は容易にできず、円の相場は下落した。1929年(昭和4)7月に成立した浜口内閣の蔵相井上準之助は、緊縮財政をとるとともに、1930年1月11日には金輸出禁止を解除し、金本位制に復帰した(いわゆる金解禁)。しかし、おりからの世界恐慌のさなかに、当時の円の実勢を20%以上も上回る旧平価(100円=49.846ドル)での金本位制復帰であったため、大量の正貨準備が海外に流出し、国民生活は深刻な影響を被り、翌1931年末には早くも金輸出を再禁止せざるをえなくなった。これにより金本位制は事実上崩壊し、管理通貨制度の色彩が強まることとなった。
その後円相場は急激に下落したが、日本は戦時下の統制経済に移り、1933年には外国為替管理法が公布され、円相場は英ポンドまたは米ドルに対し釘(くぎ)付けされた。日中戦争に突入した1937年以降は、戦費の増大に伴い銀行券の発行高は著増した。これに対応するため1942年2月には日本銀行法が公布され、兌換銀行券条例は廃止となった。これによって、発券制度は、これまでの保証準備屈伸制限制度から最高発行額制限制度に変更となり、また、金輸出再禁止以来停止措置がとられていた金貨兌換も正式に廃止され、日本銀行券は兌換券ではなくなった。ここに管理通貨制度が法的にも確立されたわけである。
[原 信]
第二次世界大戦の敗戦直後の日本は激しいインフレーションにみまわれ、経済再建は困難を極めた。1946年(昭和21)2月17日には金融緊急措置令および日本銀行券預入(よにゅう)令が公布、即日施行され、10円以上(のちに5円以上)の日本銀行券を金融機関に強制的に預け入れさせ、これを既存の預貯金とともに封鎖し、一定の制限のもとに新円への切り換えを行うことによって、銀行券発行額を収縮させた。さらに1949年からは、占領軍のドッジ金融顧問によるドッジ・ラインといわれる超均衡予算政策が遂行された。一方、1947年から制限的ながらも民間貿易が再開されたが、円の対外価値は輸出入別、品目別に多様な相場が適用されていた。しかし1949年4月25日に1ドル=360円という単一為替相場が設定され、それ以後の日本経済の内外発展を基礎づけるものとなった。
これらの施策を通じて、インフレーションもようやく収まり、1952年に国際通貨基金(IMF)に加入、360円を正式の対米ドル平価とし、それから逆算して円の金平価を1円につき0.0024653グラム(1トロイオンス=1万2600円)として登録した。
第二次世界大戦後の復興過程を経て、日本経済は1950年代、1960年代と著しい成長を遂げ、国際競争力を高め、1960年代後半には国際収支の黒字が定着するようになった。一方その間、戦後の国際基軸通貨国たるアメリカの競争力は後退し、大幅な国際収支の赤字を継続、ドル不安を招来し、1971年8月にニクソン大統領はドルの金交換を停止した。この国際通貨情勢の混乱を収拾するため同年12月18日スミソニアン協定が結ばれ、ドルは金平価を7.89%切り下げ、円はドルに対して16.88%切り上げて1ドル=308円とする新しい中心相場が決定された。しかしながら、その後も国際通貨の不安はやまず、1973年2月、アメリカがドルの再度の切下げを行ったのを契機として、主要国通貨はいずれも変動相場制に移行し、円もこれに倣った。
[原 信]
円の対米ドル相場は変動相場移行後、大きな変動を繰り返し、1980年代前半、第二次オイル・ショックの影響やアメリカの高金利を背景に1ドル=250円前後の円安・ドル高の水準で推移したが、そのためアメリカの経常赤字が拡大し、一方、日本や西ドイツ(当時)などの経常黒字が拡大した。
円安・ドル高の不均衡を調整するため、1985年9月の先進5か国財務相・中央銀行総裁会議(G5。1986年からG7)でプラザ合意が成立、ドル高修正のため為替市場介入など協調体制がとられた。その結果円は急上昇し、1987年には150円に達した。同年2月、先進7か国財務相・中央銀行総裁会議(G7)のルーブル合意で、相場維持のための協調体制がとられたが、円の上昇は止まらず、1988年には120円台となった。
1993年初め、アメリカの財務省高官の円高容認の発言などを機に円は新たな上昇段階に入り、同年8月には100円を突破、1995年4月には史上最高の79円に達した。
このような円高により、日本経済は停滞し、緩和された金融政策のもとで、株式や土地価格などの上昇によって資産インフレとなった。それが急激に崩れて、いわゆる「バブルの崩壊」となり、第二次世界大戦後最大の不況を招き、経済構造上も深刻な問題となった。円相場は1ドル=79円をピークとして円安方向に調整され、さらに日本の歴史的低金利(公定歩合0.5%)と金融システムの不安、そして1997年夏に始まった東アジアの通貨危機の影響も加わり、1998年に入ると円安の傾向は強まった。
1980年代の末期から円の対米ドル相場は、おおむね100円から140円の円高基調を続けており、日本は1980年代末より、国内総生産(GDP)の2~3%程度の経常収支黒字を継続している。それが年々蓄積されて、2007年末では日本の対外純資産額は250兆2210億円(1ドル100円として2兆5022億米ドル)で、名目GDPの48%とほぼ半分に匹敵し、世界最大の債権国となっている()。したがって円高の基調は中期的には当然だが、為替相場は短期的には、景気の見通し、株価、金利およびそれ以外の状況をみて、思惑的な資金移動や先物取引などにより、為替相場はつねに不安定である。とくに1991年のソ連崩壊後、金融資本市場の世界的な自由化同質化(グローバリゼーション)が進み、また日本を含めた先進国の低成長を背景とした巨額の余剰資金がヘッジファンドなどを通じて、投機的に活動することもその背景にある。
円相場は、20世紀末の波乱のあと新世紀に入り円高基調に戻るが、日本当局は極端な円高により景気回復が妨げられるのを恐れ、100円の水準を割られないよう強力な円売りドル買いの介入を実施した。2000年の3~4月には約2兆3000億円、2003年の7~9月には7兆5000億円、2004年の1~3月には14兆8000億円とその期間はほとんど連日介入し、また日米の高官のいわゆる口先介入も市場に影響を与えた。しかしその後、介入の効果もあってか相場は不安定ながら円安方向に転じた。
市場は金利や景気動向に敏感に反応し、金利の安い円などを借り、金利の高い通貨の資産に投資をするという「円キャリー取引」(円キャリートレード)といわれる取引が相場を動かすようになった。円は安くなり、オーストラリア・ドルなど高金利通貨は高くなった。もとより為替相場変動のリスクはあるが、高リスク、高リターンという風潮が支配的であった。2005年は継続してじりじりと円安基調で2006年も年央の一時を除いて円安が進み、さらに2007年も年央には120円を超えるまでになった。そこで同年7月世界の金融市場にくすぶっていたサブプライムローン問題が表面化し、アメリカ金融機関の発行した住宅ローンに関連する証券に対する不安感が世界の金融市場に広がり、次々と金融機関の破綻(はたん)やその可能性が伝えられ、かつての世界恐慌以来の危機が始まった。これはまずアメリカ金融システムの危機であり、国際通貨としての米ドルの危機であり、当然米ドル相場は他の主要通貨に対して下落することになる。事実ユーロ、英ポンド、スイス・フランそしてそれまで3年ほど下落の傾向であった円まで米ドルに対して上昇に転じた。ようやくアメリカの対外借金経済のつけが回ってきたと思われ、アメリカ当局も日欧諸国にドル防衛の協調体制についての合意をとりつけたほどであった。
問題はアメリカだけでなかった。ヨーロッパの大きな金融機関もそれぞれ損失を被り、当面のドル債務決済に要するドル資金を必要とし、アメリカ連邦準備制度理事会(FRB)は主要中央銀行とスワップ協定によりドル資金を日欧の市場に供給した。すなわち当面の問題はドル不安よりドル不足であった。2008年9月リーマン・ブラザーズの破綻以降、為替市場はドル高に転換した。
そのなかで円だけは円高が進み、100円を割って90円台に移った。それは、金融危機で、先進国はもとより、期待された新興国も景気後退が予想され、金利も低下し、それまでもっとも不況かつ低金利であった日本が比較的に危機の影響が少なく、経常黒字を継続する強さが見直されたとする見方もある。しかし不況はさらに深刻で円高はそれに拍車をかける。過去の内外の国内インフレ率を比較すると、90円台の円高は決して不当ではないし、経常収支不均衡の是正にも役にたつはずだが、問題は米ドルで、対円以外はドル高の状況では、アメリカの大きな不均衡は是正されず、為替相場は不安定のままで、諸政府の対応いかんでは金融不安は進み、世界恐慌への道をたどる。しかし、かつての経験を踏まえて、諸政府および国際機関が積極的な対策をとりつつあり、世界の生産が半分に落ちるというような結果は避けられよう。ただ米ドル中心の国際通貨体制は当面変わらず、特定国の通貨を国際機軸通貨とする以上、不安定で、ユーロも円もそれに振り回されるような状態はしばらく変わらないだろう。
[原 信]
一方、円の対内価値をみると、明治以来大きい変化があった。1996年(平成8)の円の国内価値は、1934年(昭和9)~1936年に比べ、卸売物価ベースで約700分の1である。しかし第二次世界大戦後は、その終了直後と、二度にわたるオイル・ショック時代のインフレーションの時期を除き、円の国内価値は比較的安定している。1980年以降物価上昇率は年平均1.8%程度であったが、1992年(平成4)以降1%を上回ることはほとんどなく、1995、2000、2001の各年はマイナスであった。21世紀初めの10年は、内需の低迷で物価も低迷の状況であるが、海外情勢や環境問題のほかエネルギー価格や資源価格、穀物価格の影響で、ときに不安定な動きを示している。
[原 信]
日本経済の成長とともに円の国際的地位も向上し、円が公的準備通貨として外国当局に保有される比率は増加し、非居住者の保有する円建資産も増加した。また日本の輸出の円建決済比率も20世紀の末期には35%程度に上昇した。このような背景にたって、政府は1980年に新しい外国為替及び外国貿易管理法(現在の外国為替及び外国貿易法)を施行し、従来原則禁止、要許可とされていた外国為替取引を原則自由とし、とくに資本取引面の制限を大きく緩和した。
円は、アメリカに次ぐ世界第2位の経済大国の通貨として、外国当局の外貨準備や国際投資、国際金融および国際決済に利用されてきた。ひところは英ポンドを上回る地位を占めたが、バブル崩壊後の金融危機や、円高による景気の低迷や超低金利で円の地位は低下し、米ドルやユーロに比べると、その国際性はなおはるかに低い。
外国当局保有の外貨準備のなかで円の比率は6%をピークとして、最近では3%程度に落ちた。世界の為替市場で円が為替取引の相手方になっている比率は16.5%、1日約5000億ドル(米ドルは86.3%、1日約2兆6000億ドル)で、その約8割は米ドルとの取引である。また為替市場としての東京の比率はロンドン、ニューヨークに次いで第3位だが、6%と低く、取引高の約75%は円対米ドルの取引である。
次に、貿易の仕切り通貨および決済通貨として2008年現在では円の利用状況は輸出が約40%、輸入が約20%強で、この10年ほどの間に輸出が若干伸びた程度で、著変はない。輸出では、アジア向けの約半分が円建てであり、ODA(政府開発援助)や円借款が支えとなっている場合もあろう。輸入で注目すべきはヨーロッパ連合(EU)向けの半分が円建てになっていることで、ヨーロッパの輸出国通貨主義が日本に対しても徹底しているとみてよいだろう。しかし一般に輸入では原油や原材料で慣習として米ドルである場合も多く、近い将来比率が高まるという予想はできない。また日本が直接の当事者でない場合、第三国間で円が利用されることはまれである。
円の国際的利用を活発にするには、やはり中国やインドも含めたアジア地域との経常、資本両面の取引拡大で、おのずから利用度が伸びることが望ましい。事実アジア地域での取引決済通貨としての円の比率は前記のように輸出の場合もっとも高く、輸入もEU以外の地域より高い。対アジア貿易額が全貿易額に占める比率は、輸出では1997年の42%から2007年の48%へ、輸入では36%から43%へと増加し、アメリカやEUは減少している。この地域への直接投資の拡大や、1997年および2008年の金融危機に対する国際協調支援体制(たとえば、日本銀行と各中央銀行の間のスワップ協定やアジア通貨基金構想なども含め)の強化その他で円活用の地盤を広げることが必要である。
2009年現在でおもに流通しているのは1万円、5000円、2000円、1000円の日本銀行券と、500円、100円、50円、10円、5円、1円の補助貨幣である。
[原 信]
『吉野俊彦著『円の歴史』(1955・至文堂)』▽『島野卓爾・荒木信義編『円高・円安』(1980・有斐閣)』▽『速水優著『円が尊敬される日』(1995・東洋経済新報社)』▽『上川孝夫・今松英悦編著『円の政治経済学――アジアと世界システム』(1997・同文舘出版)』▽『ロナルド・マッキノン、大野健一著『ドルと円』(1998・日本経済新聞社)』▽『島崎久弥著『通貨危機と円の国際化』(1999・多賀出版)』▽『菊地悠二著『円の国際史』(2000・有斐閣)』▽『谷口智彦著『通貨燃ゆ――円・元・ドル・ユーロの同時代史』(2005・日本経済新聞社)』▽『宮崎義一著『ドルと円』(岩波新書)』▽『鈴木武雄著『円――その履歴と日本経済』(岩波新書)』
平面上で一定点から一定の距離にある点の全体でできる曲線のこと。その定点を円の中心、一定の距離を円の半径、その曲線を円周という。円周のことを円ということもある。このときは円周で囲まれた図形を円板という。円周上の2点を結ぶ線分を弦(げん)といい、とくに円の中心を通る弦を円の直径という()。直径の長さは半径の2倍である。直径の長さに対する円周の長さの比はどの円でも一定で、この値を円周率という。したがって、円周の長さlは、半径をr、円周率をπとすればl=2πrである。また、円の面積SはS=πr2である。
円はその中心に関して点対称であり、どの直径を軸にとっても線対称である。円はこの整った対称性が活用されて、車輪、マンホールの蓋(ふた)、硬貨、円卓など、直線に次いで日常至る所で目に触れる図形である。円の弦によって分けられる円周の二つの部分を円の弧(こ)といい、弦と弧で囲まれる図形を弓形(きゅうけい)という。とくに直径で分けられる図形を半円という。また、中心で直交する二つの直径で分けられる四つの図形をそれぞれ四分円(しぶんえん)という。円の中心を端点とする二つの半直線のなす角を、その半直線でできる弧に対する中心角という。このとき二つの半直線でできる二つの角のうち、小さいほうでできる弧を劣弧(れっこ)、大きいほうでできる弧を優弧といい、この二つの弧を互いに他の共役弧(きょうやくこ)であるという。円周によって平面は円の内部と外部に分けられる。円の内部の2点を結ぶ線分上の点はまた円の内部にあり、内部の点と外部の点を結ぶ線はかならず円周と共有点がある。
円と直線の位置関係は三つある()。円と直線が2点で交わるとき、この直線を円の割線(かっせん)という。円と直線がただ一つの点だけを共有するとき、この直線を円の接線といい、その共有点を接点という。接線は接点を通る直径と直交している。第三の場合は円と直線が共有点をもたない場合である。
二つの円の位置関係は五つの場合がある()。二つの円をA、Bとして、円Aを固定して考える。まず、円Bが円Aの内部にあり、それぞれの円周に共有点がない場合である。とくに中心が一致すれば、二つの円を同心円という。次に円Bが円Aの内部にあってただ一つの点を共有する場合で、円Bは円Aに内接するという。第三は、2円A、Bが2点を共有する場合で、2円は交わるといい、その2点を結ぶ線分を共通弦という。第四の場合は、円Bが円Aの外部にあってただ一つの点を共有する場合で、2円は外接するという。第五の場合は、2円が互いに他の外部にある場合である。第一の場合を除いて2円に共通な接線を引くことができ、その個数はそれぞれの順に1、2、3、4である。
[柴田敏男]
座標平面で、中心の座標が(a, b)、半径がrの円の方程式は
(x-a)2+(y-b)2=r2
である。とくに、中心が原点、半径が1の円を単位円という。
[柴田敏男]
平面上において,1定点から一定の距離にある点全体の作る図形を円と呼び,その定点を円の中心という。円はふつうコンパスを用いて描かれるが,もっと素朴には,伸びない糸の一端を固定して,その周りに他端を回転させることによって得られる。このように,円は簡単に作られるまるくて美しい図形であるので,古くから人々に親しまれた。とくに,合理的な美を理想とした古代ギリシアの哲人たちは円を完全な図形と考え,プラトンなどは直線と円だけで作図できる図形を“幾何学的”とした。ギリシア数学の結晶であるユークリッドの《ストイケイア》でも,円は直線とともに幾何学を構成する基本図形とされている。
円の面積というときのように,円によって囲まれる平面の部分もまた円と呼ばれる。はっきりと区別するため,最初に定義した円を円周といい,円周とそれが囲む平面の部分を合わせた図形を円板という。なお,円の内部,すなわち円板から円周を除いた残りの図形を開円板という。円の中心Oと円周上の1点Pを結ぶ線分OPを半径といい,円周上の2点A,Bを結ぶ線分ABがOを通るとき,線分ABを直径という。半径の長さ,直径の長さもまた同じく半径,直径と呼ばれる。円は直径によって対称な二つの図形に分かれるが,これらを半円と呼ぶ。半径の等しい円は合同で,したがって円の大きさは半径の長さによって定まる。ところで,半径を直接求めるには円の中心を探さねばならないのに対し,直径は円をはさむ平行な2直線間の距離として簡単に測れる。このため古くから円の大きさは半径よりもむしろ直径と結びつけて考えられ,円周の長さの直径の長さに対する比が考察された。この比の値は円の大きさによらない一定の数で,円周率と呼ばれ,ふつうπという文字で表される。πは無理数で,実用的な計算ではその近似値3.14または3.1416が用いられる。半径がrである円の周の長さは2πrで,その面積はπr2である。円周は長さが等しいすべての平面閉曲線のうち最大の面積を囲む(等周問題)。
円周上の2点A,Bを結ぶ線分ABを弦という。円の中心は弦の垂直2等分線上にある。この性質は与えられた円の中心を求めるのに利用できる。すなわち,円周上に3点A,B,Cをとり,弦ABの垂直2等分線と弦BCの垂直2等分線を作れば,それらの交点が中心である(図1)。円の中心を頂点とする角にはさまれた円周の部分を弧といい,はさむ角をその弧の中心角という。半円周は中心角が180度の弧である。円周上の2点A,Bを結ぶ弧を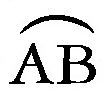 で表す。これは二つあり,一方を他方の共役弧という。A,Bが直径の両端でないときは,共役弧の一方は半円より小さく,他方は半円より大きい。前者を劣弧といい,後者を優弧という。弧
で表す。これは二つあり,一方を他方の共役弧という。A,Bが直径の両端でないときは,共役弧の一方は半円より小さく,他方は半円より大きい。前者を劣弧といい,後者を優弧という。弧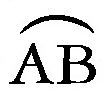 の共役弧の上に点Pをとり,∠APBを弧
の共役弧の上に点Pをとり,∠APBを弧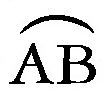 の上の円周角という(図2)。弧
の上の円周角という(図2)。弧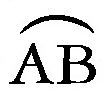 の上の円周角∠APBは,その弧の中心角∠AOBの半分である。したがって,同じ弧の上の円周角はすべて等しく,共役な弧の上の円周角の和は180度である。
の上の円周角∠APBは,その弧の中心角∠AOBの半分である。したがって,同じ弧の上の円周角はすべて等しく,共役な弧の上の円周角の和は180度である。
lを円の載っている平面上の直線とする。円の中心Oからlまでの距離が半径より大きければlは円に交わらず,その距離が半径より小さければlは円周と2点で交わる。後者の場合,lを円の割線という。Oからlまでの距離が半径に等しいときは,lは円と1点で交わるが,この交点をAとするとき,lはAにおいて円に接するといい,lを接線,Aを接点という。Aを接点とする接線lとはAにおいて半径OAに立てた垂線であり,また,それは円周上の点BをAに近づけたときにA,Bを通る割線が近づく直線であるともいえる(図3)。円周上の点Aにおける接線lとAを通る弦ABのなす角は弧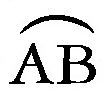 の上の円周角に等しい。円周上にない点Pを通る割線の円周との交点をA,Bとすれば,PA・PBは割線のとり方によらず一定で,Pが円外にあるときは,Pを通る接線の接点をTとするとき,PA・PB=PT2となる。
の上の円周角に等しい。円周上にない点Pを通る割線の円周との交点をA,Bとすれば,PA・PBは割線のとり方によらず一定で,Pが円外にあるときは,Pを通る接線の接点をTとするとき,PA・PB=PT2となる。
同一平面上に半径r,r′の2円があるとき,それらの中心間の距離dと両円周の交点の個数の間に次の関係がある(図4)。|r-r′|<d<r+r′ならば両円周は2点で交わり,d>r+r′またはd<|r-r′|≠0ならば両円周は交わらない。d=r+r′またはd=|r-r′|≠0ならば両円周は1点で交わり,交点における両円の接線は一致する。d=r+r′のとき円は外接するといい,d=|r-r′|≠0のとき両円は内接するという。なお,中心を同じくする2円を同心円という。
平面上に直交座標系をとり,平面上の点を座標を用いて(x,y)のように表すとき,中心が(a,b)で半径がrである円周は方程式(x-a)2+(y-b)2=r2をみたす点(x,y)の全体からなる。この方程式を円の方程式という。この円周上の点(c,d)における接線の方程式は(x-c)(a-c)+(y-d)(b-d)=0である。原点を中心とする半径1の円周を単位円という。これは,複素平面上では絶対値1の複素数eiθ=cosθ+i sinθ(iは虚数単位)の全体として表され,複素数の積により位相群となる。単位円は現代数学においてしばしば基本的役割を演じている。
執筆者:中岡 稔
円は象徴的には,限定された宇宙的空間,生命,循環,中心などを意味する。さらに旧石器時代から太陽の象徴として知られ,ギリシア,インドなどの神話においては,太陽神の持物とされており,天空,光明,永遠,力,調和,統合なども表す。循環する円は,あらゆる動きを示し,統合と分割,再統合,進化と退化,成長と退行,生と死の過程など永遠の時間の象徴として知られている。
ヘレニズム文化の中で考えられ,さらに錬金術で用いられた永遠の時間を表すものに,自分の尾をかむ蛇の図形があり,ウロボロスと呼ばれている。永遠にみずからをのんで成長を繰り返す循環的な時の経過や,原初的混沌(こんとん),またはあらゆるものを包含する一者を表す象徴として知られ,すべての数,または点の総合として,数の10や八角形ともかかわっている。錬金術師たちはこの図形を第一質料から究極的目標に向かう動きの象徴として用いた。ウロボロスには明暗二色に塗り分けられているものもあり,これは中国の周敦頤の考えた陰陽の二極が無限の動きを作りだす太極図に近いもので,それぞれの瞬間における対立するものの統合と調和を意味している。太極は目に見えない宇宙の根源的実在だが,そこから陰陽の二気が生じ,さらにその二気が動くことから,水火木金土の五行が成立し,太極の動きと二気,そして五行の働きによって,男女が生まれ万物が生成するという原理を説明するために考えられた図形である。
1年の12ヵ月を表す図形や占星術の黄道帯も円形で表され,統合・分割・循環を意味するが,さらに中心と四方に広がる内的宇宙と完成を意味するものに,円と四角の組み合わされた図形である曼荼羅がある。曼荼羅は仏教では無上正等覚という最高の悟りの境地を表すもので,心理学者ユングによれば,中心・全体・調和を意味する超越的自己の象徴とされる。
執筆者:秋山 さと子
円は日本貨幣の基本単位名であるが,1871年(明治4)制定の〈新貨条例〉によって採用された。銭・厘を補助単位とする十進法の計算体系をもつ。それまで流通の江戸期金貨には1601年(慶長6)制定の両・分(ぶ)・朱という単位が使用されていた。1両=4分,1分=4朱の四進法であり,鋳貨の形態にも小判形と方形との2種があった。日本の貨幣制度を世界的水準にあわせようとして採用された円銭厘体系の採用により,両分朱の単位は廃止された。
明治政府の鋳貨が円形に統一されているという特徴をもつため,〈円〉という単位名が生まれたというのは俗説である。18世紀から19世紀にかけて中国に流入したドル銀貨=洋銀と呼ばれるスペイン,メキシコの銀貨は,銀塊としての中国固有の銀貨に対し,その形態的特徴から中国では銀円と呼ばれた。これが,イギリス香港(ホンコン)造幣局鋳造(1866-68)の香港ドル銀貨の中国人用極印が〈香港一円〉となった理由である。しかし円の正字〈円〉は画数が多い欠点があり,ために円と同発音で意味も貨幣にふさわしい元が自然的に多用され,他方中国自身も円形銀貨=銀元を鋳造しはじめ,ついに1933年の〈廃両改元令〉によって元が中国貨幣の基本単位名になる。ただし自国貨幣の元と区別するためドルを美元(美とはアメリカの中国名,美国のこと)と表記する。
中国のドル銀貨への対応は幕末日本にも導入された。ただし中国の貨幣名になった元は敬遠され円が多用された。幕末の知識人はもとより庶民一般も,円を流入したメキシコ銀貨に対してのみならず,小判の単位両の別称,さらには両に代わるものとしてさえ使用するようになった。他方,ドル専用の当て字として弗を使用するという幕府官僚のくふうが円からドルの意味を払拭(ふつしよく)したこと,明治政府成立時に円の称呼をもつ貨幣の鋳造が地球上になかったことも円が日本貨幣名となる一因を形成するが,1870年に香港ドル銀貨と同じ品位・量目の銀貨を本位貨幣とする銀本位制度を採用するとの決定がその総仕上げとなる。しかし,この決定直後から視察・調査・研究のために渡米した伊藤博文からの建言により,急きょ金本位制度に改変されることになったが,円はそのまま流用され,〈新貨条例〉による正式採用決定をみる。
補助単位の〈銭〉はアメリカの補助単位セントの発音に類似のために採用されたともいわれているが,これも俗説である。東洋世界での銅銭の原基となった唐の開元通宝(621鋳造)の量目を,宋以降に新たな単位として匁または銭と呼んだ。日本の銅銭,和同開珎も寛永通宝も当初量目が一匁のゆえに,これらを一文銭と呼ぶ。明治政府は補助単位の基本通貨に銅貨をあてることにしたので,中国の故知にならい銭を採用した。〈厘〉は一般度量衡単位から銭の1/10にあたるものとして採用したもの。円のマーク¥はその横文字表記YENのYに由来する。ただし歴史的には〈ゑんWEN〉と表記され,や行の〈え〉ではない。YEN表記は,幕末以降の日本に決定的影響を与えた英語国民が江戸をYedoと書いたように,〈え〉をyeと表記したことや,ヘボンの手になる《和英語林集成》(1867)が〈え・ゑ〉で始まるすべての日本語をye……として表記したことによる英語的表記にしたがうもの。
1871年成立の金本位制度の原貨1円は純金1.5g(=0.4匁)をふくむ。その数値は国際貨幣制度確立案としてアメリカ下院に提案中の1ドル金貨の純分として伊藤がアメリカから建言したものであるが,それが明治政府の鋳造で価値尺度として流通していた二分判2枚=1両の純分量に近似でもあり,新旧物価が1両=1円として連結し物価体系の移行に難のないため,採用されたもの。金本位制度として出発した円にもかかわらず,西欧文化文明摂取のための輸入激増や西南戦争(1877),日清戦争(1894-95)等による不換紙幣・銀行券の濫発と金流出のため金本位制度の維持は至難となり空文化した。82年に設立された日本銀行発行の日本銀行券もやむなく銀兌換にせざるをえなかった。しかし日清戦争によって得た賠償金で97年,〈貨幣法〉の制定により第2次金本位制度が確立され,日銀券も金兌換となる。ただし1円の金平価は750mg(0.2匁)と半減した。
日銀券の金兌換は1917年まで継続されたが,同年に第1次世界大戦による金本位制停止で金輸出禁止とともに兌換も停止された。戦後,世界主要国の趨勢にしたがい日本も30年に金本位制に復帰したものの,世界的不況のあおりをくって31年末には金輸出の再禁止,金兌換の再停止のやむなきにいたった。32年に政府は金買上価格を1匁=7円25銭(1g=1円93銭)と定めた。これは金0.2匁=1円(1匁=5円,1g=1円33銭)と定めた〈貨幣法〉の規定に穴をあけるもので,ここに政府の円の金量保持放棄が公然化され,円価値下落への道がひらかれることとなる。第2次世界大戦遂行のための一策として,金本位制度にかえるべく41年に導入され,翌年に正式採用となった日銀券の最高発行額制限法は円価値下落に拍車をかけた。敗戦によって爆発した悪性インフレーションにもとづく増幅もあって,戦後国際社会に復帰し国際通貨基金(IMF,1952加盟)に通告承認された1円の金平価は2.4685mgにまで減少してしまった。この金平価は,1ドル=360円という円の対ドル為替相場を基準に1ドルの純金分を360で割って算出された。50年代末期以降,ドルの弱体化が顕著になり,ドル危機が続いたが,71年8月,ついにアメリカは正式に金・ドル交換を停止し,金1オンス=38ドルへの引上げ(ドルの切下げ)を行い,1ドル=308円の新しい円の対ドル為替相場が決定された(スミソニアン合意)。これ以降IMF体制が崩壊しはじめ,73年2月に固定為替相場制が変動為替相場制となり,78年に金は通貨の価値基準の役割から排除され,金に自由相場がたつようになった(以上〈国際通貨制度〉の項目参照)。アメリカは85年には71年ぶりの純債務国に転落した。一方日本は,1968年から純債権国へと歩み出した。アメリカは貿易黒字によって経済力の強化を図るため,為替レートをドルの実勢に一致させるべく85年9月に開催した主要5ヵ国(G5)の会議でのプラザ合意(会場になったホテル名に由来)により,ドル高・円安の是正に踏み切った。しかしその貿易収支への効果は希薄であったのに対し,円高・ドル安は急速に進行し,88年1月には1ドル=120円45銭を記録し,94年6月には100円を突破したが,97年には120円前後で安定している。金の市場価格1g=1321円(1997年平均)として,1円は金0.757mg相当となる。円はその誕生時の金量の約1/2000にまでやせ細る苦難の歴史をたどったのである。
→貨幣
執筆者:三上 隆三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

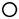 で示したもので、員がその初文。のち員を他義に用いるに及んで、更に外周を加え、圓となった。〔説文〕六下に「圜(ゑん)の
で示したもので、員がその初文。のち員を他義に用いるに及んで、更に外周を加え、圓となった。〔説文〕六下に「圜(ゑん)の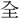 きものなり」とし、「讀みて員の
きものなり」とし、「讀みて員の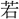 (ごと)くす」とする。
(ごと)くす」とする。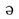 n、圜hiuan、丸huanは声義近く、みな、まろきものの、円周、円転の意がある。宛iuan、腕uan、爰hiuanも同系の語とみてよい。
n、圜hiuan、丸huanは声義近く、みな、まろきものの、円周、円転の意がある。宛iuan、腕uan、爰hiuanも同系の語とみてよい。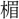 ▶・円方▶・円満▶・円夢▶・円門▶・円融▶・円麗▶・円顱▶
▶・円方▶・円満▶・円夢▶・円門▶・円融▶・円麗▶・円顱▶出典 平凡社「普及版 字通」普及版 字通について 情報
出典 株式会社平凡社百科事典マイペディアについて 情報
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
明治期以降の通貨の基本単位。1871年(明治4)の新貨条例で純金1.5gを1円(さらに十進法で銭・厘)と定めたが,中国で円・元とよばれた1ドル銀貨とほぼ等価だった。1円金貨は1両とほぼ等価で交換されたが,銀価下落にともなって海外流出が多く,85年には銀本位制度に移行した。97年貨幣法で純金0.75gを1円とする金本位制が確立したが,1931年(昭和6)の金輸出再禁止以後対外価値は大きく下落した。第2次大戦後の49年に1ドル=360円の固定相場が設定されたが,71年の308円への改訂をへて73年から変動相場制に移行,ドル下落にともなって円高が進んだ。
出典 山川出版社「山川 日本史小辞典 改訂新版」山川 日本史小辞典 改訂新版について 情報
…すなわち63年に福田恒存,芥川比呂志らが文学座を脱退し,〈現代演劇協会〉を設立,その付属劇団として〈雲〉(正式名称〈劇団雲〉)を創立し,拠点劇場としての〈三百人劇場〉(東京千石)も建設した。しかし両者はさらに決別し,三百人劇場に拠る福田恒存らの〈昴(すばる)〉と,75年に脱退した芥川比呂志,岸田今日子,仲谷昇らの〈円〉(正式名称は〈演劇集団円〉)に分かれた。また俳優座,民芸でも数多くの脱退者を出した。…
…古語ではモチヒと呼称しており,モチイヒ(糯飯ないし黐飯)の約語と解釈したり,鏡餅を典型とした円形状の食物であるから望月の望と同意とする説もある。いずれにせよ,もち米を蒸して臼に入れ,杵で搗(つ)いたうえで,いろいろの形につくったものを餅の字で表してきたのであるが,餅という漢字は日本独自の使い方であり,中国の用法とはまったく異なっている。…
… 図形としては,次のようなものが用いられる。点(それ以上凝縮しえない究極的相を示す),直線(成長・展開の相を示す),円(〈全体〉を表す),四角形(自然の質料を表す),三角形(サーンキヤ学派の説く純質・激質・暗質という自然の三つの性質などを示し,下向きのものは女性原理を,上向きのものは男性原理を表す),下向きと上向きの二つの三角形が交わってできる六芒星の形(六角の星形で,現象世界を顕現させる力を表す),五芒星(地・水・火・風・空の〈五大〉などを表す)などである。そのほかに〈門〉を表す形(聖域に入る入口を示す),蓮の花弁の形(神格の属性としての願望を成就させる力などを表す)なども用いられる。…
…円形ないしそれに近い多角形プランの部屋,または建物のこと。多くはドーム状の天井や屋根をもつ。…
※「円」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
〘 名詞 〙 春の季節がもうすぐそこまで来ていること。《 季語・冬 》 〔俳諧・俳諧四季部類(1780)〕[初出の実例]「盆栽の橙黄なり春隣〈守水老〉」(出典:春夏秋冬‐冬(1903)〈河東碧梧桐・高...