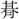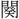〈かず〉ともいう。数学で単に数という場合,複素数を意味するが,もっと狭く,実数に限定した意味に用いられることもよくある。おおまかに分類すれば次のようになる。

また代数的数の概念に関連して次の分類もある。

また実数の分類には次の二つもある。

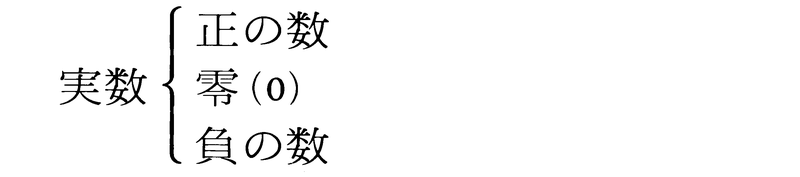
数概念の発達
数概念の出発は,個数を数えることから自然数の概念に到達することであり,いろいろな古代文明において,その段階には到達していた。次の段階は正の分数であるが,この発展については地域による差が大きかった。中国ではずいぶん古くから自然数の十進法による表記法が整い,掛算の九九も整っていて,分数も〈何分之何〉という言い方で,われわれと同様な理解をしていた(九九という語は,古代中国の九九の表が〈九九八十一〉から始まっていたことによる)。古代メソポタミアでは六十進法を利用していて,分数ではなく,六十進法の有限小数を扱っていた。古代エジプトでは,十進法を使っていたが,分数については単位分数(自然数分の1の形の分数)を使い,一つの分数を表すのに,同一の単位分数を複数回使うことを避けるという不思議なことをしていた。よく引き合いに出されるものに,2/29を表すのに,1/24,1/58,1/174,1/232の和としている記録(2/(2n+1),(n=1,2,……,50)を単位分数の和に換算する表が古文書にあり,その中の一つ)がある。ギリシア数学に影響を及ぼしたピタゴラス(前6世紀)は,分数概念をはっきりもっていたと信じられている。このように,紀元前の時代に分数概念がはっきりしていた文明は少ないようである。
上記の古代文明のいずれについても,大きい数から小さい数を引く減法は知っていたが,中国以外では負の数の導入はされていなかった。中国における負の数の導入は3世紀に劉徽によって注釈の書かれた《九章算術》ではすでに行われている(中国数学)。7世紀にインドで負の数の導入がなされ,それがアラビアへ8世紀ころ伝わり,その後ヨーロッパへ伝わったのが12世紀ころといわれている。無理数についていえば,面積に関して開平,体積に関して開立,直角に関して三平方の定理はいずれもある程度古代中国でも古代ヨーロッパでも知られていたようであるが,近似値には着目しても,無理数概念の確立には至っていなかった。とくにヨーロッパでは,三平方の定理に関連して,ピタゴラスは\(\sqrt{2}\)という無理数の存在を知ったが,当時線分の長さは,それに含まれる点の数に比例するという信仰があり,\(\sqrt{2}\)が分数で表せないことの意味がわからなくて苦しんだという。〈ゼノンのパラドックス〉(二つあり,一つはアキレウスはカメを追いぬくことができない,他は矢は飛ばないというもの)も,上記信仰に対するパラドックスであるという。ユークリッド(エウクレイデス)が整数でない実数をあまり扱わず,整数と図形とに力を注いだのも,ピタゴラスと同じ悩みをもち,それに明確な答えが得られなかったからであるという説もある。いずれにしても,有理数でない数の存在を知りながら深入りは避けて,無理数概念をはっきりさせずに近世まできてしまったようである。16世紀になってヨーロッパの数学が急速な発達を始め,17世紀になってG.ライプニッツらにより無限や連続が意識されるようになり,19世紀になって,A.L.コーシー,J.W.デデキント,G.カントルらによって実数概念が確立されたのであり,これは解析学の発展と密接な関連がある。他方,三次方程式の解法に関連して,G.カルダーノが負の数の平方根を利用したのが虚数の導入の最初であるが,数として導入したのでなく,計算の補助手段としての利用であった。虚数と実数を併せたものを数として扱うようになったのは18世紀末ころからであり,先駆的人物がL.オイラー,最重要人物がC.F.ガウスである。
以上の発展をふりかえると,数概念の発展には,(1)除法を可能にするための正の分数の導入,(2)減法を可能にするための負の数の導入というように,四則演算の要請による数の拡張,(3)開平,開立など,べき根という概念による拡張,(4)計算の補助手段としての虚数の導入,(5)解析学の発展に伴う実数概念の確立,さらなる数学の発展に伴う複素数概念の確立という段階を経たといえよう。
大小関係
自然数には大小関係があるから,正の分数\(\frac{n}{m}\) と\(\frac{n′}{m′}\)とについては,分母を払ったm′nとmn′との大小によって自然に大小関係が入る。他方,引算が(正の範囲で)可能なものの積について,
(a-b)(c-d)=ac+bd-bc-ad
であることから,負の数の導入に際して,
(-x)y=x(-y)=-(xy),
(-x)(-y)=xy
と定めた。このことから,有理数全体に大小関係が入り,次の条件を満たす。
(1)a≧b,c≧d⇒a+c≧b+d
(2)a>b⇒-a<-b
(3)a>0,b>0⇒ab>0,したがって
a>0,b>c⇒ab>ac
実数が収束有理数列の極限であることから,実数にも大小関係が入り,上の(1),(2),(3)を満たす。しかし,複素数の範囲では(2),(3)を満たすような大小関係は存在しない。理由は,(2),(3)が成り立てば,〈x≠0⇒x2>0〉が得られるのに,虚数単位iをとればi2=-1<0となるからである。
→数学
執筆者:永田 雅宜
数と世界観
数の概念は自然数の発見以後,それぞれの文化的環境のもとにいろいろに発展してきた。ここでは,その一つである世界観と関連した分野について述べることにする。
単数あるいは1は数概念の基本であるが,世界観との関係では2が基本となる。2は1に1を加えたものには違いないが,一方で2は対として1組という性格ももっている。さまざまな言語,とくに古代語の名詞において,単数,複数のほかに双数または両数dualという形をもつものがあり,多くはしだいに複数形に吸収されてしまうが,これらは単に1足す1としての2ではなく,〈対〉としての2が起源ではなかったかと考えられる。対となるものは私たちのまわりにはいくらでもある。男と女,夜と昼,月と太陽,冷と熱,雨期(湿)と乾期(乾),白と黒,前と後,上と下,左と右,さらには悪魔と神,善と悪,美と醜といった対も存在する。このような対概念は2からなると同時にその二つで一つのまとまりをもっている。このことが双分的世界観の基本となる性格である。まとまりのある世界はこのような対からなるとする双分観は実は世界各地に広く分布しており,これは本来的に人間がもつ基本的な認識類型の一つと考えられる。それゆえ,単なる双分観ではなく双分的世界観と呼ぶものは,極度にさまざまな現象が対概念として結びつけられている世界観ないしは宇宙観(コスモロジー)に限定すべきであろう。この双分的世界観の特徴は,世界の中心をもたない点である。ここにおいては,すべての物や現象は両極に分離している。分離してバランスをとっているといってもよい。例えば,乾と湿のバランスの上に作物が実るし,冷と熱のバランスで人間は健康でいられる。
このような中心不在の世界観には双分観のほかに四分観,八分観と呼ばれる世界観がある。前者は対概念を二つ組み合わせて4要素とし,この四つの要素によって世界が成立しているとみる世界観である。典型的なものは4方位に関係づけられた世界観である。一方,八分観はきわめてまれなものであるが,原理的には四分観の4要素がさらに二分された8要素からなると考える世界観である。中心不在の考え方として,蛇-カエル-ナメクジのような〈三すくみ〉のようなものもあるが世界観としては存在しないようである。三すくみも三分観の一つであるが,ふつう三分観は中心存在型の世界観として登場する。左右というのは1対の概念ではあるが中心点が存在するという点では三つで1組となる。同様に前後,上下などもその中心点が考えられる。三分観は双分観に中心という要素を加えたものといえる。実のところ,先のさまざまの対概念にもう一つの要素を加えることができる。例えば男女の対して中性的な老人が中心点に,太陽を中心として月と星,天国と地獄の間にこの世があるというぐあいである。三分観は典型的には社会体制によくみられる。例えば,王の左右の大臣,王国を中心とした二つの属国というような王国の編成原理がそれである。中心存在型では三分観よりも五分観のほうがより一般的である。五分観は四分観に中心を加えたものである。この五分観がより一般的であるのは人体をモデルとしているからであろう。頭を中心とし両手両足という五つの要素をモデルとしている。典型的には東部インドネシアの5村連合にみられる。中心となる一つの村と他の四つの村が組み合わされて一つのまとまりをもっている。王国ならば,1人の王と4人の大臣によって国が治められている。ここでは往々にして他の村の併合が起きるが,その際,3村連合が他の3村連合を併合すると6村連合とはならず,5村連合となる。1村は他の村に併呑されるか,他の村々に分散されてしまう。
五分観には今一つたいせつなモデルがある。曼荼羅(まんだら)的五分観である。曼荼羅はインドに発したものであり,インドから北方にはチベットへ,南方にはジャワ,バリにまでその影響がみられる。ジャワやバリでは4方位と中心点が重要であり,この五つの要素と神や色,曜日,金属などさまざまなものが関係づけられている。人体モデルと異なる点は中心は頭ではなく,まさに空間的,時間的に中心となることである。例えば,中心となる村はまさに空間的な中心に存在している。
このように森羅万象を2,3,4,5,8のような要素に分解し,そして再編成するという世界観はそれほど多いわけではない。しかし,このような数的世界観は人間文化の基層部にかなり普遍的にみられるものである。とくに双分観や人体モデルとしての五分観はそうである。とはいえ,多くの世界観はこれらの数的世界観のみではなく他のさまざまの世界観と組み合わされ,より複雑な,またよりあいまいな世界観を構成している。その意味では数的世界観は一つのシンプルな世界観といえるであろう。なお,前項〈数〉(言語学)および〈数詞〉の項を参照されたい。
執筆者:吉田 集而
数のシンボリズム
数には物を量的に規定する記号としての役割だけでなく,古代から呪力や象徴的機能が認められ,数占いや暗号術といった特殊な技術の成立にまで至っている。その源泉は太陽,月,5惑星などにみられる自然における周期性,宗教上の理念,また数自体の数学的性質などに求め得る。例えば7が神秘な数とされるのは,月齢周期の1/4に一致する事実に加え,10までの自然数のうち最大の素数であり,分割しがたく計算上も取り扱いにくいという性質に由来するといわれる。宇宙は数により支配されるとしたピタゴラス学派は,1から4までの4自然数とその合計である10を図形化したテトラクテュスtetraktysを神聖視した。彼らは創造と終末,生と死を一巡する存在の単位を10と考え,また数の力を具体化させた音楽によって病気の治療をも試みたという。ユダヤでは腹に9の字を書いて腹痛を鎮めたといわれ,日本においても1から10までの数を唱えて病気治療を行った話が《先代旧事本紀》にみえる。さらにプラトンはピタゴラスおよびピタゴラス学派と同様に,数を調和の本質とし,宇宙を形成する元素を数の面からとらえた。〈プラトンの正多面体〉,または〈プラトン立体〉と呼ばれる五つの正多面体(正四面体,正六面体,正八面体,正十二面体,正二十面体)はそのような思想の反映と考えられ,後世ケプラーの宇宙モデルにも採られている。また古代オリエントでは六十進法が作られ12を基本とするヨーロッパの数の文化を育て,ヘブライの伝統では文字と数とを同記号で表現することによって数の象徴的意味が拡大され,ゲマトリアなどの神秘的な解読術も生まれた。中国や日本でも数は卜占的な意味をもち,漢字の字画などとも関連して考えられてきた。またアフリカ,南太平洋地域,南北アメリカの未開民族もそれぞれに複雑な数のシンボル体系を所有する。以下は各地域,各民族の間ではぐくまれてきた数の象徴的意味の代表例である。
0は一般に非存在を意味するが,すでにその中にあらゆるものの存在を暗示する場合が多い。全体,混沌,永遠,循環,生と死などを含み,しばしば蛇が自分の尾をかむ象徴的図形(ギリシア,ヘレニズム文化圏ではウロボロスとよばれたもの),あるいはそのバリエーションで表される。
1は存在の始まりであり,精神,点,中心,楽園,神,光,超越者,陰陽の陽,父,男性,積極性などを意味する。1は2を生むものとして統合的な数ともいえるが,奇数として偶数と,存在として非存在と対立するので,完全な統合の数ではない。
2は反映,葛藤,線,角,主と客,男性と女性,両性具有などを表す。また1との関係で陰陽の陰,生むものとしての母,第二の性としての女性,受動性などのほか,善悪,生死,異同などの二元的対立を媒介するものとしてのエロスなどを表す。
3は誕生,新生,対立する原理の調和,具象,3点を結ぶ三角形で形の始まり,統合の中の成長の芽を表し,力動的な変化の数とされている。キリスト教では三位一体,キリストの生誕を祝福する東方の三博士の参拝などにみられるように聖なる数であり,中国では天・地・人の三才を示す。昔話や伝説には,三つのなぞ,3個の箱,三つの願い,3人の姉妹または兄弟などの主題がよくみられ,呪術的で神秘的なものごとの達成,失敗,転換とかかわる。
4は四つの方向(4方位),四つの風,四季,自然,大地,キリスト教では楽園エデンから流れ出る四つの大河,四福音書,十字架の四辺などを表し,ギリシアでは全体性を表現する最小の数であった。地水火風の四元または四大は宇宙を構成する原理であり,それに対応して四つの体液が想定されたことから人間の性格や心理機能も四分割されて考えられることが多い。2組の対として,調和,平衡の意味もある。しかし日本では〈死〉と通じるので不吉な数とされている。
5は人間の両手両足と頭,5本の指,五感など,また身体的健康や愛,物質の本体,プラトン主義では美の精髄として考えられた。また古代・中世では四大以外の元質で,万象に拡充する第五元素quinta essentiaであり,中国では四分割の中心,または四点の統合を表す貴重な数として陰陽五行説の基礎を成した。天を意味する3と大地の2を足した数として聖なる結婚を意味することもあり,五角形または五芒星形pentagramとして魔よけに用いられた。4の完成から一歩を進めた発展,春の生気なども意味する。
6は二つの三角形の結合で,両価性と平衡の数。人間の魂や両性具有を意味することもある。火と水の結合,結婚,処女性,秤,キリスト教では天地創造の終りを示す完成の数である。これは6が完全数であることに由来するともいわれる。
7は奇跡,秘宝などを意味し,世界の七不思議,七色の虹など神秘的な数とされている。3と4を足した一種の完全性を意味することもあり,7層の天,1週の7日などものごとの基本単位を表している。
8は八角形が円に近い多角形であることから,完全,統合,円環,対立の統合,自然と精神の合体による再生を意味し,8の形からヘルメスのもつ杖である2匹の蛇のからんだカドゥケウスと結びつけて考えられた。そこから無限に上昇する数として永遠を指す記号とされた。中世のキリスト教ではふつう八角形をしている洗礼盤に関連して洗礼の水を意味し,東洋でも無限,無尽蔵,多数を指す数である。
9は3の3倍で,天界,地界,冥界の三つの世界を支配する完全な力を意味する。ヘブライの伝統では真実を意味し,中世の儀礼では体・知性・精神の一致として優越性を表した。日本では〈苦〉に通じるので縁起の悪い数とされているが,他の東洋諸国では一般に幸運の数として知られている。
10は十進法の基本で統合の数。1,2,3,4を足した数として4とかかわる。洋の東西を問わず,宇宙全体を統合的に表現した完全なる数として知られる。
11は移行,余剰,受難などを意味するが,1と1が並ぶ形から2と同義に考えられることもある。
12は宇宙的秩序を表す。占星術の黄道十二宮,東洋では十二支(干支)など,空間と時間,円や輪の動きと関係して回帰や循環も意味する。
13はキリスト教ではとくに災厄の数(13日の金曜日など)とされているが死と再生の象徴でもある。
執筆者:秋山 さと子+荒俣 宏
聖数
聖数の由来と諸例
先に述べられた数の象徴的意味に基づいて吉凶を占う習慣は全世界の民族にみられる。このうち縁起のよい数を聖数,悪い数を忌数(いみかず)と呼び,たいていの場合偶数か奇数かが区別の重要な基準となる。奇数を尊んだピタゴラス学派は,二分割して神(1)の残らぬ偶数を空虚な数とみなした。またユングは,一般に奇数が崇拝される理由に計算時の手ごわさを挙げ,奇数計算をこなせる者に特別な権威が与えられたとする。したがって奇数には男性的勢威と創造力とが認められる。すなわちギリシアでは生命をつかさどる神アポロンやディオニュソスの祭礼を7と9の日に行ったといい,バビロニアでは13,15,17の各日が神殿の棟木を立てるのに吉なる日とされた。当時の地中海世界では7ヵ月か9ヵ月で生まれる新生児は成長し,8ヵ月で生まれた子は死ぬと信じられたし,ヒッポクラテスも胎児が3ヵ月後に母胎で動きだせば男児,4ヵ月後なら女児と考えた。インドの習俗に,不妊の女性が7種の井戸から集めた水を浴びて懐妊を願うのも,奇数の男性的力によっている。この7は,エジプトでは7惑星,メソポタミアでは7日ごとに変化する月の相の象徴であり,〈幸運数〉として尊ばれた。これを継承したユダヤ教では,神が6日間で世界を創造した後の第7日目を安息日とする1週間の生活リズムにこの数を導入した。このように,聖数は自然現象や生活実態とによく一致し密接感をもつことを特長とする。他方,偶数にもそうした密接感は多数存在し,聖なる偶数を作りだしている。例えば4は4方を,6は4方に上下を加えた大地を象徴する聖数である。北アメリカのインディアンは4にすぐれた神秘力を見いだし4方位とそこから吹く風の創造力に根拠を求める。西洋には四大の思想があり,世界を構成する四元素に超自然力を認めている。また日本では〈多〉を意味する8,すなわち4の2倍が,おそらく八卦などの中国的聖数観が流入するのと前後して聖数となったらしく,後述のように8のついた名称が頻出する。さらにハワイで族長を〈八つ目の人〉と呼ぶように,ポリネシアでも8を聖数とする地域は多い。
一方,聖数と忌数を区別する基準にもっと論理的で抽象的な考え方を適用する動きもある。例えば7について,ライプニッツはこれを二進法で111と表現し,宇宙の三界が無(0)から有(1)に変じた様を示すから《創世記》の神の創造日と合致するとした。しかし歴史的に重要なのは,前述のピタゴラス学派の教義で,彼らはもっとも神聖な数を1,2,3,4とその合計数10であるとした。宇宙の調和美を象徴する協和音がオクターブ(2:1),4度(4:3),5度(3:2)によって生ずる事実が,これを裏づけているのだという。彼らは他に〈友愛数〉〈完全数〉などの概念について先駆的研究を行い,例えば完全数については1000までの自然数の中に3個しかみつからないことから,世間に数少ない〈美徳〉の数として崇拝したという。最初の女性数2と男性数3の結合した5を〈結婚数〉と名づけ神聖視したのも彼らである。1から9までの数を並べたとき中央に位置する5は,ルネサンス以降も〈中央数〉と呼ばれ,国家の中心に君臨する王の象徴に用いられた。一方,9はギリシアをはじめ古代ケルト,ゲルマン文化圏において極大を示す聖数であり,最大限の力を発揮させる目的から軍団の単位人数に採用された。今日のスポーツに9人制が多いのはこれのなごりとする説もある。このように自然現象や生活実態,数学的理念によって生じた聖数には,世界的に意味をほぼ同じくするという一種の普遍性が伴う。これに対し,各民族で意味を異にする聖数も多いが,これらには別種の成立事情が考えられる。第1は数と語呂合せの関係であろう。日本の聖数の代表8が弥栄(いやさか)の弥(や)に通じ,逆に忌数4と9が〈死〉と〈苦〉に発音を同じくするなどがその例である。またヨーロッパではギリシアとユダヤで発達した文字と数字の置換法(ゲマトリア)が使われた。例えば《創世記》にアブラムが神に祝福されてアブラハムと改名したとあるのは,創出の聖数5を得るためにH(ヘブライ文字では5番目)を加えたと解釈される。
このほか,聖数にはジンクスや因縁に基づくものもあり,これによった聖数は当然ながら普遍性をもたない。例えばラッキーセブンlucky sevenは1930年代に大リーグのサンフランシスコ・ジャイアンツが何度も7回に逆転劇を演じたことに由来し,偶然のできごとからの転用である。ただ,本来7には幸運数の意味があったため世界に広まったのであろう。また忌数13はキリストが使徒とともに13人で行った〈最後の晩餐〉に起源がある。以来,キリスト教圏ではパーティや集会に13人で卓を占めることが忌みきらわれ,ホテルの部屋や航空機の座席に13号を作らない。アメリカにはとくに13を忌む人が多く,大統領F.D.ローズベルトなどは着席者が13人になると重要な会議にも秘書を席に加えたという。ただし1ドル紙幣のデザインに13段のピラミッド,13個の星,13本の矢というように忌数があふれているのは,独立時に13州あった事情による。しかし一方では13を聖数とみる民族も少なくなく,オーストラリア北部の土着民は朝日の射しだす光線の数を13として崇拝する。
執筆者:荒俣 宏
中国の聖数思考
古代世界では,数は抽象的思考の産物ではなく,何らかの実体的性格のあるものと観念されていた。いわば数は物として扱われたのである。そこで数の観念が発達して,数の性質を発見していくようになると,ある性質をもった数を聖数とみなし,これに特別の意味と価値を与えるようになる。このことをとくに主張するのはヨーロッパの研究者であって,とりわけ神話の中に認められる数の事例から,各民族に固有の聖数を見いだしてくるのであるが,神話が断片的にしか残されていない中国にあっては,この作業はきわめて困難である。中国の聖数を考える場合,思想的な洗練を経て定式化された数の体系の中から聖数を導き出さねばならない。そのうえ聖数という観念は伝統的な中国の学問では問題にされることがなく,事例の検証が十分でない現状で,聖数に迫るには,論理的な推論を加えるほかはない。例えば,M.ウェーバーは中国的な宇宙創成論を論じて,五星,五行,五臓等々の中に大宇宙と小宇宙の対応関係を見いだし,5という聖数を主張したし,天は丸く地は方(四角)であると考えた古代中国人の蓋天説的宇宙観から4に特別な意味を与えるヨーロッパの研究者もいる。
この4ないし5を聖数とみる考え方は,古代中国社会に照らすとき,ある種の妥当性をもつ。いまは彼らの空間分割の観念を例にとってこれを推定してみる。殷人は殷の地を中商ないし中土,四囲の地を東土,南土,西土,北土と呼び,四つの方位を東方,南方,西方,北方と呼んだ。ここでいう方は,単に方位を意味するだけでなく殷に服属しない異民族を指すことばでもあるのだから,殷人の観念では,空間は4ないし5に分割されていたのである。中央に位置する殷を除いて四分割された空間は,さらに二分ないし三分することにより細分化されていくが,とくに重要なのは8である。8は《周易》という占いの書物で体系化された八卦を意識させるほか,中州を中心に中国を九つの地域に分ける九州説に展開していく。中国人は地上における空間分割をまた天に投影して天を区分したのである。前2世紀ころの漢代では,天は北極を中心に,そこからの距離が36度の圏内にある決して沈まない星座を中官(ないしは中宮),その外側を囲み季節によって見え隠れする星座を外官(外宮)とし,外官をさらに四分割するのである。《史記》の東宮,南宮,西宮,北宮,のちの東方宿,南方宿,西方宿,北方宿がそれである。天の4方を二分割しこれに中官を加えれば九分野になる。しかも天のある分野に起こる現象は,地上のある州に起こる現象と対応するという分野説を生み,占星術の基礎を開くことになる。また天が9層に分割されているという《楚辞》に認められるような伝承の存在は,北アジアのシャマニズムで9を聖数としたという理解に連なる。
さて,4空間を三分割すれば12になるが,これは殷に起源する十二支を意識させるほか,漢代以降盛んとなる十二分野説,十三州説と連なるのである。地上の観念が天上に投影されるだけでなく,地下にもそれは及ぶ。例えば漢代の緯書《河図括地象》や晋の張華の《博物志》では,大地の四隅にそそりたつ柱が天を支えるように,地下の四隅の柱が地を支え,さらに3600本の軸が幽都を囲むような地下構造を作っているという。3600は4を900分割した数である。中国古代に4方あるいは5方という方位観念が存在することはわかったが,他に6方という観念もある。これは4方に天地の2方を加えた方位,つまり5方の中に天地の2方を重ねる方位である。この三次元空間を象徴化した祭祀用具が《儀礼》観礼にみえる方明で,観礼とは天子が諸侯に謁見する儀礼をさす。謁見は宮と呼ばれる4壁に囲まれ4門を開いた場所で行われ,中央に三重の壇を設ける。最下壇は12尋(1尋は8尺),最上壇に方明を置く。方明は木で作った1辺が4尺の正六面体で,各面は6色に塗り分けられている。東方が青,南方が赤,西方が白,北方が黒,上方が玄,下方が黄である。鄭玄(じようげん)の注によれば,6色は6方の神の象徴で,天子はまず方明に祭祀を行い,方明に納めてから諸侯に謁見するのであるが,諸侯と盟約するときはあらためて方明を壇上に置くという。この6方の中に世界が包含されるのであって,6はまた《周易》の六爻(こう)を連想させる。いまもし地下の方位にまで観念が及べば,当然7方になるはずであるが,こうした観念は古代の中国社会には存在しなかった。しかし,北アジアのシャマニズムでは9層の天のほかに7層の天を想定していたという議論もあり,七夕伝説や北斗七星信仰の存在と併せて7を聖数とみるむきもある。
以上,殷人に始まる空間の四分割,五分割ないし六分割の観念を通して,中国の古代人が4に特別な意味を付与している事実を指摘し,5,6,9などはそこから副次的に意味づけされた数と認め,だいたんにそれが聖数化していく過程を推論した。それを神話の世界に立ちいって証明することはいまだなしえていないし,一方では,7あるいは9を聖数とみる観念もシャマニズムの世界には存在していたらしく,それも先にみたように空間分割との関連でとらえうるのであって,4,5,6と7,9との関連なども今後の研究にまたねばならない。なお,4は四方風や四神に神格化されて,その後の中国人の信仰を集め,5,6は春秋から戦国時代にかけて体系化されて,陰陽説,五行説として展開していく(陰陽五行説)。
執筆者:勝村 哲也
日本における数の民俗
陰陽思想では奇数を陽数として尊び偶数を陰数としてきらうが,日本にも8世紀初めの記紀編纂(へんさん)のころにはこの大陸風の考え方が伝わっていたらしい。この考え方は今日では贈答品に4,6,8など偶数をきらい奇数を喜ぶ風習として定着しているが,一方,厄年などはむしろ奇数が多く,一概に論ずることはむずかしい。古代日本の場合,記紀神話の中では中国の易で少陽や老陽としてもっとも尊ばれた7や9はさほど重視されておらず,むしろ10以下ではこのほかの数,とりわけ8が聖数とされていた。例えば,八尋殿(やひろどの),大八洲(おおやしま),八衢(やちまた),八咫烏(やたがらす),八岐大蛇(やまたのおろち),八百万神(やおよろずのかみ)など数が多いことを表すほかに神聖な数とみられていたらしい。8だけでなく,3や5も三世界(高天原,黄泉(よみ)国,現(うつし)国)や三種の神器,イザナミ・イザナキの三貴子,宗像(むなかた)の三女神,五魂(海,川,山,木,草),五十猛(いそたける)神,五部(いつとも)神などの例があり,吉数とみられていた。しかし,《日本書紀》あたりからしだいに大陸文化を尊ぶ風が盛んになって,七夕(7月7日)や重陽(9月9日)の節供のように8に代わって7や9が聖数として重視されるようになり,今日では七五三,三三九度,お九日をはじめとして民俗のうえでは欠くことのできない重要な数となっている。
数は民俗の中では,俗信における語呂合せなどに基づく不定のものと,年中行事や人生儀礼での期日,供物の数,行為の回数,年齢など一定しているものとがある。前者の代表は四=死や九=苦をきらう例だが,ほかにも四九=死苦,六三=無産,七九=泣く,八六=病む,八九=厄,一八一八=いやいや,四九八九=四苦八苦などがあり,これらは商売する人にはきらわれ,電話番号も縁起のよい数を選ぶ。毎年の国家予算や受験番号も,その数字を縁起のよい語呂合せで読んで幸運を願ったり安心したりする。また6月4日を虫歯のムシと解し虫歯予防デーとしたり,同様に3月3日を耳の日,8月7日を鼻の日にしたのも語呂合せである。
数は単なる記号や数える道具ではなく,そこにある霊的なものが宿るとする数霊信仰も民俗の中に認めることができる。数詞を語呂合せで解釈するのもその一例だが,民俗儀礼における供物の数や行為の回数,さらに昔話や夢などの想像的な世界での数にはそれが強くうかがえる。例えば3はある意味で〈満つ,充つ〉に通じ,御三家とか三大原則など充足しためでたい数とされており,人生儀礼でも出産や婚礼では3は儀礼上重要なくぎりの数とされている。沖縄では火の神は三つの石で表象されオミツモンと呼ばれて尊ばれている。また昔話の中では,三郎や三吉など主人公の名まえや,三人兄弟とか三度の繰返しなどといった形で3が頻出する。しかし一方で,3は忌数ともなり,3人並んで写真をとると真ん中の人が死ぬとか,三軒長屋の真ん中の家はたたりがあるといわれる。これらは友引に葬式を出さないとか忌負けなどと同様の風習かも知れない。とにかく数のもつ吉凶は状況により変化するといえるようである。7にも聖数と忌数の両方の性質があり,とくに人生儀礼では生と死,此の世と異界などの移行の儀礼の際に重視されている。7は七福神,七賢人,七珍万宝,七支刀,七曜剣などという反面で,七難八苦,七転八倒,七去,七曲,七化(ななばけ),七変化(しちへんげ),七里結界(けつぱい),七不思議,七人ミサキなどということばがある。また七草,七所祝い,お七夜,初七日,七五三,七つ祝い,七庚申,七墓詣など民俗儀礼ではたいせつな数とされている。
一般に厄年や年祝は精神的肉体的に人生の節目の年齢であり,新旧の世代の移行がなされるため,とくに厄年は影の暗い側面が強く表出しているが,逆に祭礼で厄年の人が神役につく例も多い。厄年は女子は3,7,9のつく数,男子は2,5のつく数とされるが,女子の場合13歳,19歳,33歳,男子の場合は25歳,42歳というのが代表的なものである。また長寿を祝う年祝には,還暦(61),古希(70),喜寿(77),米寿(88)などがある。
10をこえた数では12,13,33,49,100,1000などが重用される。12は1年の月数であり,しかも3と4をかけた聖数であって暮れのミタマノメシのように供物の数としてしばしば用いられるほか,山の神を十二様とか十二山の神とよぶ地方もある。13は日本では十三仏,十三塚,十三参りなど信仰上の重要な数であり,十三(じゆうそう)という地名も各地に分布している。33は厄年や弔い上げの年忌とされ,49も忌明け,七七日(なななのか),四十九餅など葬送儀礼でよく使われる。100は百日目の食初めとか百度参りといった儀礼や祈願にみられ,1000も千社詣,千社札,千人針,千人結び,千歳飴(ちとせあめ)など縁起のよい数とされている。
執筆者:飯島 吉晴
 〈スウ〉
〈スウ〉 〈ス〉かず。「
〈ス〉かず。「 〈かず〉「
〈かず〉「 [名]
[名] [接頭]名詞に付いて、粗末な、ありふれた、安価な、などの意を表す。「
[接頭]名詞に付いて、粗末な、ありふれた、安価な、などの意を表す。「





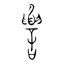

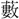 ・籔の二字を収める。
・籔の二字を収める。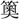 (すいいく)で、といだ米をあげるざる。その編みかたが、乱れ髪に似ているのであろう。ゆえに字は數に従う。
(すいいく)で、といだ米をあげるざる。その編みかたが、乱れ髪に似ているのであろう。ゆえに字は數に従う。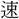 (速)siokは急疾、數をその意に通用することがある。
(速)siokは急疾、數をその意に通用することがある。