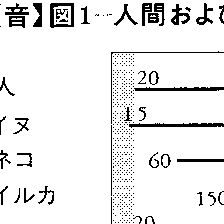
目次 音の研究の歴史と音の利用 音圧と音圧レベル 音の発生 音圧波形 音の伝搬 騒音 ふつうには,空気中の縦波でその振動数(周波数)がおよそ20Hzから2万Hzの範囲にあって,人間がその耳で知覚できるものを音ということが多いが,人間の耳に聞こえるのは一般的な意味での音のごく一部分にすぎない。耳に聞こえるといっても,人間以外の動物の可聴振動数範囲は,人間のそれとは必ずしも同じではない(図1)。コウモリ が自分から出した音波を利用して,暗やみの中でも障害物などの存在を感知することはよく知られている。この場合の音は人間の耳には聞こえない超音波 領域にあるが,これも広い意味での音に含まれる。また20Hz以下の振動数の音を超低周波音 infrasoundと呼んでいる。この超低周波音はやはり人間の耳には聞こえない音であるが,ふつうの騒音と違った形で環境問題の一つになっている。このように空気中だけでも,人間の耳に聞こえるのは非常に限られた範囲の音であるが(ただし,ここで述べているのは定常音についてであって,非定常音では5万Hz程度まで知覚できるといわれる),さらに液体や固体の中を伝わる弾性波には多くの種類がある。水など液体の中では,空気中と同様に縦波だけが存在するが,固体中では縦波のほかに横波もできる。地震波も地下の深いところで,何かの原因で発生した弾性波が,地中や地表面を伝わるものである。縦波や横波など波の種類によって,伝搬速度など波動の性質もさまざまであるが,こうした弾性波も一般的な意味では音である。このように音あるいは音波は,波動を伝える媒質や振動数などについて,本来,非常に広い範囲の現象に使われるものであるが,ここでは空気中の音で,とくに人間の耳に聞こえる周波数範囲の音を中心にして記述し,広い意味での音については〈音波 〉の項目を参照されたい。
音の研究の歴史と音の利用 人間にとって,音は音声による情報,意志の伝達手段として非常に重要な役割を果たしてきた。また音楽としての音に対する関心は,人間の歴史とともにあったと考えられる。前500年ごろにピタゴラス が行った弦の振動や音階についての研究は,音響学 のみでなく広く自然科学の数学的取扱いの出発点になったといわれている。その後,楽器や劇場,音楽堂などの音の問題は,つねに多くの人の関心の対象になってきたが,音の物理的性質についての研究が自然科学の一分野として系統的な発展を始めたのはガリレイ の時代からである。その後,17~19世紀にかけて,M.メルセンヌ,ニュートン ,ラプラス ,ヘルムホルツ,レーリー らが,力学の問題として音波を取り扱ってきた。その集大成は1877年に初版が出版されたレーリーの著書《The Theory of Sound》であって,音の物理的性質の研究は,19世紀の後半に基本的な部分の完成をみたということができる。一方,音を人間の耳に聞こえる範囲で考えるときには,聴覚の機構が重要な問題になる。音による空気の圧力変化が耳に到達すると,これによって鼓膜が振動し,これは耳小骨を経て内耳の蝸牛(かぎゆう)に伝えられる。そしてコルチ器官においてコード化された電気信号に変換され,聴覚神経を通って大脳に伝えられて音の感覚を生ずる。こうした聴覚の生理については,19世紀におけるA.コルチ,ヘルムホルツらの研究に始まり,20世紀になってG.vonベケシーらの業績によって,ほぼその全容が明らかにされている。
20世紀における電気・電子技術の発達は,音についての実験的な研究や技術的な応用に画期的な変化をもたらした。とくに音の物理的な性質と聴覚あるいは音の心理作用などを総合した形での技術の進歩が著しい。電話,録音,放送などの技術は,マイクロホン ,スピーカー ,送受話器など電気音響変換器の発達に裏づけられたものである。またオーディトリアム,スタジオなどでの音の聞こえ方の問題,住宅など各種建築物内での音の環境やさらに一般的な騒音環境の問題には,技術面と並んで心理的な音の評価が重要な役割を果たしている。電気補聴器の開発は,聴覚障害者(難聴者)に音の世界を開いたという点で大きな意義をもっている。人間の音声の性状についての研究も,音響学の重要な一分野になっており,最近では電算機や各種機械の音声制御や音声タイプライター などが,現実のものになりつつある。音響設計 →聴覚
音圧と音圧レベル 音が存在するとき,空気は進行方向に沿って往復運動をしており,この状態が空気中を伝搬する(図2-a)。このように媒質の振動方向が伝搬の方向に一致するような波動を縦波という。図2-bで空気が密になったところは圧力が上昇し,反対に疎になったところの圧力は低下する。すなわち,音が存在する場所の圧力は,音がないときの圧力を中心にして上下に変化する。こうした圧力の変化部分を音圧という。音圧は時間t とともに変化するので,ある時間間隔T をとり,各瞬間瞬間の音圧をp (t )として,ふつうその実効値パスカル (記号Pa)が使われる。聴覚は音圧による鼓膜の振動が原因になるので,音の表示には音圧が基本量として使われるが,そのほかに空気の運動そのものを表す粒子速度が使われることもある。一般に耳に聞こえる音の大小は音圧に左右され,音圧の大きい音ほど大きく感ずる。耳で聞くことのできる最小の音圧は20μPa程度であり,一方,ジェットエンジン の近傍では2×103 Pa程度の音圧になるが,この程度になると聴力障害を起こすおそれがあるので,通常は20μPaから200Pa程度の音圧範囲を音といっている。この範囲は50億分の1気圧から500分の1気圧に相当するもので,人間の耳に聞こえる範囲の音圧が,非常に小さい圧力であることを示し,同時にまた,人間の耳が圧力センサーとして非常に鋭敏であることを意味している。工学の分野では,音圧p の代りにL =20 log1 0 (p /p 0 )で与えられる音圧レベルが使われている。ここでp 0 は基準音圧で,p 0 =20μPaとする。音圧レベルの単位はdB(デシベル )である。このように音圧の対数表示が使われるのは,人間の感覚が刺激の対数に比例するというウェーバーの法則 によるものである。なお,音の大きさを感覚量として表す場合には,ホン という単位が用いられる。
音の発生 音の発生源となるものには,各種スピーカーや楽器のように音を聞くためにつくられているものから,機械類などのように騒音の発生源となるもの,あるいは人間などの発声器官に至るまで非常に多くの種類があるが,音の発生機構としては比較的少数のグループに区分される。
ふつうのスピーカーや弦楽器,打楽器の場合には,まず板や弦や膜が振動し,これに接した空気がそれに応じて運動し,ある条件のときに空気の圧縮膨張を生ずる。そしてこの空気の圧力変化が音波として周囲に伝搬する。こうした物体の振動を起こす原因としては,衝撃力,摩擦力,非平衡力などの機械的駆動力や,電磁力など非常に多くの種類がある。外から振動的な力が加えられているときの振動を強制振動 といい,これに対して,外力をとり除いたあとでの振動が自由振動 である。自由振動の状態は,物体の形状寸法と弾性的な性質によって決まる特定の振動数と振動の状態をもった固有振動 によって規定される。固有振動の数は無限に多く,その組合せによって自由振動の状態が決まる。また強制振動の場合にも,外力の振動数に応じたいくつかの固有振動によって,振動の状態が決まるものである。このように,固有振動は物体の振動に関して,基本的に重要な性質である。
振動する物体から発生する音の性質には,振動の状態などが関係するので,一般的には非常に複雑になる。振動と音との関係を示す例として,半径a の球が周波数f ,振動速度v で全面同位相の状態で振動しているとき,球から単位時間に放射される音の全エネルギー は図3のようになる。すなわち,半径a や振動数f が小さいと,振動をしても音にはなりにくいことを示している。一般に音の高低は振動数に関係し,低い音ほど振動数が小さい。低音用スピーカーには大口径が使われたり,バイオリン に比べてコントラバス の胴が非常に大きいのは,こうした理由によるものである。
音の発生機構としてもう一つ重要なのは,物体の振動にはよらないで,空気自身の一部分に起こった変動によるものがある。強い風のとき電線からヒューヒューという音がでるのは,空気の流れが障害物にあたると,その背後の部分に乱れを生じそこから音が発生するためである。高圧の気体が狭い隙間や穴から吹き出すときの音も同じものである。送風機,圧縮機やジェットエンジンなどの音もこれに含まれる。風や高圧気体による音は,一般に周期がない変動であるので,広い振動数範囲にわたる成分をもった音である。ただ気体の流れが一様であれば規則正しい渦(カルマン渦 )が発生し,そのときの音は,振動数f =0.2v /d (v は気体の速度,d は障害物の直径)に主要な成分をもつ音になる。これをエオルス音 という。
音圧波形 発生した音の音圧の波形(音圧波形)は,発生源の性状によってさまざまな形をとる。いくつかの例を図4に示す。図4-aは正弦音波 または純音と呼ばれる音の波形で,一つの振動数で構成されている。実際の音には厳密な意味での純音はほとんどなく,図4-b以下のような複雑な波形をもつのがふつうである。このうちb,cは整数倍の振動数をもったいくつかの純音の組合せになる。このように多くの純音の組合せでできる音を複合音,それぞれの純音を,その成分または部分音という。部分音のうちで振動数のもっとも低いものを基本音,それ以上の振動数の部分音を順次,第1上音,第2上音,……という。とくにこの例のように上音の振動数がすべて基本音の振動数の整数倍であるときには,第2倍音,第3倍音,……という。また実在する音には,図4-dのように音圧波形が不規則に変化し,同じ波形を繰り返さない音が多い。この場合には,すべての振動数にわたって連続的に成分をもった音になる。バイオリンの音とピアノの音は,たとえ同じ音圧,振動数であっても異なって聞こえるが,これはそれぞれの音圧波形の差異によるものであって,このような音の性質は音色 と呼ばれる。
音の伝搬 空気中に発生した音は,一定の速度で伝搬する。静止した空気中での音速c (m/s)は温度に関係し,t ℃のときc =331.5+0.6t で与えられる。ふつうには15℃のときの値,c =340m/sが使われることが多い(音速 )。周囲に障害物がまったくない開放空間に小さな音源があるとき,これから発生した音はすべての方向に均等に伝搬し,音源を中心にした任意の球面上の音圧は一定になる。こうした音波を球面波という。この場合に球面の単位面積 を通過する音のエネルギーは,音源から離れるに従って距離の2乗に逆比例して減少する。音圧レベルでいえば,距離が2倍になるごとに6dBの割合で低下することになる。これは音の伝搬における重要な法則である。実際には,屋外では,地面はもちろん建物や地形など各種の障害物によって,音の伝搬はさまざまな影響をうける。音が境界面や障害物にあたると,そこで反射,散乱あるいは回折など波動としての各種現象が起こる。また反射面の性状によっては,入射した音のエネルギーの一部が吸収される。反射,散乱,回折などの性状は,障害物などの寸法と音の波長との関係で決まる。可聴範囲の音の波長は1.7cmから17mの間にある。これは人間,自動車,建物などの寸法と同程度であって,そのために障害物の陰の部分にも回折によって音が伝わることになる。また発生した音が純音成分を含むときには,障害物や地面からの反射音との干渉によって,音圧の大きな場所や小さな場所が現れるようになる。
屋外での音の伝搬,とくに遠距離への伝搬については,こうしたいくつかの波動現象のほかに気象条件,すなわち温度分布や風が大きな影響をもっている。ふつう,地表面からの高さに従って大気の温度が低くなるので,音速は高いところほど小さく,音は上方に曲がるような形で伝搬する。これに対して夜間などには高いところほど温度が高くなることがあり,このときには上空ほど音速が大きくなって音は下方に曲がり,遠くまで伝搬する。次に風があるときには,風下方向には音速が大きく,風上方向には音速が小さくなり,しかも一般に風速は上空ほど大きいので,音は風上へは上方に曲がり,風下へは下方に曲がりながら伝搬する。ふつうには,こうした風速や風向,温度分布は時間とともに不規則に変動するので,音源から遠く離れた位置での音圧は不規則な揺らぎを示す。
室内など閉じた空間で発生した音は,境界面で何回も反射を繰り返しながら伝搬するので,室内での音の状態は一般に非常に複雑になる。こうした室内の音場の基礎になるのは,室内の空気についての固有振動の性質である。もっとも簡単な一次元音場として,両端を閉じた細長い管を考えると,この場合の固有振動の振動数f は,管の長さをl としたとき,f =nc /(2l )(n は正の整数)となる。実際の室は三次元の空間であるため,固有振動数および各固有振動における音圧分布はより複雑になる。また室の天井,壁,床など境界面や器具などの表面では,入射した音のエネルギーの一部が吸収されるので,その程度によって音圧の分布も変化する。とくに境界面が綿や連続気泡性樹脂などの多孔質材料 でできていると,材料内部に入った音が隙間内部の表面での摩擦によってエネルギーの多くの部分を失うことになる。こうした材料を吸音材料と呼んで,音の調整に広く使われている。
騒音 音は,音声などの信号による情報の伝達,音楽などさまざまな形で人間の生活に役だっているが,その反面では機械,車両,航空機などから発生した音が,騒音として人間に関与している。非常に大きな音圧レベルの音は,聴力障害の原因となるので人間の環境として望ましくないのは当然であるが,それほど大きな音でなくても,会話やラジオ,テレビの聴取を妨害したり,睡眠や休息,各種の活動に影響を与えることがあり,重要な環境問題になっている。音の物理的性質を表示するためには,音圧あるいは音圧レベルを使うことができるが,騒音の評価量としては,音に対する人間の生理的あるいは心理的な反応とよい相関をもっていることが必要である。騒音の要因の一つは,音が大きいということであるので,人間の感ずる音の大きさに対応するような周波数補正を行った音圧レベルを騒音レベルと呼んで,騒音評価の基本量として使われている。騒音 子安 勝
 〈オン〉
〈オン〉 〈イン〉
〈イン〉 〈おと〉「足音・
〈おと〉「足音・ 〈ね〉「音色/遠音・初音・
〈ね〉「音色/遠音・初音・ [名]
[名] [接尾]助数詞。
[接尾]助数詞。

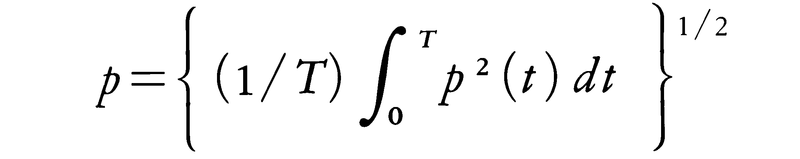
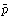 であるとき
であるとき
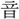

 る、之れを
る、之れを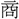 角
角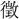 (ち)
(ち)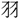 は聲なり。絲竹金石匏土革木は
は聲なり。絲竹金石匏土革木は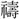 の器を示す
の器を示す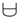 (さい)の中に、神の応答を示す一を加えた形。神はその音を以て神の訪れを示した。器の自鳴を示す意である。
(さい)の中に、神の応答を示す一を加えた形。神はその音を以て神の訪れを示した。器の自鳴を示す意である。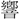 (響)・
(響)・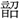 ・
・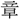 (章)・
(章)・ など五字を属する。
など五字を属する。 彰)を示す字。字形の上で、
彰)を示す字。字形の上で、 ・
・ ・
・ (暗)・
(暗)・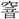 ・
・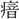 ・
・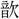 ・
・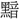 ・闇など十五字を収める。おおむね幽暗にして声を発しない意がある。神が音を以て神意を示す意を承ける。
・闇など十五字を収める。おおむね幽暗にして声を発しない意がある。神が音を以て神意を示す意を承ける。 mは同声。
mは同声。 ・奄iamは覆う。
・奄iamは覆う。
 音・響音・玉音・琴音・空音・恵音・瓊音・古音・鼓音・五音・呉音・語音・弘音・好音・高音・細音・子音・至音・嗜音・嗣音・字音・商音・鐘音・信音・新音・声音・清音・噪音・騒音・促音・大音・託音・濁音・知音・潮音・聴音・底音・土音・同音・徳音・南音・巴音・爆音・八音・発音・撥音・悲音・美音・微音・表音・浮音・風音・福音・母音・方音・法音・北音・無音・余音・拗音・抑音・綸音・櫓音・弄音・録音・和音
音・響音・玉音・琴音・空音・恵音・瓊音・古音・鼓音・五音・呉音・語音・弘音・好音・高音・細音・子音・至音・嗜音・嗣音・字音・商音・鐘音・信音・新音・声音・清音・噪音・騒音・促音・大音・託音・濁音・知音・潮音・聴音・底音・土音・同音・徳音・南音・巴音・爆音・八音・発音・撥音・悲音・美音・微音・表音・浮音・風音・福音・母音・方音・法音・北音・無音・余音・拗音・抑音・綸音・櫓音・弄音・録音・和音