電磁波の一種。狭義には目に見える電磁波,すなわち可視光を意味する。電磁波は波長(とくに真空中の波長)や振動数によって分類されるが,可視光は約810nmから380nmまでの波長範囲,振動数でいえば4×1014~8×1014Hz程度の電磁波であり,この範囲で波長が短くなるに従い,赤,だいだい,黄,緑,青,あい,紫の順に色がついて見える(ただし,目に見える波長範囲や色の感覚は観測者によって個人差がある)。可視光より波長の長い側は赤外線,短い側は紫外線である。これらを含め,一般に波長1mmから1nmくらいまでの電磁波を広い意味で光と呼んでいる。
光の科学
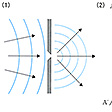
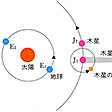
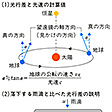
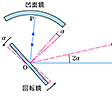
光は干渉,回折やドップラー効果など,波動として特徴的な現象を示し,また,その波長より広い空間で直進し,異なる媒質との境界で一部が反射され,残りは境界で屈折して透過する。光は,進行方向に垂直な面内で,相互に直交した電場と磁場とが同じ位相で振動する横波である。電場の振動面が一方向に限られているものを直線偏光といい,これに対して通常の光源の光はいろいろな方向の振動面をもった光が多数集まったもので,このような光は自然光と呼ばれる(偏光)。光が真空中を伝わる速さを光速度といい,物理学で重要な基本定数の一つであって,とくに相対性理論や電磁気学において重要な意味をもっている。O.レーメルやJ.ブラッドリーが地球の公転を利用して星からくる光の速さを求めたのを先駆けとして,19世紀にはA.H.L.フィゾーの回転歯車を利用した測定が行われ,さらにA.A.マイケルソンによる精密測定によって光速度の不変性が確かめられた。現在では光速度の値として,
c0=2.99792458(1.2)×108m/s
が得られているが((1.2)は下端の桁の誤差),これは一つのレーザーの発する光の波長λ0と振動数νとを測定し,c0=λ0νなる関係を使って求められたものである。
さて,光は波動であるが,その振動数をν,真空中の波長をλ0としたとき,物質との相互作用の際に,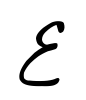 =hνのエネルギーと,向きが光の進行方向で大きさがp=h/λ0の運動量をもつ粒子としてふるまい(hはプランク定数),この粒子をフォトン(光子)と呼ぶ。
=hνのエネルギーと,向きが光の進行方向で大きさがp=h/λ0の運動量をもつ粒子としてふるまい(hはプランク定数),この粒子をフォトン(光子)と呼ぶ。
波動としての光
光学の歴史は古く,古代ギリシアのユークリッド(エウクレイデス)は光が直進することや反射の法則について記述を残しているが,光学が近代的学問としての装いを整えるようになるのはさまざまな光学器械が登場する16世紀以降のことであり,また,これに伴って,光の本性をめぐっての論争も活発化する。
→光学
波動説の確立
ニュートンはプリズムを使った観察から,白色光が多数の色の異なる光に分けられることを見いだし,光の微粒子とこれに刺激されて振動する媒質(エーテル)というモデルを考えて光学現象を説明しようとした。ただしニュートンは光の粒子説をかならずしも積極的に主張したわけではない。ニュートン自身の築いた力学で,力の加わらない質点は与えられた初速度の等速直線運動をするが,光が直進することをこのことに結びつけて説明しようとしたのである。
当時,光を波動と考えたのはC.ホイヘンスやR.フックであった。フックは薄膜が色づいて見える現象が粒子説では説明できないことを示し,光をエーテルの振動と考えた。ホイヘンスは光の速さが有限であること,交差する光が互いに妨げ合わないことから光を媒質を伝わる波とみなしたのであり,彼の波動説の本質は,〈媒質中に波動の源を囲む任意の閉曲面を考え,波がこの面上に到達すると,その各点が新しい波動の源となって球面波を送り出す。この閉曲面の外側の点における振動は,その点でのこれら球面波の重ね合せとして与えられる〉というホイヘンスの原理に示されている。ホイヘンスの原理は,光が直進すること,反射の法則,伝わる速さの異なる二つの媒質の境界で波動が屈折することを説明できたが,当時はニュートンの権威が学会を支配しており,粒子説のほうが主流であった。
波動説が復活を遂げるのは19世紀に入ってからである。まず,19世紀の早々,T.ヤングは二つのスリットを用いた実験によって,光が干渉することを示し,光が波動であることを主張した。ヤングの考えはすぐには受け入れられなかったものの,やがてA.J.フレネルはヤングの干渉実験をホイヘンスの原理と結びつけて,回折は波面上のすべての点から出る波動の干渉によって生ずるものとし,この考えを推し進めることによって,波動説の基礎を確立した(1818)。彼の理論はホイヘンスの原理に数学的な証明を与え,光の直進,回折などの現象を波動説によって完全に説明するものであった。色偏光や複屈折についてはすぐには説明できなかったが,これも光を横波と考えれば理解できることがフレネルによって示された(1821)。そして1850年,J.B.L.フーコーが,波動説から得られる帰結どおり,水中の光の速さが空気中よりも遅くなることを実験によって明らかにし,波動説に確定的な証拠を与えたのである。
電磁波としての光
光が何の波動であるかを予言したのはJ.C.マクスウェルである。彼は,電磁気現象を包括的に記述する基礎方程式,マクスウェルの方程式を提出したが,その最大の特徴は,伝導電流のほかに,磁場を生ずる原因として時間的に変化する電場,すなわち変位電流の概念を導入したことにあった。彼はこれから理論的に電磁波が存在しうることを明らかにするとともに,理論から導かれるその伝搬速度が当時実測されていた光の速度と一致することから,光と電磁波とが同じものであるとの結論に達したのである。電磁波の存在はH.R.ヘルツの実験によって実証され,さらに光と電磁波の性質が同じであることも明らかにされて,光の電磁波説が確立された。
電磁波である光は,二つの電荷の間に働く電気的なクーロン力の場と,二つの電流の間に働く磁気的な力の場の組合せである。一方の電荷や電流から他方へ,力は瞬間的に働くのではなく,距離が大きければ,力が及ぶまでにはそれだけの時間を要する。つまり力の伝わる速さは有限で,その速さが光速度である。電荷や電流は真空を隔てて力を及ぼしあうことができるから,光も真空中を伝わる。その伝わり方は次のように説明される。ある場所の磁場に時間的な変化が生じたとすると,このときまわりの空間には電磁誘導によりこの磁場の時間変化を打ち消すための電流を流そうとする電場が誘起される。この電場は時間変化があるので変位電流であり,これはまわりの空間に磁場を作る。この磁場には時間変化があるのでまた電場を作るというように,この繰返しにより光が空間を伝わるのである。このため,光は時間変化のある電場と磁場との組,つまり振動する電場Eと磁場Hとにより構成され,真空中における電場の大きさEと磁場の大きさHとの比(これを放射インピーダンスという)は,真空の透磁率,誘電率をそれぞれμ0,ε0として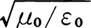 となり,また光速度c0は,
となり,また光速度c0は,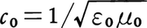 で与えられる。光の強度はエネルギー密度と光速度との積であり,振幅である電場あるいは磁場の大きさの2乗に比例する。これは,単位時間に単位面積を通過する光子数にhνを乗じたものに等しい。またS=E×Hで定義されるベクトルSをポインティングベクトルといい,Sの方向が光の進行方向,その大きさが光の強度を与える。透磁率と誘電率とがμとεとである物質中では,放射インピーダンスは
で与えられる。光の強度はエネルギー密度と光速度との積であり,振幅である電場あるいは磁場の大きさの2乗に比例する。これは,単位時間に単位面積を通過する光子数にhνを乗じたものに等しい。またS=E×Hで定義されるベクトルSをポインティングベクトルといい,Sの方向が光の進行方向,その大きさが光の強度を与える。透磁率と誘電率とがμとεとである物質中では,放射インピーダンスは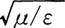 光の速さは
光の速さは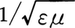 となるが,光の振動数はきわめて大きいので,通常の物質ではμ=μ0としてよく,
となるが,光の振動数はきわめて大きいので,通常の物質ではμ=μ0としてよく,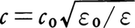 と表せる(ただし,この場合εは光の振動数に依存すると考えなければならない)。
と表せる(ただし,この場合εは光の振動数に依存すると考えなければならない)。
屈折と反射
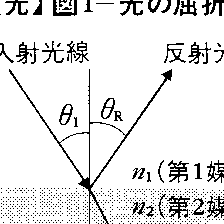
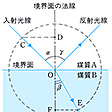
均質で透明な二つの媒質の境界面が波長より広い範囲でなめらかな場合,第1の媒質から第2の媒質へ向かって光が入射し,その一部は第1媒質中へ反射され,残りは第2媒質中へ透過したとする。このとき,透過光の進行方向が入射光の進行方向からかたよる現象が屈折である。波長より広い空間では光は直進するからこれを直線で表すことにし(これを光線という),それぞれ入射光線,反射光線および屈折光線という。このとき,反射光線と屈折光線とはいずれも入射光線と入射点における境界面の法線とを含む面(入射面という)のなかにあり,かつ法線に関して入射光線の反対側にある(図1)。入射光線,反射光線,屈折光線が入射点において境界面の法線となす角θI,θR,θDをそれぞれ入射角,反射角,屈折角と呼ぶが,θR=θIであり,またsinθI/sinθD=n21は入射角によらず一定となる。後者の関係はスネルの法則と呼ばれ,n21を第2媒質の第1媒質に対する相対屈折率と呼ぶ。第1媒質が真空である場合,第2媒質の真空に対する屈折率を絶対屈折率,または単に屈折率という。相対屈折率は第2媒質中の光の速さと第1媒質中のそれとの比の逆数であり,屈折率nはその媒質中の光の速さcと真空中の光速度c0を用いて,n=c0/cで表される。さらに前述のように,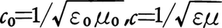 またほとんどの場合μ0=μとしてよいことから,
またほとんどの場合μ0=μとしてよいことから,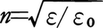 で与えられることになる。ただしこのnの値は光の振動数によって変化し,とくに気体の場合,分極率との関係はローレンツ=ローレンツの式で与えられる。第1媒質中の光の速さが第2媒質中に比べて遅い,すなわちn21<1のとき,入射角θIがsinθI=n21を満たす臨界角を超えると,入射光はすべて反射されるようになる。これを全反射という。異方性のある媒質の屈折率は,その中を伝わる光の電場の方向に依存し,一定入射角の入射光も,その偏光方向によって屈折角が異なり,一般には屈折して二つの光線に分かれる。この現象を複屈折という。対称性の低い結晶や,等方性の物質でも歪がある場合など複屈折が起こる。
で与えられることになる。ただしこのnの値は光の振動数によって変化し,とくに気体の場合,分極率との関係はローレンツ=ローレンツの式で与えられる。第1媒質中の光の速さが第2媒質中に比べて遅い,すなわちn21<1のとき,入射角θIがsinθI=n21を満たす臨界角を超えると,入射光はすべて反射されるようになる。これを全反射という。異方性のある媒質の屈折率は,その中を伝わる光の電場の方向に依存し,一定入射角の入射光も,その偏光方向によって屈折角が異なり,一般には屈折して二つの光線に分かれる。この現象を複屈折という。対称性の低い結晶や,等方性の物質でも歪がある場合など複屈折が起こる。
スネルの法則は入射光に対する反射光と屈折光との位相の関係が,境界面上の位置や時刻によって変わらないことを保証する。第2媒質中に光の波を励起する源は境界面における振動であるから,境界面に時間変化がないとき,屈折光の振動数は入射光と同じで,屈折率nの媒質中の波長はλ0/nである。反射光や屈折光と入射光との間の振幅と位相の関係は,第1媒質と第2媒質との放射インピーダンスの比で決まり,入射光,反射光および屈折光の電場の大きさをそれぞれEI,ERおよびEDとするとき,それらの間にフレネル係数と呼ばれる次の関係が成立する(ただし,第1媒質および第2媒質の透磁率μ1,μ2が,μ1=μ2=μ0とみなせる場合)。
(1)光の電場が入射面に垂直な場合(このような光をs偏光という),
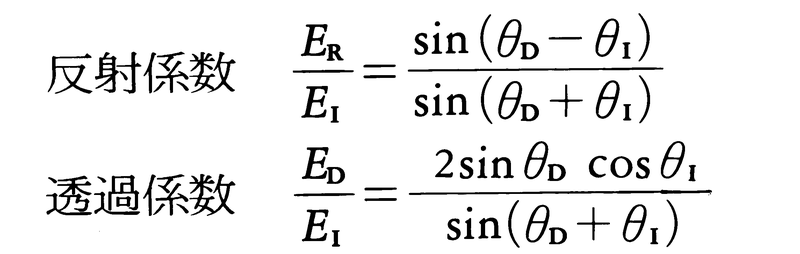
(2)光の電場が入射面に平行な場合(p偏光という),
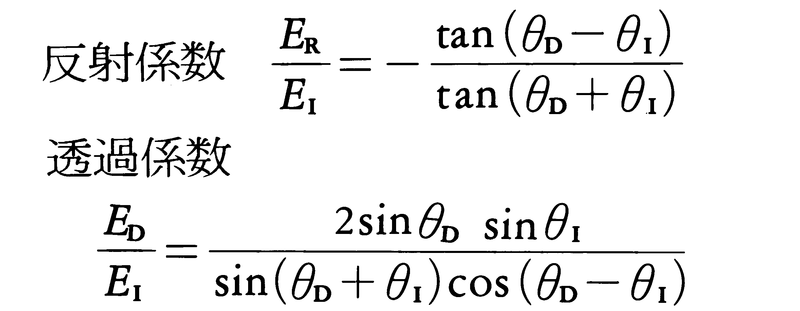
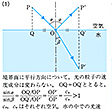
これからわかるように,θD+θI=π/2が満たされるとき,電場が入射面に平行なp偏光の反射係数は0,いいかえればp偏光は反射されない。これはtanθI=n21なる入射角で起こり,この角をブルースター角という。自然光をこの角で入射すれば,反射光は電場が入射面に垂直な直線偏光(s偏光)のみとなる。全反射のときには反射係数は絶対値が1の複素数である。これは反射の際の位相の跳びを与え,s偏光とp偏光とでは,同じ入射角でも,位相の跳びに相違がある。ガラスと空気との境界面で,入射面に対してπ/4だけ傾いた直線偏光は適当な入射角のとき,2回の全反射で円偏光となる。
干渉
二つ以上の波動が同時に1点で出合うとき,その強度が個々の波動の強度の和とならない現象を干渉という。光は振動数が大きく,振幅や位相を直接に観察することはできないが,2乗検波器を用いると振幅の2乗に比例した光の強度を測ることができる。同一振動数の二つの光の振幅を偏光方向を含めてE1とE2とするとき,重ね合わせた光の強度は,E12+E22+2E1・E2cosδ21となる。ここでδ21を二つの光の位相差という。二つの光の振幅と偏光方向とが等しく,山と山,谷と谷とが重なる条件は,δ21=2mπ(m=0,1,2,……)であり,このとき重ね合わせた光の強度は個々の強度の4倍となる。逆に山と谷とが重なるのはδ21=(2m+1)πのときであり,強度は0となる。光線に沿って測った長さをd,媒質の屈折率をnとするとき,ndを光路程,同一点から発した二つの光が別の径路を通って再び合するまでの光路程の差n2d2-n1d1を光路差という。位相差は光路差とδ21=(2π/λ0)(n2d2-n1d1)なる関係にある(ただし,媒質の境界などで位相の跳びがあれば,その差も含める)。
光路差の変化により生ずる強度の明暗を干渉縞という。光の場合,干渉性のきわめてよいレーザーを除けば,同一の光源の同一点から放出される光を分け,光路差があまり大きくない範囲でそれらを重ね合わせるのでなければ干渉縞はできない。ひとつながりの波を波連というとき,光源の1点からは相互に位相の関係がまったく不規則なきれぎれの波連が放出され,観測される光は,光源の異なる点から放出されるこのような波連の多数の重ね合せであるからである。一つの波連の長さは通常1m以下,継続時間にして3×10⁻9秒程度で,この分だけ振動数が不確定となり,スペクトル線の自然幅の原因になる。光の干渉する程度が悪くなると,位相差δ21はひんぱんかつ不規則に変化するようになり,観測される干渉縞は検出器の応答時間内の平均となる。干渉縞のコントラストから,光がどの程度干渉するか(これを可干渉性という)を知ることができる。また,最近の光検出器は応答時間が速く,波連の継続時間と同程度であるから,光の強度の相関から可干渉性を求めることができる。広がった光源の近くでは,ある場所の光とそのすぐ隣の光とは,光源の異なる点から出る波連の重ね合せ方が異なるので,ほとんど干渉しない。しかし,遠く離れ,光源を見込む角が小さくなれば,同じ隣合せの場所で波連の重ね合せは類似になり,そのため同じ光源から放出される光でも,光源から遠くでは干渉性がよい光になる。
回折
回折は,光が遮光板のうしろ側,すなわち影となる部分にまわり込む波動に特有な現象である。しかし,光の波長が短いため一般には目だたず,光は,1点から他の1点へ進むときには,それに要する時間が最小となるような径路を通るというフェルマーの原理に従って直進するようにみえる。フェルマーの原理は波長が0の極限で厳密に成り立ち,波長が有限のとき,焦点のように光が密集するところ,および影との境のように振幅が急激に変わるところを除いて正しい結果を与える。回折はしたがってフェルマーの原理の適用範囲から除かれたところで著しい。ホイヘンスの原理から,ある点Qにおける波動u(Q)は,その点を囲む閉曲面σ上の波動の値から一意に決まる。回折光の強度分布はこのことを数式化したキルヒホフの式,
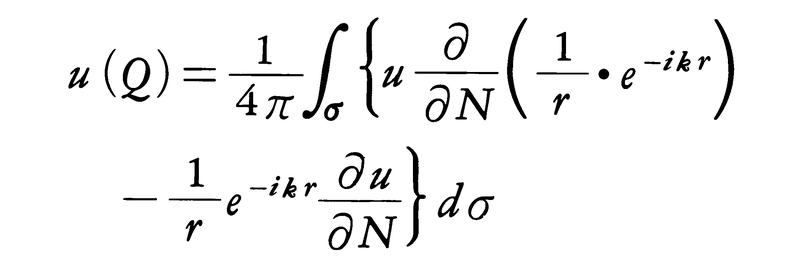
から求められる。ここにk=2π/λ0であり,Nは閉曲面に立てた内向きの法線,rは点Qより測った閉曲面上の点までの距離である(図2)。この閉曲面を遮光板に沿ってそのうしろ側にとれば,光が入射するところは遮光板の開口部分のみであるから,積分は開口部分について行えばよい。
光源と観測点とが遮光板の開口部分から有限の距離にある場合をフレネル回折,無限遠にある場合をフラウンホーファー回折という。レンズに平面波を入射するとき,光は1点に集まらず広がってしまうが,これはレンズの直径を開口とするフラウンホーファー回折のためであり,焦点面においては中心がもっとも明るく,光の強度は円環状に分布し,明暗が交互の回折像が生ずる。第1の暗環の半径は,レンズの直径と焦点距離をDおよびfとして1.220fλ0/Dで与えられる。レンズによって星など,無限遠にある二つの点光源をその焦点面に結像させたとき,一方の点光源のフラウンホーファー回折像の第1暗環より外側に,他方の点光源の像の中心が位置すれば,二つの像は区別できるので,二つの点光源が分解できたという。口径が大きくf/Dの値が小さい明るいレンズのほうが,像を分解する能力(分解能)が大きい。たてに長い開口を例にとって回折の強度分布を説明すると,中心のもっとも明るい部分は開口のすべての部分からの光がほとんど同じ位相で重ね合わされたところ,最初の暗部は開口の長さの半分だけ離れた開口上の2点からの光の光路差が半波長で,開口の上半分からの光と,下半分からの光とが干渉して消えてしまうところであり,第2の明るい部分は開口を三等分して,そのうちの二つを通る光が干渉して消し合い,残り一つを通る光で光の強度が決まるところである。
物体によるフレネルの回折波に,この光とよく干渉する平行光を参照光として重ね合わせて干渉縞を作り,写真乾板に記録したものをホログラムhorogramという。ホログラムに平行光を入射すると,直進する透過光のほかに,先ほどのフレネルの回折波が出てくる。ホログラムに光の波動が位相まで含めて記録されていたわけである。ホログラムより再生される回折波を目で受ければもとの物体が見え,立体感もある。再生される波動を別の光と干渉させることもでき,また記録と再生とに異なる波長の光を使って,像の拡大や縮小も行える。このような回折波の記録と再生の技術を総称してホログラフィーという。
光の放出と吸収
19世紀の終りから20世紀の初めにかけて,それまでの力学と電磁気学とでは,原子の性質を説明しつくせないことが明らかとなった。とくに物質の光学的性質はその代表的な例である。原子や分子はそれぞれ固有の光スペクトルをもち,水素原子のスペクトルなどには顕著な規則性のあることが見いだされた。このことは前期量子論によって説明が与えられたが,その端緒となったのはM.プランクが黒体放射のスペクトルを説明するために用いたエネルギー量子の考え方である。彼は放射(電磁波)とエネルギーをやりとりして平衡状態になっている空洞の壁を振動子の集合とみなし,この振動子のエネルギーが,エネルギー量子hνを単位としたとびとびの値しかとれないとしたのである(プランクの量子仮説)。これに対しアインシュタインは振動数νの放射そのものがエネルギー量子hνから構成されているとし,光(電磁波)はエネルギーhνをもつ粒子としてふるまうと考えれば光電効果が説明できることを示した(光量子仮説)。そしてこの光量子仮説を原子構造にとり入れることによって,N.H.D.ボーアは,原子の定常状態のエネルギーはとびとびの値しかとらず,原子がエネルギー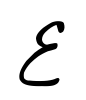 2の定常状態から
2の定常状態から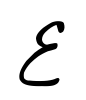 1(
1(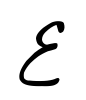 2>
2>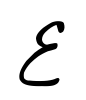 1)の定常状態へ遷移するとき,hν=
1)の定常状態へ遷移するとき,hν=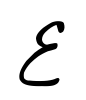 2-
2-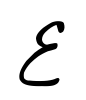 1なる振動数νの光を放出するとして,原子スペクトルの規則性に説明を与えたのである。
1なる振動数νの光を放出するとして,原子スペクトルの規則性に説明を与えたのである。
自然放出と誘導放出
物質からの可視光や紫外光の放出は,通常,原子内電子の定常状態間の遷移による。高いエネルギーの定常状態にある原子は,より低いエネルギーの定常状態に自発的に遷移するので,このような機構による光の放出は自然放出と呼ばれる。光が放出される機構には,このほかに誘導放出がある。入射光の強度に比例して光の放出が起こる現象で,レーザーはこれを利用している。誘導放出の光は入射光と同じ偏光,同じ進行方向であるが,自然放出の光はどんな偏光と進行方向の光であってもかまわず,単位時間当りに自然放出を生ずる遷移の起こる確率をA,一方,誘導放出の場合のそれをBとすると,
A=(8πhν3/c02)B
という関係がある。ここにhνc0は光子1個による光の強度,8πν2/c03はνとν+dνまでの振動数をもつ光が単位体積中でとり得る偏光と進行方向との種類の数である。
二つの定常状態をもつ原子からなる物質と,その差のエネルギーに相当する振動数の光とが共存している系は,原子が低いエネルギーの定常状態にあってエネルギーを光がもっている状況と,原子が高いエネルギーの定常状態にあってエネルギーを主として原子がもっている状況との間を往復する。光が外部に放出されてスペクトルに幅が生じたり,原子が外部からのかく乱を受けて定常状態間のエネルギー差に幅ができたりすると,この往復過程は中断され,このとき,原子がもっているエネルギーは光の吸収によって得たものである。
電気双極子相互作用
光と物質との相互作用は,物質内荷電粒子の加速に起因する。そのなかで主たるものは電気双極子相互作用である。光の電場によって物質の電気双極子モーメントの振動が励起されれば吸収が起こり,電気双極子モーメントがみずから振動すれば光が放出される。人工的な電気双極子の例は電波を放出する送信所のアンテナである。振動数νで振動する電気双極子モーメントPから単位時間に放出される電磁波のエネルギーは(4π2μ0/3c0)ν4|P|2である。アンテナに流す電流の振動数は光の振動数ほど大きくないが,赤外線の振動数は分子振動,可視光の振動数は原子内電子の運動による電気双極子モーメントの振動数の領域に含まれる。短波長の紫外線は荷電粒子を人工的に加速して発生させる。電子シンクロトロンなどの加速器では磁場によって電子の軌道を曲げるが,このときの加速度によって軌道の接線方向へ,紫外線を中心とする連続スペクトルの軌道面に平行な偏光が放出される。これをシンクロトロン放射といい,この光の発生は加速器の性能を限定する因子であるが,最近は,光源として積極的に利用されている。
執筆者:三須 明
光と文化
光の思想史
光は古来文学,哲学,宗教において比喩として用いられる。地上の明るい世界と地下の暗い冥府が光と闇の対比で表される。光は生命の充実,清浄さ,自由,希望,喜び,神々の至福の世界を表し,また見る働きの媒体,見られた対象,事象の洞察,世界認識とその力を表す。光は神的なものの顕現,臨在であり,それによって霊界,精神界が自覚され,自己認識が生ずる。アレテイアalētheia(真理)とは〈隠れなきこと〉の意であり,真理と光は同一視される。光を重視したパルメニデスとプラトンの哲学およびそれを受け継いだ形而上学の伝統は〈光の形而上学〉と呼ばれる。そこでは光は真なる存在の比喩ではなく,むしろ真なる存在が明るいものであり,万物がそこから発生し,また人々はその光に照らされて真なる存在へと還帰する。光は突如輝き出るが,それに照らされることは単なる主観的体験ではなく,対象知の獲得とであり,これは神秘的というよりも合理的,存在論的な知の成立である。
死者の祭礼において,光は死者にまといつく闇と悪鬼を追い払って蘇生させえる。これは神の顕現の結果であり,個人的な照明ではなくて,闇から光への移行ないし交替である。ギリシアの神秘宗教は,この意味での光の入射を〈エランプシスellampsis〉と呼んだ。古来東方では光は形而上的なものではなくて自然的なものであり,太陽,光,生命,救いは一つであった。エジプトやイランやバビロニアでも同様であるが,シュメールの〈ヨブ物語〉には,光のなかで闇にかこまれるという経験がしるされている。後期のアベスターとゾロアスター教の成立によって初めて光と闇の二神が出現する。
旧約聖書では光は神の実体ではなく関係を表す。光は創造によって与えられたものであり,神は光と闇の主である(《アモス書》5:8)。終末の日であるヤハウェの日は暗いといわれる(同5:18)。ユダヤ教のクムラン教団では〈光の子〉と〈闇の子〉との戦いがいわれるが,この二元論をゾロアスター教に関係づけるのは正しくない。ここでは光は物象ないし領域ではなくて道であり,決断によって受け取られるものである。新約聖書では光は比喩と実体との両方でいわれる。パウロはコリント教会で神秘宗教と対決したさい,光を神秘とする考えを排して,キリスト再臨における新しい創造と復活のできごとに結びつけた。《ヨハネによる福音書》ではイエスは〈世の光〉であり,昼間働くといわれる。光と闇の対立は神話的ではなく,〈善き業(わざ)〉と〈悪しき業〉との対比でいわれる。イエスはまた〈啓示の光〉であり,これに面して信仰と不信仰とが二元論的にではなく決断的に分けられる。
ヘレニズムにおいてヘルメス文書,マンダ教,マニ教のグノーシス的二元論では光は形而上的であると同時に自然的であり,太陽や月がそのまま真の光とされる。この混合のゆえに,救いは罪からの解放ではなく,二つの世界の戦いとなり,変化や運動ではなく分離によって光を自分のものとしたとき救いが得られる。他方,神秘宗教と哲学(とくに新プラトン主義)では戦いではなく上昇がいわれる。魂は照明により光の世界へ昇り,かつ変容して光の魂となる。ウェルギリウスとオウィディウスにもこれがみられる。プロティノスはプラトンと違って,神の模倣ではなく神となることをいい,理性認識の対象たるイデア界をも超えて魂が光となることをいう。その光は現実の光ではないので,絶対の闇が同時に絶対の光だといわれる。これをうけつぐ中世の神秘主義は黙示的歴史観と結びついて〈ルネサンス(再生)〉(神的な〈光の時代〉の到来)の観念を生んだ。18世紀の〈Enlightenment(啓蒙)〉は文字どおり〈エランプシス〉の訳であるが,神秘主義の伝統は消えて,神的光の入射ではなく自然的理性の開示であり,ルネサンスにはまだなされていなかった脱魔術化と世俗化をめざすものであった。
→光の形而上学
執筆者:泉 治典
美術における光
西洋絵画では,現実世界におけると同様に対象を照らし出す光の表現は,古典古代と近世以降とに認められる。ヘレニズムと古代ローマの画家は,光源を想定し,これに応じて対象の明部と暗部を描きわけ,投影や表面の反射を表し,光を受けて輝く突出部を示す白のタッチ(ハイライト)を置くことを知っていた。ルネサンス絵画においてはこの面でも〈古代の復活〉が起こっている。当初は1300年前後のジョットの壁画に見られるように,画中の対象の照らされた部分と陰になった部分を区別して形と立体感を強調するにとどまるが,15世紀に入ると,地面や壁面への投影も描かれて空間の広がりとその中での立体の確固たる存在感が暗示されるようになる。首尾一貫した明暗の配分により,描かれた世界に自然なまとまりが与えられたばかりでなく,マサッチョ作のサンタ・マリア・デル・カルミネ教会ブランカッチ礼拝堂壁画(1420年代後半)や,ファン・アイク兄弟作の《ヘント祭壇画》(1432)中の〈聖告〉のように,絵画空間を照らす画面外の光源を作品のある現実空間の光源(窓)に一致させて,迫真的な光の効果を高めることもあった。また,とくに15世紀のフランドルでは,事物の表面の反射の差異によるさまざまな材質感の描出が追求されている。このような写実的な光の表現は,線遠近法による合理的空間表現とともに,ルネサンスから19世紀に至る西洋絵画の基本的特色をなす。天候や時刻が識別できる風景画が発達し得たのも,このような光の表現があればこそである。
これに対し中世美術においては,光はきわめて重要な要素ではあるものの,そのあり方は古代および近世と著しく異なる。中世美術の中枢を占める教会堂建築では,古代に比べて内部空間が格段の重要性を得たのに伴い,金地とガラス片の輝かしいモザイク,戸外の白色光を色とりどりの光に変えるステンド・グラスが,聖性を象徴する超現実的な光でこれを満たすようになった。一方,中世絵画には,古代と近世の写実的光を基準にすれば,光は存在せず色彩あるのみということになるが,中世には独自の光があることに注目しなければならない。つまり,古代とルネサンス以降の絵画の光が対象を外から照らし出す光であるのに対し,中世絵画,とくに写本画やステンド・グラスの光は絵画そのものから発するのである。この効果は,金泥や金箔,鮮明な色面,色ガラスを通してさし込む光などにより達成されている。このような中世美術の光は,地上における聖性の顕現という象徴的意味を担っている。
ただし,光の象徴性は非写実的様式とのみ結びつくわけではない。ルネサンスの写実的傾向がさらに強まったバロックの絵画においても,カラバッジョの宗教画にみられるように,一見現実的な光が現世の闇に輝く神的なるものを象徴していることがある。レンブラントは宗教画のみならず肖像画においても,内面性を表現する手段として光を用いた。バロック絵画ではまた強烈な明暗対比による劇的効果も追求され,そのために画中に光源として人工照明を描くことも好まれた。
19世紀半ばまで絵画の中の光は,自然光として表されている場合でも,アトリエ内で再現されたものであった。これに対し,印象派は実際に屋外に赴き,陽光下の輝かしい色彩を画布にとらえようとする。ところが,陽光を構成する光は集まれば白色光になるが,物質である絵具は混ぜるにつれて明るさを失う。そこで案出されたのが,陽光を反射する対象の色彩を混色によらず基本色の並列で示すことにより,明るさを保持しつつ見る者の網膜上に中間色を喚起するというやり方であった(ディビジヨニスム,点描主義)。西洋絵画における写実的な光の表現の探求は,ここでその極限に達したといえる。
彫刻は,浮彫の芸術的魅力が表面にあたる光の生み出す微妙な明暗の効果に負うところ大であるのを認めるにせよ,あくまでも外在的なものとしての光とのかかわりしかもたない。しかしその中でもバロックの彫刻は,ベルニーニ作の《聖テレサの法悦》のように,聖性の暗示,劇的効果の達成のため,周囲の現実の光を十二分に活用している。
最後に日本と中国について付言すれば,仏画や水墨山水画の場合,対象を隈取って立体感を暗示する一種の陰影法があるものの,具体的光源は想定されておらず,むしろ西洋絵画におけるような光の表現がないことが日本・中国美術の一特色であろう。ただ,桃山から江戸初期の金碧障壁画の金地の広がりは,金箔という物質に翻訳された光そのものであり,日本美術において光の効果が意識的に追求された稀有(けう)な例といえるだろう。
→陰影法 →明暗法
執筆者:高橋 裕子
 〈コウ〉
〈コウ〉 〈ひかり(びかり)〉「稲光・七光」
〈ひかり(びかり)〉「稲光・七光」


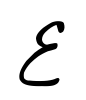 =hνのエネルギーと,向きが光の進行方向で大きさがp=h/λ0の運動量をもつ粒子としてふるまい(hは
=hνのエネルギーと,向きが光の進行方向で大きさがp=h/λ0の運動量をもつ粒子としてふるまい(hは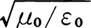 となり,また光速度c0は,
となり,また光速度c0は,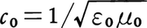 で与えられる。光の強度は
で与えられる。光の強度は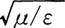 光の速さは
光の速さは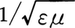 となるが,光の振動数はきわめて大きいので,通常の物質ではμ=μ0としてよく,
となるが,光の振動数はきわめて大きいので,通常の物質ではμ=μ0としてよく,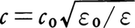 と表せる(ただし,この場合εは光の振動数に依存すると考えなければならない)。
と表せる(ただし,この場合εは光の振動数に依存すると考えなければならない)。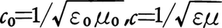 またほとんどの場合μ0=μとしてよいことから,
またほとんどの場合μ0=μとしてよいことから,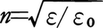 で与えられることになる。ただしこのnの値は光の振動数によって変化し,とくに気体の場合,分極率との関係は
で与えられることになる。ただしこのnの値は光の振動数によって変化し,とくに気体の場合,分極率との関係は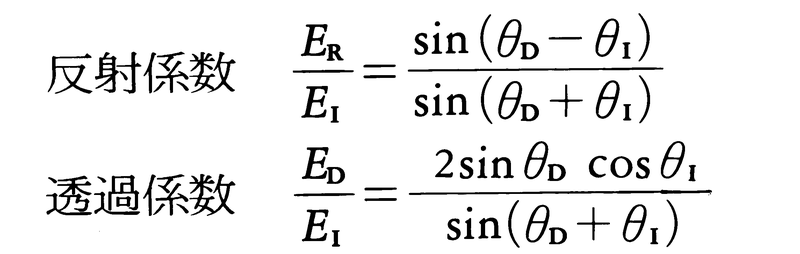
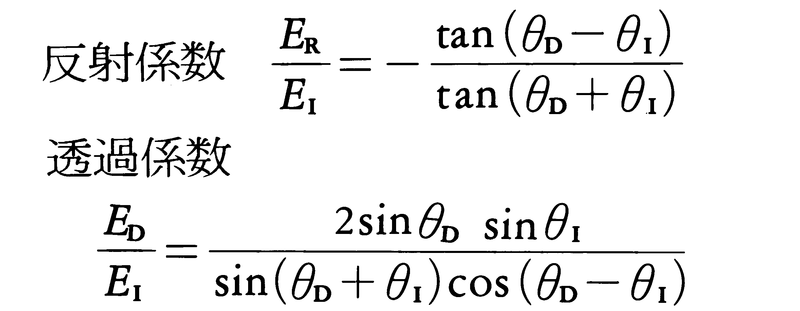
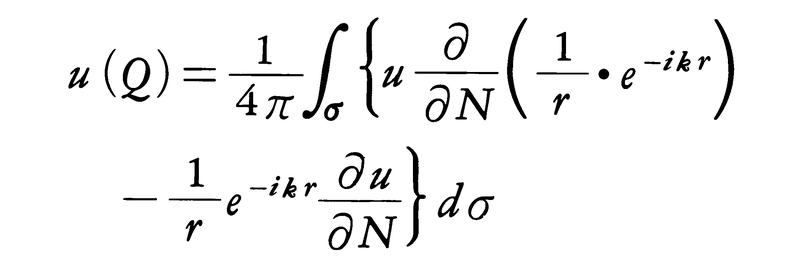
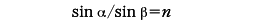
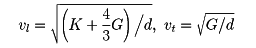













 (望)・先・
(望)・先・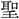 (聖)・
(聖)・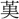 (かん)、また聞の初文など、すべてその機能を上に掲げるもので、同じ形式の造字法である。殷の金文に光の下部を女の形に作るものがある。〔説文〕十上に「
(かん)、また聞の初文など、すべてその機能を上に掲げるもので、同じ形式の造字法である。殷の金文に光の下部を女の形に作るものがある。〔説文〕十上に「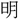 なり」とあり、光明の意とする。金文の〔令彝(れいい)〕に「用(もつ)て
なり」とあり、光明の意とする。金文の〔令彝(れいい)〕に「用(もつ)て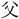 丁(父の
丁(父の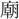 号)を光(かがや)かさん」、〔毛公鼎〕「
号)を光(かがや)かさん」、〔毛公鼎〕「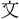 武の耿光(かうくわう)」、〔晋姜鼎(しんきようてい)〕「
武の耿光(かうくわう)」、〔晋姜鼎(しんきようてい)〕「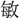 (いそ)しみて厥(そ)の光剌(くわうれつ)に揚(こた)へん」のように、光栄・光烈の意に用いている。
(いそ)しみて厥(そ)の光剌(くわうれつ)に揚(こた)へん」のように、光栄・光烈の意に用いている。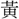 (黄)を古文光に従うとするが、
(黄)を古文光に従うとするが、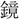 (鏡)kyang、影yang、曠khuangも、みなこの系列に属し、光景・光耀に関する語である。
(鏡)kyang、影yang、曠khuangも、みなこの系列に属し、光景・光耀に関する語である。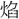
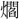
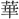
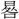
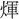
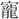
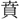
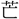
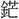
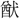
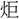 光・虚光・鏡光・暁光・旭光・極光・蛍光・景光・
光・虚光・鏡光・暁光・旭光・極光・蛍光・景光・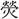 光・月光・剣光・顕光・孤光・弧光・後光・紅光・高光・国光・金光・採光・三光・散光・射光・遮光・赤光・寂光・珠光・春光・曙光・昭光・消光・晶光・燭光・晨光・新光・水光・垂光・翠光・瑞光・清光・晴光・精光・雪光・川光・閃光・争光・大光・池光・昼光・
光・月光・剣光・顕光・孤光・弧光・後光・紅光・高光・国光・金光・採光・三光・散光・射光・遮光・赤光・寂光・珠光・春光・曙光・昭光・消光・晶光・燭光・晨光・新光・水光・垂光・翠光・瑞光・清光・晴光・精光・雪光・川光・閃光・争光・大光・池光・昼光・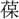 光・明光・夜光・幽光・
光・明光・夜光・幽光・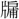 光・余光・妖光・容光・揚光・陽光・流光・
光・余光・妖光・容光・揚光・陽光・流光・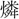 光・霊光・烈光・露光・和光
光・霊光・烈光・露光・和光